КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ ПРОЦЕССОВ КОНТАКТНОГО ВЗАИМОДЕЙСТВИЯ ИНДЕНТОРА С ИССЛЕДУЕМЫМ ОБЪЕКТОМ ПРИ ДИНАМИЧЕСКОМ ИНДЕНТИРОВАНИИ

Одним из перспективных методов исследования механических характеристик материала является метод динамического индентирования (ДИ). Основными преимуществами данного метода являются достоверно определения механических характеристик материала и использование портативного оборудования для исследования крупногабаритных объектов. В основе данного метода лежит непрерывная регистрация процесса ударного локального контактного взаимодействия индентора (в основном в форме шара) с испытываемым материалом, а именно регистрация текущей скорости движения индентора. На начальном этапе проектирования портативного прибора для измерения твердости материала методом динамического индентирования, в зависимости от того какой материал будет исследовать разрабатываемый прибор, необходимо знать скорость с которой будет падать индентор на исследуемый материал, геометрические параметры самого индентора, величину остаточной деформации в исследуемом материале и другие. В этом случае наибольший интерес представляет компьютерное моделирование процесса контактного взаимодействия индентора с исследуемым материалом. Данный метод позволят устранить возможные ошибки еще на этапах проектирования измерительного прибора.

Для получения быстрых и наглядных результатов подобные задачи решаются с помощью различных программных систем, таких как ANSYS, LS-DYNA, COMSOL Multiphysics, ABAQUS и др.

Рисунок 1. Перспективная модель прибора для динамического индентирования

Эти программы основаны на методе конечных элементов, который широко используется для решения задач механики деформируемого твердого тела. Анализ вышеперечисленных программных комплексов показал, что наиболее приемлемой для решения взаимодействия является программа ANSYS. Поставленная задача решалась с помощью модуля ANSYS Mechnical. Данный модуль используется для решения задач механики деформируемого тела, с использованием линейных, нелинейных и динамических исследований.

Таблица 1.

Механические характеристики материалов

В качестве результата моделирования в статье приведены результаты моделирования контактного взаимодействия индентора с исследуемым материалом. Исходные данные материалов индентора и исследуемого материала приведены в таблице 1.

Условно процесс моделирования в программном комплексе ANSYS можно поделить на следующие этапы (рис. 2) [2]:

1.  Выбрать модель поведения материалов, задать исходные материалы, которые будут использоваться при моделировании.

2.  Построить геометрию модели в плоскости или в трехмерном виде.

3.  Создать конечно-элементную сетку.

4.  Задать типа контактного взаимодействия, установить граничные условия.

5.  Задать силы, которые будут действовать на всю систему либо на его отдельные элементы.

6.  Запустить решатель.

7.  Анализ и обработка полученных данных.

Рисунок 2. Этапы инженерного анализа при моделировании в ANSYS

Выбор характеристик материала производился в отдельном разделе ANSYS – “Engeneering Data”. В данном разделе расположены библиотека материалов в котором содержатся некоторые стандартные материалы с уже подобранными для них механическими характеристиками и свойствами. Кроме того, имеется возможность создать свою библиотеку материалов при отсутствии нужного материала в списке библиотеки. В нашем случае для задания линейных свойств материала необходимо ввести значения коэффициента Пуассона модуля упругости. Для моделирования упрочнения в программном комплексе используется законы кинематического и изотропного упрочнения, при этом в том же разделе задается предел прочности и касательный модуль. Необходимые данные для индентора и исследуемого материала были взят из таблицы 1.

При построении геометрии, для оптимизации расчета и уменьшения времени решения задачи применялось осесимметричная постановка с двумерным типом анализа. Геометрия моделей стоится в отдельном разделе программного комплекса «Geometry» там же можно определить тип повеления “Axisymmetric”.

Следующим этапом необходимо задать контактную пару между материалом и индентором. В данной задаче поверхность индентора задавалась как Contact Body, а исследуемого материала как Target Body. Так же для моделирования деформацй материала созадавалась конечно-элементная сетка. Для более точного расчета деформации конечно-элементная сетка была изсельчена в зоне контакта индентора с материалом. Поскольку деформации индентора по сравнению с материалом минимальны генерация сетки для индентора выбиралась по умолчания. С результатом построения конечно-элементной представлен на рисунке 3.

Рисунок 3. Генерация сетки

В разделе Model устанавливаются граничные условия и определяются силы, которые действуют на системы в целом либо на некоторые элементы конструкции [1]. При моделировании данного процесса, для ограничения исследуемого материала, она фиксировалась по нижней грани. На всю систему действует ускорение свободного падения 9,81 м/с². При моделировании контактного взаимодействия значения скорости индентора брались равными 1,25 м/с и 1,5 м/с. Направления скорости индентора была бралась вниз по направлению оси симметрии. В этом разделе так же устанавливается время моделирования и задается минимальный и максимальный шаг по времени.

В разделе Solution выбирается типа решателя. Для расчета упругих и пластических деформаций выбираются “Equivalent Plastic Strain” и “Equivalent (von-Mises) Strain” соответственно. Так же для определения зависимости «Контактное усилие – Глубина внедрения» требуется скорость индентора. Для расчета изменения скорости индентора применяется тип анализа “Directional Velocity” [3].

Результаты полученных при моделировании контактного взаимодействия отображаются в разделе Results. На рисунке 4 представлены распределения упругих и пластически деформаций при моделировании контактного взаимодействия с индентором. При этом диаметр индентора равен 2 мм, а ее скорость составляет 1,5 м/с.

Рисунок 4. Упругие и пластические деформации при скорости 1,5 м/с

Так же были проведены подобные моделирование при скорости 1,25 м/с, исследуемый материал – сталь 45, диаметр индентора 1,5 мм. Результаты представлены на рисунке 5.

Рисунок 5. Упругие и пластические деформации при скорости 1,25 м/с

Используя данные полученные при моделировании процесса контактного взаимодействия была получены зависимость «Контактное усилие – глубина внедрения индентора в исследуемый материал». Полученная зависимость (рис. 6) может быть использована для определения основных механических свойств материала.

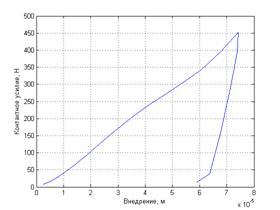
Рисунок 6. Зависимость «Контактное усилие – внедрение»

Список литературы:

1. Давыдов А.Н. Решение статических задач с использованием пакета программ ANSYS. Самара: СамГТУ; 2014. – С. 18–19.
2. Клебанов Я.М., Фокин В.Г., Давыдов А.Н. Современные методы компьютерного моделирования процессов деформирования конструкций: учеб. пособие. – Самара: СамГТУ, 2004. – 100 с. – ISBN 5-7964-0553-5.
3. Лукьянова А.Н. Моделирование контактной задачи с помощью программы ANSYS: учеб.-метод. пособие. / А.Н. Лукьянова. – Самара; СамГТУ, 2010. – 52 с.