РАЗРАБОТКА АЛГОРИТМА ПО ОПРЕДЕЛЕНИЮ КОЭФФИЦИЕНТОВ ЛОГИСТИЧЕСКОГО УРАВНЕНИЯ, ОПИСЫВАЮЩЕГО ЗАВИСИМОСТЬ ПЕРИОДА МАКРОЛОКАЛИЗАЦИИ ПЛАСТИЧЕСКОЙ ДЕФОРМАЦИИ ОТ РАЗМЕРА ЗЕРНА С УЧЕТОМ ИЗМЕНЕНИЯ ГЕОМЕТРИЧЕСКИХ ПАРАМЕТРОВ ОБРАЗЦОВ
Секция: 7. Материаловедение

XXV Студенческая международная заочная научно-практическая конференция «Молодежный научный форум: технические и математические науки»
РАЗРАБОТКА АЛГОРИТМА ПО ОПРЕДЕЛЕНИЮ КОЭФФИЦИЕНТОВ ЛОГИСТИЧЕСКОГО УРАВНЕНИЯ, ОПИСЫВАЮЩЕГО ЗАВИСИМОСТЬ ПЕРИОДА МАКРОЛОКАЛИЗАЦИИ ПЛАСТИЧЕСКОЙ ДЕФОРМАЦИИ ОТ РАЗМЕРА ЗЕРНА С УЧЕТОМ ИЗМЕНЕНИЯ ГЕОМЕТРИЧЕСКИХ ПАРАМЕТРОВ ОБРАЗЦОВ
Локализация пластической деформации металлов и сплавов является существенным, а часто – определяющим фактором многих технологических процессов, связанных с формоизменением. В ходе многочисленных экспериментов [1] было установлено, что длина автоволны локализованной деформации металлов и сплавов зависит от размера зерна по логистическому закону. Данная зависимость была установлена аналитически, значение коэффициентов для образцов с геометрическими параметрами 2×10×50 мм были получены с помощью численной обработки экспериментальных данных. Помимо этого ранее было установлено, что существует зависимость изменения периода макролокализации пластической деформации при изменении геометрических параметров образцов (в частности толщины). Таким образом, представляет интерес разработка программного приложения по автоматизированному определению периода макролокализации в зависимости от размера зерна с учетом изменения геометрии образца и установления зависимости коэффициентов логистического уравнения от изменения геометрии.
Материалом для исследования служил поликристаллический алюминий чистоты 99.85 wt % [3]. Плоские образцы с размерами рабочей части 2×10×50 мм или 5×10×50 мм растягивались вдоль длинной оси на машине Instron-1185 со скоростью ![]() =6,67*10-5s-1 при 300 K с одновременной записью диаграммы.
=6,67*10-5s-1 при 300 K с одновременной записью диаграммы.
Одновременно с проведением механических испытаний, методом двухэкспозиционной спекл-фотографии регистрировались картины локализации, т. е. пространственно-временные распределения очагов локализации пластического течения [1].
В результате съёмки и расшифровки спеклограммы было получены данные о распределении компоненты тензора пластической дисторсии ![]() xx по образцу.
xx по образцу.
На рисунке 1 приведена картина типичного распределения компоненты тензора пластической дисторсии ![]() xx по образцу.
xx по образцу.
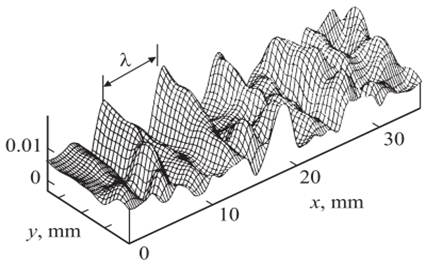
Рисунок 1. Пример картины распределения компоненты тензора пластической дисторсии ![]() xx по образцу
xx по образцу
Расстояние между максимумами является периодом макролокализации пластической деформации λ. Зависимость периода макролокализации от размера зерна для образцов с геометрическими параметрами 2×10×50 мм (толщина образца × ширина образца × длина рабочей поверхности) представлена на рисунке 2.
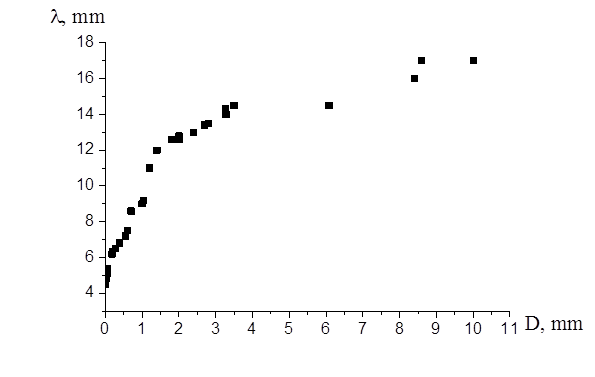 Рисунок 2. Зависимость λ(D) при толщине образца 2 мм, ширине 10 мм, длине рабочей поверхности 50 мм
Рисунок 2. Зависимость λ(D) при толщине образца 2 мм, ширине 10 мм, длине рабочей поверхности 50 мм
На рисунке 2 приведена зависимость пространственного периода макролокализации пластической деформации от размера зерна, для участка с параболическим законом деформационного упрочнения и соответствует участку деформационной кривой при 8—10 % от общей деформации. При общей характеристике полученной зависимости отметим, что при увеличении размера зерна, значение пространственного периода (длина волны) возрастает. Однако при достижении размера зерна, величины сравнимой с поперечником образца, темп прироста замедляется. При достижении определенного размера зерна, величина пространственного периода становится постоянной.
Анализ данной зависимости показывает, что для исследованного диапазона значений D функция λ(D) имеет два предельных участка: при D ≤ 50 мкм длина волны λ ~ eD, при D ≥ 2,5 мм λ → λ0 ≈ 15 мм (λ0 — предельное значение длины волны локализованной деформации в алюминии). В промежуточной области эти участки плавно переходят один в другой. Численная обработка данных показала, что они достаточно точно могут быть аппроксимированы уравнением [2]:
![]() (1)
(1)
Это уравнение является решением дифференциального уравнения, связывающего величины l и D,
![]() (2)
(2)
Здесь a и b — положительные размерные константы (размерность а — м-1, размерность b — м-2). Квадратичный член bλ2 в правой части (2) учитывает связанное с ограниченностью размеров образца замедление прироста λ в области больших зерен.
Решением дифференциального уравнения (2) является логистическая функция (1), в которой λ0= a/b, а C — безразмерная постоянная интегрирования. Можно сказать, что уравнение (1) с удовлетворительной точностью описывает совокупность полученных экспериментальных данных для зависимости λ(D) в широком интервале значений D.
Численная обработка опытных данных по уравнению (2) позволяет определить значения постоянных а = 1,37 мм-1 и b = 8,8×10-2 мм-2 в уравнениях (1) и (2). Величинам с размерностью длины 1/a ≈ 0,73 мм и ![]() ≈3,4 мм можно придать простой геометрический смысл: они близки к одной трети толщины и ширины использованных образцов соответственно.
≈3,4 мм можно придать простой геометрический смысл: они близки к одной трети толщины и ширины использованных образцов соответственно.
Заметим, что при использовании толстых образцов (5 мм) соответствующие точки лежат выше общей закономерности, что косвенно подтверждает сделанное заключение.
Основываясь на вышеизложенном, был разработан алгоритм, позволяющий определять значение периода макролокализации пластической деформации при изменении размера зерна для образцов с геометрическими параметрами 2×10×50 мм. Данный алгоритм положен в основу разрабатываемого программного приложения.
Заключение.
Результаты работы алгоритма хорошо согласуются с экспериментальными данными с учетом коэффициента корреляции.
Планируется использование разработанного алгоритма для дальнейшего моделирования решения логистического уравнения Ферхюльста при изменении геометрических параметров образцов.
Список литературы:
1. Зуев Л.Б., Данилов В.И., Баранникова С.А. Физика макролокализации пластического течения. — Новосибирск: Наука, 2008. — 327 с.
2. Мэрди Дж. Математическое моделирование. — М.: Мир, 1979. — С. 109—127.
3. Шмид Е., Боас В. Пластичность кристаллов, в особенности металлических. — М.: ГОНТИ НКТП, 1938. — 316 с.





