ДИАГНОСТИКА ЭЛЕКТРИЧЕСКИХ МАШИН В УСЛОВИЯХ СИЛЬНЫХ ИМПУЛЬСНЫХ ПОМЕХ НА ОСНОВЕ ИНС

Получены результаты, подтверждающие возможность использования нейронных сетей для идентификации и диагностики параметров электрических машин в условиях наличия сильных импульсных помех в измерительной системе. Предложена структура нейронной сети и способ подготовки тренировочного набора для ее обучения.

Ключевые слова: искусственная нейронная сеть (ИНС), идентификация, диагностика, электрическая машина.

Введение. Автоматизированные системы управления и диагностики электрических машин довольно уязвимы при работе в условиях реального промышленного предприятия. Различного рода импульсные помехи могут привести к появлению нежелательных сигналов от датчиков, в цепях связи и непосредственно в аппаратуре управления. Источниками импульсных помех в сетях является: включение или отключение потребителей энергии (электродвигатели, лампы накаливания и дневного света, компьютеры и др. аппаратура); включение и отключение цепей с большой индуктивностью (трансформаторы, пускатели и т. д.); аварийные короткие замыкания в сети и их последующее отключение защитными устройствами; включение и отключение электросварочных установок; источником импульсных помех является городской электрифицированный транспорт, включая метро, а также электрифицированные железные дороги.

Импульсная помеха может быть усилена системой управления и обратной связью, что может привести к некорректной работе или отказу работы аппаратуры управления. Наиболее эффективным способом обеспечения надежной работы современных автоматизированных систем управления и диагностики является введение интеллектуального отказоустойчивого управления (fault tolerant control (FTC)) [1]. Структура FTC показана на рисунке 1. В FTC объединены принципы управления, диагностики и возможность построения системы ресурсосберегающей эксплуатации при наличии некритических дефектов в ЭМ.

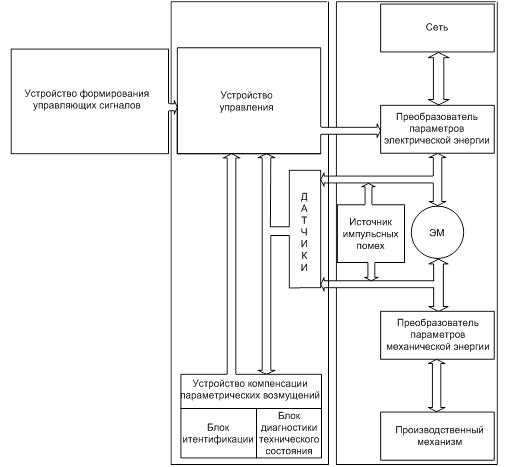
Рисунок 1. Структурная схема FTC

Одним из способов идентификации параметров электрических машин переменного тока является применение искусственных нейронных сетей [2]. Благодаря своим аппроксимирующим свойствам, искусственные нейронные сети позволяют проводить идентификацию на основе зашумленных данных с наличием сильных импульсных помех.

Целью исследования являлась оценка чувствительности нейросетевой идентификационной модели к импульсным помехам в обучающей выборке и входных сигналах.

Нейросетевая идентификация частоты вращения вала асинхронного двигателя.

Для анализа влияния импульсных помех на нейросетевую идентификацию проводилось исследование асинхронного двигателя с короткозамкнутым ротором. Экспериментальная установка включала сочлененные между собой и установленные на едином основании машину постоянного тока, машину переменного тока, маховик и преобразователь угловых перемещений. Для сбора и записи сигналов датчиков использовалась плата сбора данных PCI-6024E фирмы National Instruments. Для программирования платы сбора данных использовался пакет LabVIEW.

В ходе исследования были получены переходные характеристики фазных токов, напряжений и скорости вращения ротора двигателя при пуске, набросе и сбросе нагрузки и торможении двигателя. Примеры графиков переходного процесса показаны на рисунке 3.

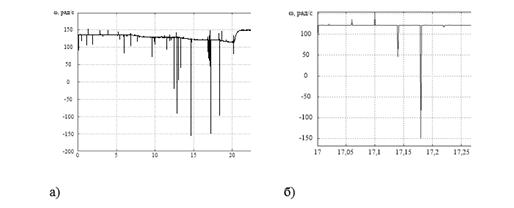
Рисунок 3. Характер изменения сигналов в канале измерения скорости: а) сигнал скорости при набросе и сбросе нагрузки; б) пример отдельных импульсов

На обучающей выборке, сформированной из полученных зашумленных данных, обучался нейроэмулятор. Для нейроэмулятора была выбрана рекуррентная искусственная нейронная сеть вида 17‑20‑1, функция активации — гиперболический тангенс. Входными величинами являлись текущие и задержанные единожды, дважды и трижды значения токов и напряжений двух фаз статора двигателя, выходной — частота вращения ротора двигателя. Сеть обучалась методом Левенберга-Марквардта [3]. Число циклов обучения: 100. Сеть формировалась и обучалась с использованием набора инструментов Neural Network Toolbox программного пакета MatLab.

Для оценки точности идентификации опытные данные были сглажены при помощи, взвешенной локальной квадратичной регрессии [4]. Сглаженные опытные данные приняты в качестве эталонных [5]. Графики сглаженных опытных данных и оценки скорости с использованием нейроэмулятора приведены на рисунке 5.

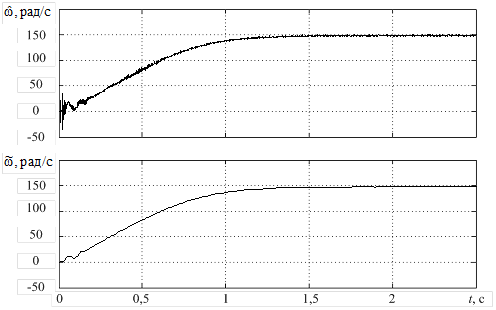
Рисунок 5. Графики сглаженных опытных данных и оценки частоты вращения ротора при пуске двигателя вхолостую

Среднеквадратическую погрешность измерения частоты вращения ротора двигателя в условиях сильных импульсных помех в измерительной системе предлагается определять по формуле:

,

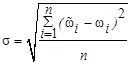где: σ — среднеквадратическая погрешность,  — сглаженная частота вращения ротора на шаге интегрирования i,  — определенная в ходе исследования частота вращения ротора на шаге интегрирования i, n — число шагов интегрирования.

Среднеквадратическая погрешность измерения при пуске двигателя вхолостую за 2,5 с составила 0,88 рад/с, при набросе и сбросе нагрузки за 25 с — 4,06 рад/с, при торможении за 6 с — 2,62 рад/с.

Среднеквадратическая погрешность оценивания частоты вращения ротора двигателя с помощью нейроэмулятора рассчитывается по формуле:

,

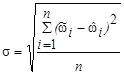где: σ — среднеквадратическая погрешность,  — сглаженная частота вращения ротора на шаге интегрирования i,  — оценка частоты вращения ротора на шаге интегрирования i, n — число шагов интегрирования.

Среднеквадратическая погрешность измерения при пуске двигателя вхолостую за 2,5 с составила 2,6 рад/с, при набросе и сбросе нагрузки за 25 с — 1,69 рад/с, при торможении за 6 с — 1,92 рад/с.

Следовательно, нейроэмулятор позволяет оценивать частоту вращения ротора асинхронного двигателя с достаточной точностью даже при значительной погрешности измерения.

Заключение.

Таким образом, искусственные нейронные сети дают возможность работать с зашумленными данными в измерительной системе FTC, избавляя от необходимости применения для защиты от помех промежуточных электронных фильтров или фильтрации с помощью специализированных математических методов, таких как регрессия, сглаживание, интерполяция и т. п.

Список литературы:
1.    Метод Левенберга-Марквардта — [Электронный ресурс] — Режим доступа: http://alglib.sources.ru/optimization/levenbergmarquardt.php, свободный, 13.05.2011.
2.    Осовский С. Нейронные сети для обработки информации: пер. с польск. — М.: Финансы и статистика, 2002. — 344 с.
3.    Тихонов А.Н. Методы решения некорректных задач: учебное пособие / А. Н.Тихонов, В.Я. Арсенин. — 3-е изд., перераб. и доп. — М.: Наука, 1986. — 286 с.
4.    Хардле В. Прикладная непараметрическая регрессия: пер. с англ. — М.: Мир, 1993. — 349 с.
5.    Mogens Blanke, Marcel Staroswiecki and N. Eva Wu. Concepts and Methods in Fault-tolerant Control // Tutorial at American Control Conference, June 2001.