РАЗРАБОТКА МЭМС — ЕМКОСТНОГО ЧУВСТВИТЕЛЬНОГО ЭЛЕМЕНТА АКСЕЛЕРОМЕТРА ГРЕБЕНЧАТОГО ТИПА

В качестве конструкции МЭМС чувствительного элемента акселерометра емкостного типа, предлагается рассмотреть гребенчатую структуру, представленную на рисунке 1, с продольным перемещением инерционной массы под воздействием ускорения.

Рисунок 1. ЧЭ МЭМС-акселерометра гребенчатого типа

Материалом для изготовления ЧЭ служит структура кремний на изоляторе (КНИ), основание из SiO₂ с нанесенным на него слоем стекла, которое впоследствии стравливается, для обеспечения зазора между инерционной массой и статором, поверх стекла расположен слой низкоомного кремния из которого вытравливается ротор. Модель ЧЭ представлена на рисунке 2.

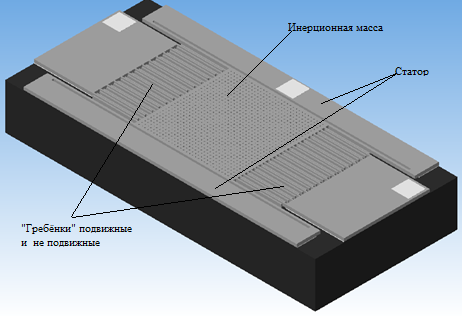
Рисунок 2. Модель ЧЭ акселерометра

«Инерционная масса, закрепленная на статоре, обладает способностью перемещаться влево-вправо под воздействием ускорения приложенного вдоль конструкции. В результате меняется расстояние между неподвижными и подвижными гребенками, а, следовательно, емкости образованных конденсаторов» [2]. При отсутствии внешнего ускорения емкости составят:

                                                                  (1)

где: ε₀ = 8,85∙10^-12 Ф/м — диэлектрическая постоянная;

N — число емкостей, образованных неподвижными и подвижными гребенками;

L_f — длина гребенки;

t — толщина гребенки;

d₀ — зазор между гребенками.

При появлении ускорения, направленного вдоль измерительной оси, меняется расстояние между гребенками на величину δ, а, следовательно, емкость будет равна:

                                               (2)

Для расчета конструкции ЧЭ воспользуемся типовым опорным элементом микромеханической системы, в нашем случае в качестве исходной модели будет использоваться схема с двухконсольной балочной опорой, показанной на рисунке 3, а, которую мы в дальнейшем изменим для полного соответствия конструкции разрабатываемого чувствительного элемента. Расчетная схема системы для исходной схемы приведена на рисунке 3, б. Эквивалентная система показана на рисунке 3, в.

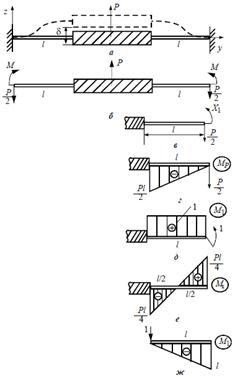
Рисунок 3. «Двухконсольная мостовая балочная опора: а — схема нагружения и деформации системы; б — расчетная схема; в — эквивалентная система; г — эпюра изгибающих моментов от действия реактивной силы P/2; д — эпюра изгибающих моментов от действия единичного момента; е — суммарная эпюра изгибающих моментов от действия силы P/2 и момента X₁; ж — эпюра изгибающих моментов от действия единичной силы» [1]

Учитывая, что в нашем случае подвесов не 2, а 4, тогда воздействующая сила P распределится на каждую балку поровну и составит P/4.

«Для определения момента в опорах воспользуемся методом Верещагина, заменив момент в опоре на единичный. Уравнение для перемещения в опоре, равного нулю при действии силы P/4 и M₁, запишется в виде» [1]:

                                                                     (3)

Перемещение от действия силы P/4, моментов M_P (момент от действия силы) и M_m (момент, возникающий в центре масс) определяется как:

                                                         (4)

где: J_x — осевой момент инерции поперечного сечения опоры при изгибе;

                                                 (5)

Подставив (5) в (4) получим:

                                                  (6)

В результате решения (6) получим перемещение равное:

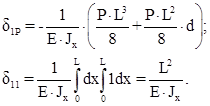                                                        (7)

Откуда реактивный момент равен:

                                                              (8)

Статическое перемещение δ центра тяжести инерционной массы определяется из уравнения:

                                                                   (9)

где:

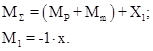                                                               (10)

Подставив (10) в (9) получим:

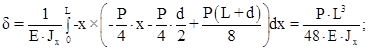                                   (11)

где:

                                               (12)

Подставив (12) в (11) получим:

                                                 (13)

Для начала расчета параметров конструкции гребенчатого ЧЭ необходимо задать некоторые параметры: длина «пальцев» гребенки — L_f = 435 мкм, число групп ёмкостей, образованное неподвижными гребёнками в одном ряду — N = 26, зазор между гребёнками — (d₁ = 2,5 мкм, d₂ = 12,5 мкм), толщину гребенки — t = 30 мкм. Используемые константы: диэлектрическая постоянная — ε₀ = 8,85∙10^- 12 Ф/м, модуль Юнга — Е = 1,7∙10¹¹ Па, коэффициент Пуассона — ρ = 2330 кг/м³).

Для достижения желаемой чувствительности будем варьировать некоторыми из перечисленных параметров, исходя из требований конструкторских и технологических возможностей. Для этого расчета будем использовать программу MatLab, фрагмент окна которой представлен на рисунке 4.

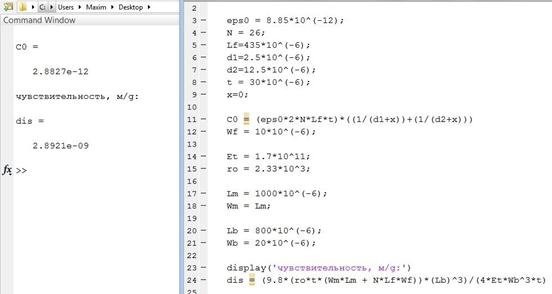
Рисунок 4. Расчет параметров в MatLab

В результате получим следующие конструктивные параметры ЧЭ: ёмкость в отсутствии ускорения — C₀ = 2,8 пФ, ширина «пальцев» гребенки — W_f = 10 мкм, ширина инерционной массы — W_f = 1000 мкм, длина инерционной массы — L_m = 1000 мкм, длина рамки — L_b = 800 мкм, ширина рамки — W_b = 20 мкм, чувствительность ЧЭ — dis → δ = 2,8921∙10^-9 м/g.

Далее проведем расчет перемещения инерционной массы под воздействием ускорения в программе ANSYS с целью более точного анализа, а также для проверки рассчитанных параметров, рисунок 5.

Рисунок 5. Результат моделирования ЧЭ в ANSYS

Из результата моделирования видно, что чувствительность ЧЭ составляет — δ = 2,8987∙10^-9 м.

Анализируя полученные значения чувствительности ЧЭ в результате теоретического расчета и моделирования в ANSIS видно, что разница лишь в тысячных долях, следовательно, это дает возможность сделать вывод о том, что все расчеты произведены верно.

Далее определим передаточную характеристику ЧЭ, представлено в таблице 1, на основе данных, полученных в результате моделирования ЧЭ в ANSIS, для этого будем задавать ускорения в диапазоне от 1 g до 100 g с шагом 10 g, таблица 1.

Таблица 1.

Расчетные значения перемещений инерционной массы в диапазоне 1—100 g

Далее проведем аппроксимацию полученных точек полиномом 1-й степени в MatLab, рисунок 6.

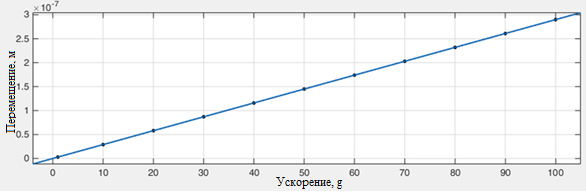
Рисунок 6. Результат аппроксимации в MatLab

В результате проведения аппроксимации в MatLab получены коэффициенты, рисунок 7.

Рисунок 7. Полученные коэффициенты в результате аппроксимации

Выпишем представленные коэффициенты на рисунке 7 для более удобного представления: масштабный коэффициент — р₁ = 2.899∙10^-9 м, смещение нуля — р₂ = 6.231∙10^-16 м.

Подставляем полученные коэффициенты в (2) получим выражение для нахождения емкости в зависимости от приложенного ускорения:

                           (14)

где: а, [м/с²] — ускорение, действующее на ЧЭ.

Полученное выражение (14), также можно использовать для создания spice моделей в различных САПР.

Список литературы:

1. Тимофеев В.Н. Техническая механика микросистем. Учеб. Пособие. — М.: МИЭТ, 2006. — 187 с.

2. Shalimov A., Timoshenkov S., Golovinskiy M., “Comb structure analysis of the capacitive sensitive element in MEMS — accelerometer”, Micro- and nanotechnology (MNT) sensors, systems, and applications 18 conference, Baltimore, MD, 20—24 April 2015.