РЕЗУЛЬТАТЫ РЕАЛИЗАЦИИ НЕЧЕТКОГО АЛГОРИТМА ОБРАБОТКИ ЗАЯВОК АБОНЕНТОВ ТЕЛЕКОММУНИКАЦИОННЫХ КОМПАНИЙ

Эффективность функционирования службы технической поддержки (СТП) интернет – провайдера оценивается при помощи определенного набора количественных показателей, важнейшим из которых, с точки зрения потребителя, является время решения инцидента. Началом этого временного отрезка является момент регистрации инцидента оператором первой линии и заканчивается подтверждением абонента о том, что его техническая проблема устранена. Очевидно, что решение инцидента, в отличие от его регистрации, может иметь место на любом уровне СТП. Поэтому очень важно, как можно раньше определить причину инцидента или, по крайней мере, его границу: проблема с оборудованием абонента или провайдера, проблема физического характера (повреждение линии) или логического (настройки оборудования) и т. д. Это является первоочередной задачей специалистов первого уровня СТП.

Для правильной классификации инцидента, которая определяет алгоритм его решения, воспользуемся аппаратом нечеткой логики. В статье [1] были построены наборы лингвистических переменных, предназначенных для реализации алгоритма определения границ инцидента для различных технологий предоставления доступа. Рассмотрим один из этих наборов, например, для xDSL технологии (в случае FTTx аналогично).

Входные переменные: a₁ – длительность активности порта, множество термов t₁ = {«большая», «средняя», «небольшая»}; a₂ – длительность авторизации, множество термов t₂ = {«большая», «средняя», «небольшая»}; a₃ – отношение скоростей соединения и тарифного плана, множество термов t₃ = {«соответствует», «ниже нормы», «не соответствует»}; a₄ – затухание, множество термов t₄ = {«критичное», «высокое», «среднее», «нормальное»}; a₅ – SNR (соотношение сигнал/шум), множество термов t₅ = {«отличное», «хорошее», «среднее», «низкое»}; a₆ – количество обрывов за сутки у абонента, множество термов t₆ = {«очень много», «много», «средне», «немного»}.

Выходные переменные: y₁ – качество линии, множество термов t¹ = {«отличное», «хорошее», «среднее», «плохое»}; y₂ – нестабильность услуги, множество термов t² = {«физическая», «нулевая», «логическая»}.

В статье [1] наглядно представлена структура всех перечисленных переменных, а также их числовые области определения. Необходимо уточнить, что переменная a₆ обозначает количество обрывов за сутки, зарегистрированных абонентом, что не говорит об их реальном наличии, так как в этом контексте они могут быть просто обусловлены аппаратными или программными сбоями оборудования абонента, или какими-нибудь другими причинами, не зависящими от провайдера.

Функции принадлежности для всех нечетких переменных заданы таблично на основе значений экспертных оценок и идентифицированы с помощью MS Excel на основе:

1.  S – образной функции принадлежности [2, с. 56], задаваемой в общем виде формулой:

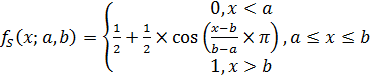                              (1)

2.  Z – образной функции принадлежности [2, с. 54], задаваемой в общем виде формулой:

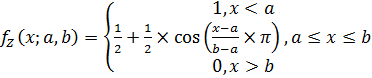                              (2)

3.  П – образной функции принадлежности [2, с. 61], задаваемой в общем виде формулой:

                                  (3).

Результаты идентификации функции принадлежности для каждого терма выходных переменных представлены в таблице 1.

Таблица 1.

Результаты идентификации функций принадлежности

Для использования идентифицированных функций принадлежности в программном комплексе MATLAB была построена система нечеткого вывода, основанная на алгоритме Мамдани. Данный алгоритм описывает несколько последовательно выполняющихся этапов, при этом каждый последующий этап получает на вход значения, полученные на предыдущем шаге. Алгоритм примечателен тем, что он работает по принципу черного ящика. На промежуточных этапах используется аппарат нечеткой логики и теория нечетких множеств.

Для реализации алгоритма Мамдани была разработана база правил:

1.  ЕСЛИ “SNR” есть «Отличное» И «Затухание» есть «Нормальное» ТО «Качество линии» = «Отличное»;

2.  ЕСЛИ “SNR” есть «Хорошее» И «Затухание» есть «Нормальное» ТО «Качество линии» = «Хорошее»;

3.  ЕСЛИ “SNR” есть «Среднее» И «Затухание» есть «Среднее» ТО «Качество линии» = «Среднее»;

4.  ЕСЛИ “SNR” есть «Низкое» И «Затухание» есть «Критичное» ТО «Качество линии» = «Низкое»;

5.  ЕСЛИ “SNR” есть «Низкое» И «Затухание» есть «Высокое» ТО «Качество линии» = «Низкое»;

6.  ЕСЛИ “SNR” есть «Среднее» И «Затухание» есть «Критичное» ТО «Качество линии» = «Низкое»;

7.  ЕСЛИ “SNR” есть «Хорошее» И «Затухание» есть «Критичное» ТО «Качество линии» = «Низкое»;

8.  ЕСЛИ «Длительность активности порта» есть «Большая» И «Длительность авторизации» есть «Большая» ТО «Нестабильность услуги» = «Нулевая»;

9.  ЕСЛИ «Длительность активности порта» есть «Большая» И «Длительность авторизации» есть НЕ «Большая» ТО «Нестабильность услуги» = «Логическая»;

10. ЕСЛИ «Длительность активности порта» есть НЕ «Большая» И «Длительность авторизации» есть «Большая» ТО «Нестабильность услуги» = «Физическая»;

11.  ЕСЛИ «Отношение скоростей» есть «Не соответствует» И «Количество обрывов» есть «Очень много» ТО «Нестабильность услуги» = «Физическая»;

12.  ЕСЛИ «Длительность активности порта» есть «Большая» И «Длительность авторизации» есть «Большая» И «Количество обрывов» есть «Очень много» ТО «Нестабильность услуги» = «Нулевая»;

13. ЕСЛИ «Отношение скоростей» есть «Соответствует» И «SNR» есть «Отличное» ТО «Нестабильность услуги» = «Нулевая»;

14.  ЕСЛИ «Длительность активности порта» есть «Большая» И «Количество обрывов» есть «Очень много» ТО «Нестабильность услуги» = «Логическая».

В качестве экспериментальной базы для проверки предложенного алгоритма использовали исходные данные некоторых инцидентов одного из провайдеров Оренбургской области.

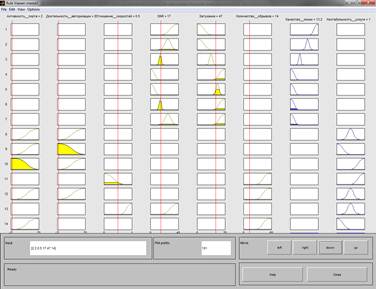
Рисунок 1. Результат работы алгоритма Мамдани в MATLAB

Далее для каждого инцидента был реализован алгоритм Мамдани для получения численных значений выходных параметров, на основании которых должно приниматься первоначальное решение о направлении решения инцидента. Дефаззификация выходных лингвистических переменных проводилась методом центра тяжести. На рисунке 1 представлен результат работы алгоритма Мамдани для инцидента № 8 из таблицы № 2.

В таблице 2 представлены результаты экспертной оценки параметров для каждого инцидента, являющихся входными лингвистическими переменными и рассчитанные на их основе с помощью программной среды MATLAB значения выходных лингвистических переменных.

Таблица 2.

Оценки входных и выходных лингвистических переменных

Инструментальные средства MATLAB позволяют также просмотреть с целью анализа поверхности нечеткого вывода, где необходимо выбрать одну выходную и две входные переменные [2]. Это дает наглядно увидеть зависимость выходных переменных от входных. Например, на рисунке 2 видна сильная зависимость переменной «Качество линии» от входных переменных “SNR” и «Затухание».

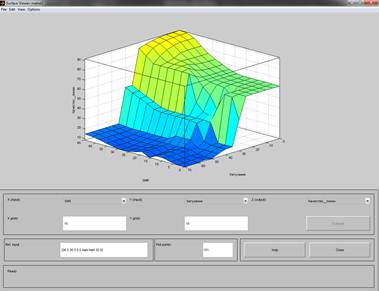
Рисунок 2. Зависимость выходной переменной «Качество линии» от входных переменных “SNR” и «Затухание»

А на рисунке 3 видна сильная зависимость выходной переменной «Нестабильность услуги» от входных – «Длительность активности порта» и «Длительность авторизации».

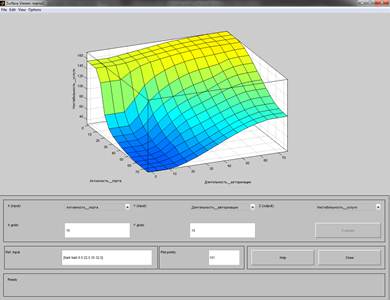
Рисунок 3. Зависимость выходной переменной «Нестабильность услуги» от входных переменных «Длительность активности порта» и «Длительность авторизации»

Предложенная система нечеткого вывода позволяет уже на первом уровне СТП, то есть при регистрации инцидента, продиагностировать инцидент и определить границы инцидента, таким образом, уже начать его решение. Если, например, выходная переменная «Качество линии» принимает значения, свидетельствующие о низком качестве линии, то инцидент есть смысл передать сразу на выездную бригаду для устранений повреждений на линии, минуя второй уровень СТП, как избыточный в данной ситуации. В среднем это позволит снизить время решения инцидента. А дальнейшее добавление входных и выходных переменных, развитие базы знаний, позволит еще точнее проводить первоначальную диагностику.

Список литературы:

1. Гаибова Т.В. Управление инцидентами технического обслуживания абонентов телекоммуникационных компаний на основе нечеткой логики [Текст] / Т.В. Гаибова, Л.Ю. Кубарева // Молодой ученый. – 2015. – № 19. – С. 121–125.
2. Леоненков А. Нечеткое моделирование в среде MATLAB и fuzzyTECH. СПб: БХВ – Петербург, 2005. – 736 с.