ТРАЕКТОРИИ ОБУЧЕНИЯ ПРОСТЕЙШЕГО ЛИНЕЙНОГО ПЕРСЕПТРОНА

В данной работе численными методами исследованы траектории обучения простейшего двуслойного линейного персептрона , где – входной вектор, ,  – линейные операторы. Обучением на заданных входных векторах  и соответствующих выходных векторах  называется градиентный спуск в пространстве операторов  и  с целевой функцией 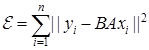. В этом случае траектории операторов, рассматриваемых как матрицы,  и  задается автономной системой обыкновенных дифференциальных уравнений

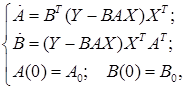                                                                             (1)

где:

и матрицы, составленные из столбцов  и  соответственно, , –начальное состояние, выбираются случайные матрицы. В работе [2] были построены точные решения системы (1) в случае одновременно диагонализируемых (t) и (t). В этом случае задача распадается на несколько простейших задач на плоскости. В этих задачах на плоскости (t) и (t) являются функциями. Для иллюстрации траекторий обучения на плоскости в работе [2] было предложено рассматривать в качестве траекторий обучения персептрона кривые на . Опишем эти кривые. Во-первых, система (1) имеет первый интеграл (т.е. не меняющуюся со временем величину) [1]:. Это означает, что каждая траектория лежит на гиперболе , где постоянные  являются начальными данными A(0) и B(0). Во-вторых, множество решений уравнения  имеет вид .

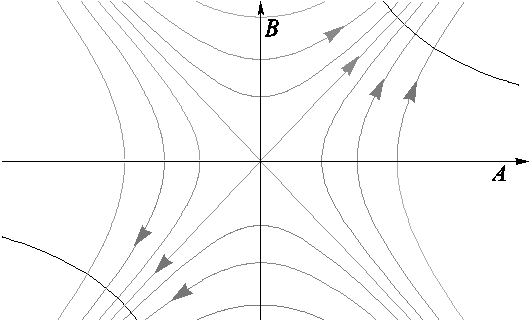
Рисунок 1. Траектории обучения ,

Таким образом, траектории обучения одномерного персептрона лежат на ветви гиперболы вида

и монотонно стремятся в точку пересечения с гиперболой вида .

В данной работе мы рассматриваем простейший случай, когда

, ,, . В этом случае система (1) также имеет первый интеграл , который определяет гиперболоид или конус. Заметим, что этот гиперболоид (или конус) полностью определяется начальными данными  системы (1). Тип поверхности первого интеграла – однополостный гиперболоид, двуполостный гиперболоид или конус –зависит от числа const. Во-вторых, все решения системы (1) имеют вид 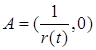, , т.е. лежат на кривой (гиперболе) в пространстве. Ветви гиперболы решений пересекают гиперболоид первого интеграла в двух точках, которые являются точками притяжения траекторий решения. Наши численные эксперименты показывают, что для малых по модулю начальных данных p0, q0 и r0 типичная картина траекторий обучения приведена на рис. 2.

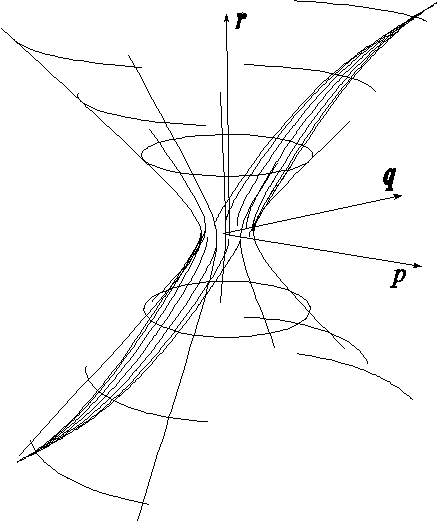
Рисунок 2. Траектории обучения

На рисунке 2 построены траектории с начальными данными на экваторе однополосного гиперболоида. Траектории разбились на две группы. Каждая группа траекторий сошлась к своей точке притяжения. В силу симметрии задачи и выбранных начальных данных рисунок получился симметричным.

Заключение

1.  В работе [2] был рассмотрен случай одновременно диагонализируемых

 и . В этом случае анализ градиентного спуска сводится к анализу траекторий на плоскости, что было показано в [2]. В данной работе с помощью численных методов рассмотрены траектории обучения в случаях, которые не были охвачены работой[2].

2.  В результате численных экспериментов для малых по модулю значений начальных данных p0, q0и r0 мы увидели, что траектории обучения

 и  ведут себя как в диагонализируемом случае.

3.  В ходе численных экспериментов не удается построить иллюстрирующие примеры эффектов переобучения и замедления обучения из-за локальных минимумов.

Список литературы:

1.Guo H., GelfandS.B.Analysis of gradient descent learning algorithms for multilayer feed forward neural networks // IEEE Transactions on Circuits and Systems. –1991. –Vol. 38.–№ 8.–P.883–894.

2.Saxe A.M., McClelland J.L., Ganguli S. Exact solutions to the nonlinear dynamics of learning in deep linear neural networks [Электронный ресурс].URL: http://arxiv.org/abs/1312.6120 (дата обращения 10.01.2016).