ОБОСНОВАНИЕ КИНЕТИЧЕСКОГО УРАВНЕНИЯ РАСПАДА ПЕРЕОХЛАЖДЕННОГО АУСТЕНИТА В БЕЙНИТНОЙ ОБЛАСТИ ХРОМОНИКЕЛЬМОЛИБДЕНОВЫХ СТАЛЕЙ

Работа выполнена при финансовой поддержке гранта Президента Российской Федерации для государственной поддержки молодых ученых МК- 7929.2016.8

Существует достаточно большое число уравнений для аналитического описания превращений переохлажденного аустенита в сталях, В основе большинства методик лежат классическая теория зарождения и роста [6,7] и уравнение Колмогорова-Джонсона-Мела-Аврами (КДМА) [3–5], позволяющие оценить кинетику формирования новых фаз и структурных составляющих, как при изотермической выдержке, так и при непрерывном охлаждении

P=1-exp(-kτⁿ),                                            (1)

где: Р – доля превращенного аустенита, τ – время, k – температурно-зависимый коэффициент, n – показатель степени. При этом подразумевается, что коэффициент n должен иметь постоянное значение (определяемое типом превращения, химическим составом стали и т.д.) на протяжении всего процесса изотермического превращения. В ряде работ утверждается конкретное значение, которое должен принимать коэффициент n для исследуемого процесса [14,,15,10]. Однако на практике, при анализе экспериментальной кинетики изотермического превращения переохлажденного аустенита наблюдаются весьма существенные отклонения от общепринятой теории [11,5.8]:

·      коэффициент n может принимать любое положительное действительное значение, зависящее не только от типа превращения, но также от температуры и других факторов, достигая в ряде случаев величин, существенно превышающих допускаемый теорией интервал;

·      коэффициенты k и n зависят не только от температуры изотермического превращения, но также немонотонно изменяются во времени, в течение которого протекает превращение.

В случае соблюдения всех условий теории расчетные результаты весьма неудовлетворительно описывают экспериментальные данные [12,9].

Решение проблемы состоит в отыскании функции, которая обеспечила бы максимально точное математическое описание наблюдаемых явлений при минимальном количестве параметров оптимизации.

Исходными данными для расчета кинетики образования бейнита в изотермических условиях являлись экспериментальные изотермические диаграммы распада переохлажденного аустенита сталей 34ХН3М, 12ХН4М, 20Х2Н2М, 30ХН3М [2]. Для описания изотермической кинетики бейнитного превращения использовалось уравнение КДМА.

Проведена оцифровка изотермических диаграмм распада переохлажденного аустенита доэвтектоидных конструкционных сталей, опубликованных в [2] с помощью программы «GetData Graph Digitizer 2.26», определено время для линий условного начала, 10%, 50%, 90%, 95% бейнитного превращения

На рисунках 1-3 приведены графики зависимости двойного логарифма доли бейнитного превращения ln(-ln(1-P)), кинетических коэффициентов n и ln k от логарифма времени для стали 30ХН3М.

Рисунок 1. Зависимость двойного логарифма доли бейнитного превращения ln(-ln(1-P)) от логарифма времени ln τ; сталь 30ХН3М, температура изотермической выдержки 340 °С

С течением времени изотермической выдержки при температуре 340º°С параметр n изменяется от 0,2 до 2,8 (рисунок 2). Аналогичным образом ведет себя временная зависимость логарифма коэффициента k (ln k) (рисунок 3).

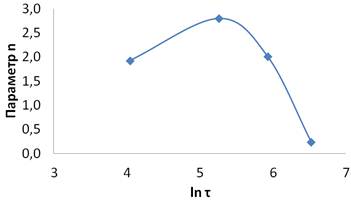
Рисунок 2 Зависимость параметра n от логарифма времени ln τ; сталь 30ХН3М, температура изотермической выдержки 340°С

Рисунок 3 Зависимость ln k от логарифма времени ln τ; сталь 30ХН3М, температура изотермической выдержки 340°С

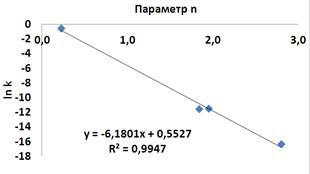
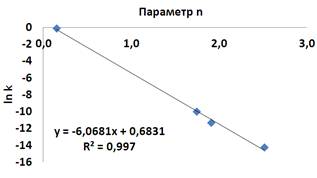
На рисунке 4 представлены зависимости величины ln k от параметра n бейнитного распада аустенита стали 30ХН3М для температур изотермических выдержек 320°С, 360 °С, 380 °С, 390 °С. Наблюдаемые зависимости строго линейные, коэффициент детерминации r² составляет 0.995…0,997.

а)

б)

в)

г)

Рисунок 4 Зависимость ln k от параметра n; сталь 30ХН3М

Кинетический параметр n численно равен первой производной двойного логарифма доли превращения по логарифму времени, а величина ln k является свободным членом уравнения касательной к графику зависимости ln(-ln(1-P)) от ln τ. Следовательно, используя известное уравнение касательной к кривой [3], и учитывая линейную зависимость ln k от параметра n вида:

ln k=a*n+b                                                  (2)

можно записать следующее дифференциальное уравнение

y(x) – y’(x) = ay’(x)+b                               (3)

где x= ln τ, y(x) = ln(-ln(1-p))                              (4)

Решением данного дифференциального уравнения является уравнение вида:

y(x) = C₁exp(C₂x)+C₃                                           (5)

Учитывая уравнения (4) приходим к уравнению:

ln(-ln(1-p))=C₁exp(C₂lnτ)+C₃,                              (6)

и в конечном итоге зависимость кинетики бейнитного превращения от времени изотермической выдержки выразится уравнением

P = 1-exp(-(exp(C₁τ^C2)expC₃)                                        (7)

где: С₁, С₂, С₃ являются константами для каждой температуры изотермической выдержки и в обобщенном виде функциями температуры для интервала бейнитного превращения. Поскольку время и доля превращения взяты из справочных данных [2] с заранее неизвестной погрешностью, то для устойчивого определения температурно-зависимых коэффициентов С₁, С₂, С₃ применили функцию «Поиск решения» в MS Excel.

Для расчета времени образования фиксированных долей бейнитного превращения использовано уравнение

τ = (((ln(-ln(1-P))-C₃)/C₁)^(1/C₂)                                    (8)

На рисунке 5 приведены фрагменты расчетной и экспериментальной изотермических диаграмм бейнитного превращения стали 30ХН3М для различной степени превращения. Наблюдается удовлетворительное совпадение расчетных и экспериментальных точек для всех температурно-временных интервалов.

Рисунок 5 Расчетная (линии) и экспериментальная (точки) [14, диаграмма 426] изотермические диаграммы распада переохлажденного аустенита стали 30ХН3М в бейнитной области

Список литературы:

1. Колмогоров А.Н. К статистической теории кристаллизации металлов / А.Н. Колмогоров. Известия АН СССР, 1937. № 3. С. 355−359.

2. Попова Л.Е., Попов А.А. Диаграммы превращения аустенита в сталях и β- раствора в сплавах титана: справочник термиста. // М.: Металлургия. 1991. 503 с.

3. Пискунов Н.С. Дифференциальное и интегральное исчисления. //Учеб., т.1, СПб, МИФРИЛ, 1996. 416 с.

4. Avrami M. Kinetics of phase change I. General theory // J. Chem. Phys. Vol. 7. 1939. PP. 1103−1112.

5. Boyadjiev I.I., Thomson P.F., Lam Y.C. Computation of the Diffusional Transformation of Continuously Cooled Austenite for Predicting the Coefficient of Thermal Expansion in the Numerical Analysis of Thermal Stress // ISIJ International. Vol. 36. 1996. № 11. P. 1413-1419.

6. Cahn R.W., Haasen P. Physical Metallurgy. Vol. 2. Amsterdam: North-Holland, 1996. 940 p.

7. Christian J.W. The Theory of Transformations in Metals and Alloys. Amsterdam: Pergamon, 2002. 1200 p.

8. Fang L., Wood W. E., D. G. Atteridge. Identification and range quantification of steel transformation products by transformation kinetics // Metallurgical and Materials Transactions A. Vol. 28. №1. 1997. P. 3–14.

9. Gómez M., Medina S. F., Caruana G. Modelling of Phase Transformation Kinetics by Correction of Dilatometry Results for a Ferritic Nb-microalloyed Steel // ISIJ International. Vol. 43. №8. 2003. P. 1228–1237.

10. Han H. N., Lee J. K. A Model for Carbon Steal Phase Transformation and Cooling Behavior on Run-Out Table of Hot Strip Mill // Metals And Materials. Vol 6. № 5. 2000. P. 401-406.

11. Heming C., Shuhong Z., Honggang W., Jianyun L. Finite Element Analysis Of Temperature Field With Phase Transformation And Non-Linear Surface Heat-Transfer Coefficient During Quenching // Applied Mathematics and Mechanics. Vol. 19. №1. 1998. P. 15-20.

12. Jia T., Militzer M., Liu Z. Y. General Method of Phase Transformation Modeling in Advanced High Strength Steels // ISIJ International. Vol. 50. №4. 2010. P. 583–590.

13. Johnson W.A., Mehl R.F. Reaction kinetics in processes of nucleation and growth // Trans. AIME. Vol. 135. 1939. PP. 416−468.

14. Nagasaka Y., Brimacombe J.K., Hawbolt E.B., Samarasekera I.V., Hernandez-Morales B., Chidiac S.E. Mathematical Model of Phase Transformations and Elasto-Plastic Stress in the Water Spray Quenching of Steel Bars // Metallurgical Transactions A. Vol. 24. 1993. P. 795-808.

15. Zou J., Tseng A.A. Microscopic Modeling of Fundamental Phase Transformations in Continuous Castings of Steel // Metallurgical Transactions A. Vol. 23. 1992. P. 457-467.