ПРОВЕРКА АДЕКВАТНОСТИ МОДЕЛИ АНОДНЫХ ПРОЦЕССОВ НА ИНЕРТНЫХ АНОДАХ В КРИОЛИТ-ГЛИНОЗЕМНЫХ РАСПЛАВАХ
Секция: 3. Информационные технологии

XXXIII Студенческая международная заочная научно-практическая конференция «Молодежный научный форум: технические и математические науки»
ПРОВЕРКА АДЕКВАТНОСТИ МОДЕЛИ АНОДНЫХ ПРОЦЕССОВ НА ИНЕРТНЫХ АНОДАХ В КРИОЛИТ-ГЛИНОЗЕМНЫХ РАСПЛАВАХ
Введение
В современном мире в производстве алюминия в основном используется технология, основанная на электролизе криолит-глиноземного расплава при температуре 960°С с помощью углеродных анодов. Такая технология является материало-, энергоемкой и экологически опасной [5-8]. Для решения этих проблем существует два пути: снижение температуры процесса и использование инертных анодов, таких, как кислородвыделяющие аноды.
В настоящее время широко исследуется возможность внедрения новой технологии, основанной на электролизе расплава KF–NaF–AlF3–Al2O3 в температурном диапазоне 750–850°С на кислородвыделяющих анодах [9]. По этой причине изучение электрохимических свойств кислородвыделяющих анодов в данном расплаве в указанном температурном интервале является важной частью развития новой технологии производства алюминия.
В ряде работ [2] была исследована кинетика анодных процессов на угольных анодах в расплаве KF–NaF–AlF3–Al2O3 в температурном диапазоне 750–850°С. Результаты этого исследования показали, что анодный процесс состоит из двух стадий: на первой стадии идет поверхностное взаимодействие угольного анода с кислородной частицей в расплаве с последующим выделением угарного газа на второй стадии. Далее эти исследования были продолжены для других анодных материалов, а именно кислородвыделяющих анодов [1,3,4].
Таким образом, целью данной работы является моделирование кинетики анодных процессов на кислородвыделяющих анодах в криолит-глиноземных расплавах на примере механизма анодного процесса на платиновом аноде в расплаве KF–NaF–AlF3–Al2O3 при температуре 750–850°С.
Теоретические основы модели
Предполагается [3], что механизм анодного процесса на платиновом аноде в расплаве KF–NaF–AlF3–Al2O3 состоит из двух основных этапов: образование промежуточного оксидного соединения на поверхности платины (1) и дальнейший распад этого соединения по электрохимическому механизму (2) (с переносом электрона), либо химическому (3) (без переноса электрона).
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
Равновесие электроактивных частиц (Al2O2F42- и Al2OF62-) задается следующим уравнением [1]:
![]()
Плотность парциального тока для данных процессов может быть записана следующим образом:
![]() (4)
(4)
![]() (5)
(5)
 (6)
(6)
где: i01, i02, i03 – токи обмена соответствующих реакций; θ, θ0 – степень заполнения поверхности анода соединением PtxOabs при i > 0 и i = 0 соответственно; x, y, z (x0, y0, z0) – концентрации (моль*см-1) соединений Al2O2F42-, Al2OF62- и кислорода вблизи к поверхности анода (диффузионный слой) при i > 0 и i = 0 соответственно.
Фарадеевский ток процесса равен сумме первого и второго токов обмена:
![]() (7)
(7)
Переходя к кинетическим процессам, нужно установить зависимости неизвестных в модели (потенциал, концентрации и степень заполнения поверхности промежуточными соединениями) от времени.
Зависимость потенциала от времени определяется разницей между подаваемым током и фарадеевским током:
![]() (8)
(8)
где: Cd – емкость двойного электрического слоя.
В первую стадию анодного процесса (1) поверхность платинового анода заполняется, и освобождается во вторую стадию (2), (3). Таким образом, плотность парциального тока при этих процессах влияет на степень заполнения поверхности анода (9).
![]() (9)
(9)
где: N0 – количество вещества в монослое (4*10-9).
Концентрации веществ X и Y в диффузионном слое зависят и от диффузии, и от химических взаимодействий между ними, в то время как изменение по времени концентрации кислорода зависит только от диффузии.
![]() (10)
(10)
![]()
![]()
где: Dx, Dy, Dz – коэффициенты диффузии веществ x, y и кислорода (z); k – динамическая константа реакции (1), характеризующая изменение соотношения форм частиц k=x/y2 в ходе процесса; k1-k4 – прямые и обратные константы скорости реакций (1-2), определенные в уравнениях (10-11).
Граничные условия для уравнений x и y на левой границе зависят от фарадеевского тока:
![]() (13)
(13)
![]() (14)
(14)
Поскольку кислород выделяется на второй стадии, условия для левой границы в уравнении для концентрации кислорода зависит от суммы парциальных токов этих реакций (2-3):
![]() (15)
(15)
Одной из задач данной работы является создание программного обеспечения для расчета модели анодного процесса на платиновом аноде в расплаве KF–NaF–AlF3–Al2O3 при температуре 750–850°С для проверки ее адекватности. Адекватность модели проверялась путем сопоставления расчетных результатов с экспериментальными данными, полученными в ходе исследования стационарных анодных процессов на платиновом аноде в расплаве KF–NaF–AlF3–Al2O3 при температуре 750–850°С [3].
Методика расчета
Согласно методу интегрирования, для уравнений (8-9) значение искомой функции можно рассматривать как сумму ее значения в предыдущей точке и ее приращения на текущем отрезке аргумента. В таком случае, уравнения (8-9) в общем виде будут выглядеть следующим образом:
![]()
![]() (16)
(16)
В частности, на первом слое, когда Nui-1 отсутствует, а также парциальные токи равны нулю, уравнение (16) принимает следующий вид:
![]()
а начальная степень заполнения поверхности θ1 задана и равна 0.1.
Поскольку первый слой соответствует состоянию системы в первый момент включения тока, когда анодный процесс еще не начался, концентрации веществ одинаковы на любом расстоянии от анода и равны начальным концентрациям. Их значения в любой точке определяются по следующим формулам:


где: Z – концентрация Al2O3, которая равна 0.000304. Концентрация кислорода z0 задана изначально и равна 0.0000001.
Поскольку концентрации и степень заполнения поверхности в первый момент времени равны начальным значениям, то соответствующие коэффициенты перед экспонентами в уравнениях (4-5) обратятся в единицу, и уравнения примут вид:
![]() (17)
(17)
![]() (18)
(18)
а парциальный ток для процесса (3) будет равен 0.
Для расчета плотности парциального тока на остальных слоях используются уравнения (4-6).
Для нахождения концентраций x, y и z были составлены следующие уравнения по явной схеме:
![]() (19)
(19)
![]() (20)
(20)
![]() (21)
(21)
Хотя явная схема довольно проста в использовании, она является неустойчивой для данной модели. По этой причине уравнения (19-21) были адаптированы для неявной разностной схемы, шаблон которой представлен на рисунке 1.

Рисунок 1. Шаблон неявной разностной схемы
Неявная разностная схема содержит в каждом уравнении сразу несколько неизвестных значений нового слоя. Для каждого временного слоя неявная схема сводится к системе линейных уравнений, позволяющих определить искомые значения на слое k+1. Матрица такой системы уравнений является трехдиагональной, поэтому ее решение можно найти с помощью метода прогонки. В общем виде такая матрица имеет следующий вид:
 (22)
(22)
В соответствии с представленным на рисунке 1 шаблоном, уравнения (10-12) приняли вид:
 (23)
(23)
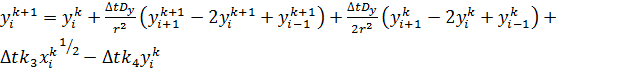 (24)
(24)
![]() (25)
(25)
Чтобы вычислить значения концентраций методом прогонки, на основании системы уравнений (22) с учетом граничных условий (13-15) составлены три системы уравнений для x (26), y (27) и z (28):
|
|
(26) |
|
|
(27) |
|
|
(28) |
Согласно методу прогонки, неизвестные вычисляются обратной прогонкой по формулам (29-30).
![]() (29)
(29)
![]() (30)
(30)
где: U – неизвестная величина на данном расчетном слое.
Коэффициенты C и D для (29-30) вычисляются прямой прогонкой по формулам (31-32).
![]() (31)
(31)
![]() (32)
(32)
Поскольку концентрации x1, y1 и z1 находятся из граничных условий (13-15) без метода прогонки, начальными коэффициентами будут C2 и D2:
![]() (33)
(33)
![]() (34)
(34)
Концентрация x для слоя k+1 вычисляется по формулам (29-34) с помощью коэффициентов b, α, β и γ, полученных из системы уравнений (26):
![]()
![]()
![]()
![]()
![]()
![]()
yk+1 вычисляется аналогично с помощью коэффициентов, полученных из системы уравнений (27):
![]()
![]()
![]()
![]()
![]()
![]()
Для zk+1 коэффициенты получены из системы уравнений (28):
![]()
![]()
![]()
![]()
![]()
![]()
Результаты и обсуждения
Данные, полученные в результате расчетов, были сравнены с экспериментальными данными. Результат сравнения приведен на рисунке 2.

Рисунок 2. Сопоставление расчетных и экспериментальных данных
Как видно на рисунке 2, расчетная и экспериментальная кривые симбатны при следующих условиях:
· Коэффициенты диффузии веществ X и Y одинаковы и равны 0,00001; коэффициент диффузии кислорода – 0,0001 (значения подобраны вручную);
· Токи обмена i01=0,44 А/см2, i02=0,04 А/см2, i03=0,02 А/см2 [2];
· Температура задана изначально и равна 1053K.
Таким образом, результаты расчетов показывают, что принятая математическая модель адекватна реальным процессам, протекающим в системе платиновый анод – криолит-глиноземный расплав.
Вывод
В ходе работы была рассчитана математическая модель анодного процесса на платиновом аноде в расплаве KF–NaF–AlF3–Al2O3. В результате расчета был получен ряд данных (потенциал, степень заполнения поверхности анода, концентрации соединений Al2O2F42-, Al2OF62- и кислорода и парциальные токи реакций (1-3)). Потенциал и степень заполнения поверхности анода были рассчитаны методом интегрирования. Концентрации соединений Al2O2F42-, Al2OF62- и кислорода были адаптированы для неявной разностной схемы и рассчитаны методом прогонки. Плотность парциальных токов была рассчитана напрямую по формулам математической модели.
Расчетные и экспериментальные значения потенциалов дали хорошее совпадение, что подтверждает адекватность модели. Таким образом, модель может быть использована для дальнейшего изучения свойств кислородвыделяющих анодов. Ее применение позволит получить больше данных об анодном процессе (плотность парциального тока третьего процесса (3), потенциал, степень заполнения поверхности анода, а также концентрации соединений Al2O2F42-, Al2OF62- и кислорода в диффузионном слое) и сделать выводы об устойчивости исследуемых материалов анодов.
Список литературы:
1. Некрасов В.Н. Стационарный анодный процесс на платине в расплавах KF-NaF-AlF3-Al2O3 / Некрасов В.Н., Лимановская О.В., Суздальцев А.В., Храмов А.П., Зайков Ю.П. // Расплавы. – 2014. №4. – С. 71–79.
2. Некрасов В.Н. Хронопотенциометрия на углеродном аноде в расплавах KF–AlF3–Al2O3 / Некрасов В.Н., Лимановская О.В., Суздальцев А.В., Храмов А.П., Зайков Ю.П. // Расплавы. – 2011. №2. – С. 18–29.
3. Некрасов В.Н. Stationary anode process at the platinum in KF-NaF-AlF3-Al2O3 melts / Некрасов В.Н., Лимановская О.В., Суздальцев А.В., Храмов А.П., Зайков Ю.П. // Russian Metallurgy. – 2014. Vol. 8. – P. 664–670.
4. Суздальцев А.В. Хроновольтамперометрия на платине в расплаве KF–NaF–AlF3–Al2O3 / Суздальцев А.В., Храмов А.П., Лимановская О.В., Некрасов В.Н., Зайков Ю.П. // Расплавы. – 2015. №5. – С. 12–21.
5. Goupil G. Anodic behavior of mechanically alloyed Cu–Ni–Fe and Cu–Ni–Fe–O electrodes for aluminum electrolysis in low-temperature KF-AlF3electrolyte / Goupil G., Helle S., Davis B., Guay D., Roue L. // Electrochimica Acta. – Vol. 112. 2013. – P. 176–182.
6. Helle S. Structure and high-temperature oxidation behaviour of Cu–Ni–Fe alloys prepared by high-energy ball milling for application as inert anodes in aluminium electrolysis / Helle S., Pedron M., Assouli B., Davis B., Guay D., Roue L. // Corrosion Science. – Vol. 52. 2010. – P. 3348–3355.
7. Khramov A.P. Anodic behaviour of the Cu82Al8Ni5Fe5 alloy in low-temperature aluminium electrolysis / Khramov A.P., Kovrov V.A., Zaikov Yu.P., Chumarev V.M. // Corrosion Science. – Vol. 70. 2013. – P. 194–202.
8. Yang J. New opportunities for aluminum electrolysis with metal anodes in a low temperature electrolyte system / Yang J., Hryn J.N., Davis B.R., Roy A., Krumdick G.K., Pomykala Jr. J.A. // Light Metals. 2004. P. 321–326.
9. Zaikov Y., Khramov A., Kovrov V. et al. Electrolysis of aluminum in the low melting electrolytes based on potassium cryolite // Light Metals. – 2008. – P. 505–508.








