ТЕОРИЯ СПИСКОВ И ЕЕ ПРИМЕНЕНИЕ В РЕШЕНИИ ЗАДАЧ ТЕОРИИ МНОЖЕСТВ
Секция: 6. Математические науки
лауреатов
участников
лауреатов


участников



XXXIV Студенческая международная заочная научно-практическая конференция «Молодежный научный форум: технические и математические науки»
ТЕОРИЯ СПИСКОВ И ЕЕ ПРИМЕНЕНИЕ В РЕШЕНИИ ЗАДАЧ ТЕОРИИ МНОЖЕСТВ
Введение.
В работе описывается теория списков, которая позволяет решать некоторые задачи теории множеств. Данная теория была использована на интуитивном уровне в [1, c. 15] при решении ряда задач. В данной работе представлен переход от интуитивных размышлений к теории, основанной на теории множеств. Также рассмотрен пример решения системы уравнений относительно заданного множества, как вариант применения данной теории.
Определение α-элементов.
Пусть множества S1,..,Sn находятся в общем положении. Рассмотрим множество индексов ![]() а также множества индексов
а также множества индексов ![]() Каждое из множеств
Каждое из множеств ![]() представляет собой сочетание из n элементов, взятых по m штук.
представляет собой сочетание из n элементов, взятых по m штук.
Определение 1. Введем множества, определяемые следующим выражением:

Множества αk будем называть α-элементами.
Используя свойства ![]() и
и ![]() ,
,
получим
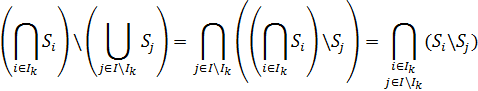
В результате имеем выражение для α-элементов, аналогичное (1):
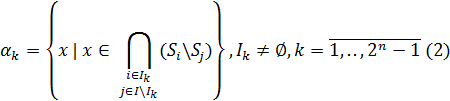
Таким образом каждому α-элементу мы поставили в соответствие набор элементов x из множества ![]()
Замечание. При наличии в задаче универсального множества U определим нулевой α-элемент следующим образом:
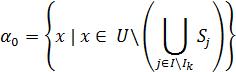
Свойства α-элементов.
Для α-элементов определим следующий набор свойств:
![]()

Докажем данные свойства.
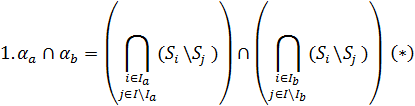
Из определения α-элементов можно сделать вывод о том, что верно либо выражение ![]() либо выражение
либо выражение ![]() либо оба этих выражения сразу. Тогда после раскрытия скобок в выражении (*) получим выражение, которое будет содержать конструкцию вида
либо оба этих выражения сразу. Тогда после раскрытия скобок в выражении (*) получим выражение, которое будет содержать конструкцию вида ![]() Так как
Так как ![]() то и
то и ![]()

В силу дистрибутивности операции объединения относительно операции пересечения можем записать, что ![]() Каждое множество
Каждое множество![]() в данном случае представляет собой объединение множеств вида
в данном случае представляет собой объединение множеств вида ![]() , взятых по одному из каждого пересечения
, взятых по одному из каждого пересечения ![]() То есть, например,
То есть, например, 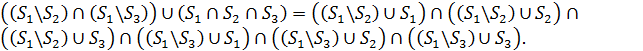 Тогда в разложении выражения
Тогда в разложении выражения ![]() встретится
встретится  Данное множество является минимальным из всех множеств
Данное множество является минимальным из всех множеств ![]() и равняется
и равняется ![]() Таким образом
Таким образом ![]()
Определение списков.
Определение 2. Каждому множеству ![]() поставим в соответствие множество α-элементов
поставим в соответствие множество α-элементов ![]() представимое в виде
представимое в виде

![]()
Данное множество будем называть списком.
По определению, множество![]() можно представить в виде
можно представить в виде
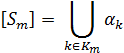
Но ранее было доказано, что ![]() Таким образом, список
Таким образом, список ![]() является аналогом разбиения множества
является аналогом разбиения множества ![]() за тем исключением, что подмножества(α-элементы) могут оказаться пустыми в процессе решения задачи.
за тем исключением, что подмножества(α-элементы) могут оказаться пустыми в процессе решения задачи.
Определим условия пустоты α-элементов:
![]()
![]()
Операции над списками.
Таким образом, поставив каждому множеству ![]() из набора множеств
из набора множеств ![]() список
список ![]() , мы можем свести операции над множествами к операциям над списками. Определим данные операции:
, мы можем свести операции над множествами к операциям над списками. Определим данные операции:
![]() - пересечение списков.
- пересечение списков.
![]() - объединение списков.
- объединение списков.
![]() - разность списков.
- разность списков.
![]() - симметрическая разность списков.
- симметрическая разность списков.
![]() - дополнение списка.
- дополнение списка.
Пример. Рассмотрим пример решения системы уравнений относительно множества Х с помощью списков.
Решить систему уравнений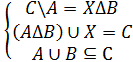
Будем полагать, что A = S1 , B = S2 , C = S3 , X = S4.
Множества индексов:
I1 = {1}, I2 = {2}, I3 = {3}, I4 = {4}, I5 = {1, 2}, I6 = {1, 3}, I7 = {1, 4}, I8 = {2, 3},
I9 = {2, 4}, I10 = {3, 4}, I11 = {2, 3, 4}, I12 = {1, 3, 4}, I13 = {1, 2, 4}, I14 = {1, 2, 3},
I15 = {1, 2, 3, 4}
α-элементы:
α0 = U\(A∪B∪C∪X), α1 = A\(B∪C∪X), α2 = B\(A∪C∪X), α3 = C\(A∪B∪X),
α4 = X\(A∪B∪C), α5 = (A∩B)\(C∪X), α6 = (A∩C)\(B∪X), α7 = (A∩X)\(B∪C),
α8 = (B∩C)\(A∪X), α9 = (B∩X)\(C∪A), α10 = (C∩X)\(B∪A), α11 = (B∩C∩X)\A,
α12 = (A∩C∩X)\B, α13 = (A∩B∩X)\C, α14 = (A∩B∩C)\X, α15 = A∩B∩C∩X
Составим списки для множеств:
[A] = {α1 , α5 , α6 , α7 , α12 , α13 , α14 , α15}.
[B] = {α2 , α5 , α8 , α9 , α11 , α13 , α14 , α15}
[C] = {α3 , α6 , α8 , α10 , α11 , α12 , α14 , α15}
[X] = {α4 , α7 , α9 , α10 , α11 , α12 , α13 , α15}
![]() .
.
![]() и
и![]() Тогда
Тогда ![]()
![]() ,
,
![]()
![]() Тогда
Тогда ![]()
![]() Т.к
Т.к ![]() и
и ![]() то пустых α-элементов не осталось.
то пустых α-элементов не осталось.
Итого ![]() Тогда
Тогда ![]()
Заключение.
В данной работе были введены понятия α-элементов, списков и основных операций над списками. Рассмотрен пример решения задачи из теории множеств, опирающийся на данные понятия и использующий введенные операции.

