ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ АЛГОРИТМА АСИНХРОННОГО ШИФРОВАНИЯ ЭЛЬ-ГАМАЛЯ И ЕГО РЕАЛИЗАЦИЯ ДЛЯ ОБМЕНА СООБЩЕНИЯМИ

Aннoтaция. Цeлью paбoты являeтcя создание системы для обеспечения безопасной передачи текстовых сообщений по незащищенным каналам связи. За основу был взят алгоритм работы асимметричного шифрования, предложенный Эль-Гамалем. Было выяснено, что разработанная система является эффективным средством для надежной передачи информации.

Ключевые слова: модульная арифметика, дискретное логарифмирование, асимметричное шифрование, алгоритм Эль-Гамаля.

Введение

Для защиты информации применяются различные методы шифрования, меняющие с помощью криптографических преобразований исходный текст в нечитаемую последовательность символов. Рассматриваемая криптосистема Эль-Гамаля относится к схемам шифрования с открыты ключом. Для шифрования и расшифровки используются совершенно разные ключи. Ключ, используемый для преобразования исходного текста в шифротекст, разрешается передавать любому пользователю системы, не задумываясь о безопасности, поэтому этот ключ называют открытым. Другой ключ, который используют для восстановления исходного текста, называют секретным. Это позволяет свободно передавать и обменивать ключи по различным сетям с открытым доступом.

Предложенный Эль-Гамалем асимметричный алгоритм универсален. Его можно использовать для шифрования данных, для формирования цифровой подписи и для согласования общего ключа. Алгоритм также может быть модифицирован для схем проверки пароля и доказательства идентичности сообщения. Его безопасность основана на трудности вычисления дискретных логарифмов.

Основные определения

Введем некоторые определения, которые будут использованы в работе.

Полем называют коммутативное кольцо  с единицей, в котором любой элемент, отличный от нуля, имеет обратный, причем:

1.   – коммутативная группа с нейтральным элементом 0;

2.   – коммутативная группа c нейтральным элементом ;

3.  Умножение дистрибутивно относительно сложения:
.

Говорят, что два целых числа  и  сравнимы по модулю  и пишут , если  (разность и  делится на  без остатка). Множество всех чисел, сравнимых с  по модулю , называется классом вычетов  по модулю . Множество всех классов вычетов по модулю образует кольцо вычетов. В качестве операций сложения и умножения в этом кольце используются сложение и умножение по модулю.

Конечным полем  порядка  называется поле, состоящее из конечного числа элементов. Поле классов вычетов по простому модулю является конечным полем.

В конечном поле  для произвольных элементов  дискретным логарифмом числа  по основанию  называется натуральное число  такое, что . Задачу вычисления дискретного логарифма при заданных значениях  называют задачей дискретного логарифмирования в конечном поле.

Число , взаимно простое с , принадлежит показателю , если  – наименьшее натуральное число, для которого . Число, принадлежащее показателю функции Эйлера , называют первообразным (примитивным) корнем по модулю . Другими словами, первообразный корень – это образующий элемент мультипликативной группы кольца вычетов по модулю .

История алгоритма

Египетский криптограф Тахер Эль-Гамаль в 1985 году опубликовал статью «Криптосистема с открытым ключом и схема цифровой подписи на основе дискретных логарифмов» (“A Public key Cryptosystem and A Signature Scheme based on discrete Logarithms” [3]), где описаны алгоритмы создания ассиметричных систем шифрования и электронной цифровой подписи, базирующиеся на трудности вычисления дискретного логарифма.

Описание алгоритма

Т. Эль-Гамаль предложил следующую схему шифрования на основе возведения в степень по модулю большого простого числа.

              I.          Генерация ключей.

Первая часть протокола состоит в генерации ключей – открытого и закрытого.

Открытый ключ представляет собой тройку чисел . Генерируется большое простое число , по модулю которого будут осуществляться все дальнейшие сравнения: .

Замечание. В схемах шифрования в качестве модуля необходимо использовать большое целое простое число, имеющее в двоичном представлении длину 512–1024 бит.

Затем генерируется закрытый ключ  из условия, что его значение не должно превосходить : .

Выбирается первообразный корень по модулю . Затем вычисляется последний элемент открытого ключа.

Замечание. В работе используется алгоритм быстрого возведения в степень по модулю.

Сформированный открытый ключ рассылается по незащищенным каналам связи абонентам.

Замечание. Определение закрытого ключа на основе открытого невозможно даже на современном технологическом уровне.

           II.          Шифрование сообщения 

Абонент, желающий зашифровать сообщение, генерирует случайное натуральное взаимно простое с модулем  сессионное число : , причем , .

Вычисляются шифры  для каждого элемента сообщения:

;

.

Вся упорядоченная последовательность , состоящая из шифров элементов , является шифром сообщения (шифротекстом).

        III.          Расшифровка .

Зная закрытый ключ , исходное сообщение можно вычислить из шифротекста:

.

.

Замечание. Для удобства возведения в степень можно применить малую теорему Ферма. Так как , допускается умножить правую часть сравнения на .

Докажем, что :

,

,

,
,
.

Из условия  следует равенство.

Пример работы алгоритма

Пусть нескольким абонентам  необходимо передать сообщения  абоненту . Рассмотрим случай, когда передаваемая информация имеет кодируемый характер, а именно текстовое представление.

Абонент  формирует случайное простое число , по модулю которого будут производиться все сравнения. Для наглядности работы алгоритма выберем небольшое число: .

Также абонент    ─ первообразный корень по модулю : . Далее выбирается случайное натуральное число , меньшее  и не равное 1: . Затем вычисляется последняя составляющая открытого ключа : .

Открытый ключ  рассылается по незащищенным каналам связи, а секретный ключ  хранится абонентом  в тайне.

Получив открытый ключ, абоненты  на его основе шифруют сообщение. Рассмотрим процесс шифрования сообщения . Текстовая строка представляется как последовательный набор символов, который, в свою очередь, представляется кодовой комбинацией на основании таблицы ASCII: .

Далее каждая кодовая комбинация шифруется следующим образом:

1.  Выбирается случайный натуральный сессионный ключ , находящийся в диапазоне . Например, .

2.  Вычисляются пары чисел :  и .

Следовательно, для символа  шифр будет иметь вид 

Аналогичным образом при  и  соответственно символы  и  получат шифры  и .

Зашифрованное сообщение  отправляется абоненту .

Замечание. Наглядно видно, что недостатком данного метода шифрования является увеличение длины зашифрованного сообщения в два раза относительно исходного.

Получив зашифрованное сообщение, абонент  посимвольно расшифровывает текст: .

Аналогичным образом получим , .
Обратным преобразованием по таблице ASCII получим строку . Таким образом, абонент B расшифрует сообщение.

Пример программно-аппаратной реализации алгоритма

В процессе работы была создана одноранговая система передачи текстовых сообщений по сети Интернет с возможностью криптографической защиты передаваемых данных.

Рассмотрим основные алгоритмы программы: шифрование и дешифрование текстовых строк.

Функция шифрования текста последовательно каждому символу ставит в соответствие пару чисел, записывая их в адрес по указателю dcrp_message. Причем указатель message ссылается на строку, которую требуется зашифровать.

String^ dcrp_message = ""; //строка, содержащая зашифрованные данные

if (message->Length >0){// проверка строки на пустоту

array<Char>^ temp = gcnew array<Char>(message->Length - 1);

temp = message->ToCharArray(); // разбиение message на массив символов

for (int i=0; i <= message->Length - 1; i++){

unsigned int s = (unsigned int)temp[i]; // представление символа как числа

// генерация псевдослучайного числа в необходимом диапазоне

·     k = Random().Next(2, module-1);

·     unsigned int a = power(g, k, module); // 

·     unsigned int b = mul (power(publicKey, k, module ), s, module);
//

dcrp_message = dcrp_message + a + " " + b + " ";

  }

  message = dcrp_message;

}

Дешифрование происходит сложнее и требует большее количество операций. Переданный шифротекст является строкой вида , на которую указывает dcrp_msg.

// разбиение шифротекста сообщения на массив указателей

array<String^>^ strA = dcrp_msg->Split(' ');

if (strA->Length > 0){ // проверка на пустоту

  for (int i = 0; i < strA->Length - 1; i += 2){

//формирование массивов первых и вторых компонент шифров символов

·     array<Char>^ a = gcnew array<Char>(strA[i]->Length);

·     array<Char>^ b = gcnew array<Char>(strA[i+1]->Length);

·     unsigned int ai = 0;

·     unsigned int bi = 0;

·     a = strA[i]->ToCharArray();

·     b = strA[i + 1]->ToCharArray();

//преобразование компонент шифра

           for (int j = 0; (j < a->Length); j++)

                     ai = ai * 10 + (unsigned int)(a[j] - 48);

           for (int j = 0; (j < b->Length); j++)

                     bi = bi * 10 + (unsigned int)(b[j] - 48);

           if ((ai != 0) && (bi != 0)){

                     unsigned int deM = mul(bi, power(ai, module - 1 - privateKey, module), module); //.

                     Char m((unsigned int)deM); // представление числа как символа

                     msg = msg + m; // формирование расшифрованного сообщения

           }

  }

}

Пример работы ПО

В данном примере осуществляется передача конфиденциальной информации от пользователя Professor другому пользователю Assistant Professor, который генерирует секретный ключ . При этом Assistant Professor передает открытый ключ  собеседнику. Тот, в свою очередь, установив параметры открытого ключа, шифрует конфиденциальное сообщение. На данном примере видно, что длина сообщения возрастает.

Получив шифротекст сообщения, пользователь Assistant Professor дешифрует данные. Таким образом, информация передана по открытой сети Интернет с более высокой степенью защищенности при помощи криптографического алгоритма защиты.

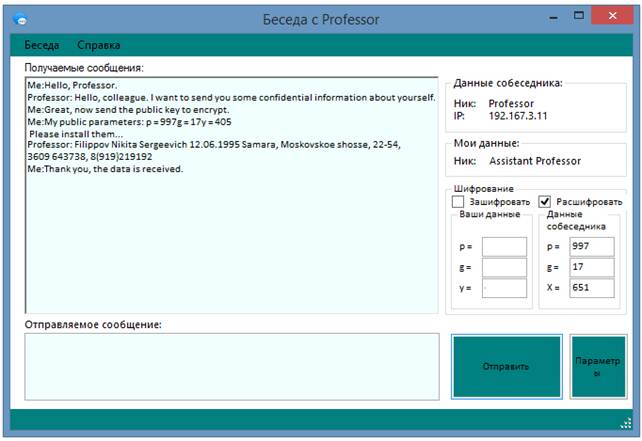
Рисунок 1. Диалоговое окно пользователя Assistant Professor

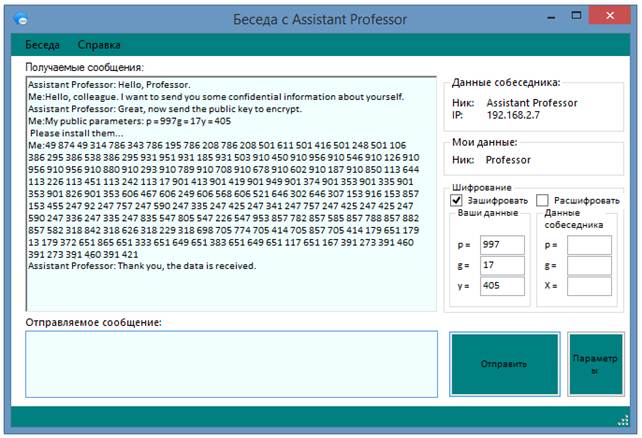
Рисунок 2. Диалоговое окно пользователя Professor

Рeзультaты и вывoды

Была разработана система, позволяющая безопасно передавать сообщения по незащищенному каналу связи между двумя абонентами. В её основе лежит алгоритм Эль-Гамаля, опирающийся на трудности вычисления дискретных логарифмов в конечном поле. Система может применяться и внедряться на местах, где значима безопасность и конфиденциальность передаваемой информации. Злоумышленник не сможет получить желаемые данные, так как для восстановления сообщения у него будет недостаточное количество составляющих для решения задачи расшифрования. Таким образом, созданная система является эффективным средством защиты от перехвата информации в открытом канале связи.