ЗАДАЧА ОБ ОЖЕРЕЛЬЯХ. АЛГОРИТМЫ НАХОЖДЕНИЯ РЕШЕНИЙ. ПРОГРАММНАЯ РЕАЛИЗИЦИЯ ЗАДАЧИ
Секция: 6. Математические науки

XXXIV Студенческая международная заочная научно-практическая конференция «Молодежный научный форум: технические и математические науки»
ЗАДАЧА ОБ ОЖЕРЕЛЬЯХ. АЛГОРИТМЫ НАХОЖДЕНИЯ РЕШЕНИЙ. ПРОГРАММНАЯ РЕАЛИЗИЦИЯ ЗАДАЧИ
Введение
В данной статье рассматриваются некоторые алгоритмы решения задачи об ожерельях. В данной работе уделим особое внимание Лемме Бёрнсайда, теореме Пойа и некоторым соответствующим определениям, так как этот теоретический материал поможет реализовать программный продукт решения задачи, что является нашей целью.
Актуальность
В чем же состоит актуальность выбранной нами темы? Ответ на данный вопрос прост. В теории кодирования некоторые вопросы связаны с известной комбинаторной задачей, которая называется «Задача об ожерельях».
Какое же отношение имеет задача об ожерельях к проблемам кодирования? А дело вот в чем: при передаче закодированных сообщений на передающей и приемной сторонах канала связи должна выполняться синхронизация. Синхронность работы обеспечивается тактовыми генераторами. При сбоях этих генераторов происходит нарушение синхронизации, а это в свою очередь приведет к неправильному восприятию символов. Т.е. в качестве начального символа кодового слова воспринимается такой символ, который и не является начальным. Отсюда вытекает и актуальность задачи построения кодов, которые способны восстанавливать синхронизацию.
Основные определения
Действие группы ![]() на множестве
на множестве ![]() – это гомоморфизм групп
– это гомоморфизм групп ![]() , где
, где ![]() – группа биекций
– группа биекций![]() . Обозначается
. Обозначается ![]() .
.
При фиксированном действии ![]() для каждого элемента
для каждого элемента ![]() определены его орбита
определены его орбита ![]() и стабилизатор – подгруппа
и стабилизатор – подгруппа ![]() .
.
Орбиты действия – классы эквивалентности по отношению
![]() .
.
Действие ![]() называется
называется
· Транзитивным, если все множество ![]() – единственная орбита, т.е.
– единственная орбита, т.е. ![]() ;
;
· Эффективным, если его ядро неэффективности ![]() тривиально.
тривиально.
Функция Эйлера ![]() определяется для всех целых положительных a и представляет собою число чисел ряда
определяется для всех целых положительных a и представляет собою число чисел ряда ![]() взаимно простых с a.
взаимно простых с a.
Инвариантной перестановкой будет являться любая перестановка, полученная из данной циклическим сдвигом.
Перестановка – это упорядоченный набор чисел ![]() , обычно трактуемый как биекция на множеств
, обычно трактуемый как биекция на множеств ![]() , которая числу
, которая числу ![]() ставит в соответствие i-ый элемент из набора. Число
ставит в соответствие i-ый элемент из набора. Число ![]() при этом называется порядком перестановки.
при этом называется порядком перестановки.
Циклом длины ![]() называется такая перестановка
называется такая перестановка ![]() которая тождественна на всём множестве X кроме подмножества
которая тождественна на всём множестве X кроме подмножества ![]() и
и ![]() ,
, ![]() . Обозначается
. Обозначается ![]()
Формулировка задачи об ожерельях
Требуется посчитать количество ожерелий из ![]() бусинок, каждая из которых может быть покрашена в один из
бусинок, каждая из которых может быть покрашена в один из ![]() цветов. При сравнении двух ожерелий их можно поворачивать, но не переворачивать, т.е. разрешается сделать циклический сдвиг. Решение данной задачи опирается на лемму Бёрнсайда и теорему Пойа.
цветов. При сравнении двух ожерелий их можно поворачивать, но не переворачивать, т.е. разрешается сделать циклический сдвиг. Решение данной задачи опирается на лемму Бёрнсайда и теорему Пойа.
Лемма Бёрнсайда
Пусть группа ![]() действует на множество
действует на множество ![]() . Будем называть два элемента
. Будем называть два элемента ![]() и
и ![]() эквивалентными. Если
эквивалентными. Если ![]() для некоторого
для некоторого ![]() , то два элемента
, то два элемента ![]() и
и ![]() являются эквивалентными. Тогда число классов эквивалентности равно сумме числа стабилизаторов по всем элементам группы
являются эквивалентными. Тогда число классов эквивалентности равно сумме числа стабилизаторов по всем элементам группы ![]() , делённой на размер этой группы:
, делённой на размер этой группы: ![]() ,
, ![]() — количество стабилизаторов для элемента
— количество стабилизаторов для элемента ![]() .
.
Обобщением леммы Бёрнсайда является Теорема Пойа. Она позволяет находить количество классов эквивалентности, используя величину - количество циклов в перестановке.
Теорема Пойа
![]() где
где ![]() — количество различных классов эквивалентности,
— количество различных классов эквивалентности, ![]() - количество циклов в перестановке
- количество циклов в перестановке ![]() ,
, ![]() - количество различных состояний одного элемента.
- количество различных состояний одного элемента.
Первый алгоритм нахождения решения задачи про ожерелья
Дано: бусины ![]() различных цветов, ожерелье состоит из
различных цветов, ожерелье состоит из ![]() бусин.
бусин.
Для решения данной задачи мы обратимся к теореме Пойа, воспользовавшись нижеприведенной формулой: 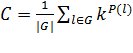
Из условия видно, что любая перестановка, которая получается путем циклического сдвига, будет инвариантной данной. Очевидно, что всего инвариантных перестановок в каждом классе ![]() (т.к. для каждой перестановки длины
(т.к. для каждой перестановки длины ![]() существует
существует ![]() инвариантная перестановка). Следующим шагом будет нахождение
инвариантная перестановка). Следующим шагом будет нахождение ![]() . Обратим внимание, что в i-ой перестановке на позиции
. Обратим внимание, что в i-ой перестановке на позиции ![]() стоит элемент
стоит элемент ![]() . А также видим, что элемент
. А также видим, что элемент ![]() переходит в элемент
переходит в элемент ![]() , где
, где ![]() . Следовательно, длина цикла для -ой перестановки равна
. Следовательно, длина цикла для -ой перестановки равна 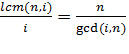 , где
, где ![]() -НОД
-НОД![]() ,
,![]() НОК
НОК![]() .
.
Откуда следует что: 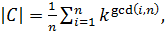 где
где ![]() — количество различных ожерелий, получаемые из
— количество различных ожерелий, получаемые из ![]() бусин
бусин ![]() различных цветов.
различных цветов.
Если бусины раскрашиваем в один цвет, то они принадлежат одной орбите, т.е. одна получается из другой путем преобразования симметрии. У тождественного поворота есть ![]() неподвижных точек. Обратившись к лемме Бёрнсайда, получаем, что число орбит равняется
неподвижных точек. Обратившись к лемме Бёрнсайда, получаем, что число орбит равняется 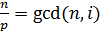 , где
, где ![]() - минимальное число, причем
- минимальное число, причем ![]() делится на
делится на ![]() , число их раскрасок
, число их раскрасок ![]() . Сумма инвариантных раскрасок для всех поворотов:
. Сумма инвариантных раскрасок для всех поворотов: ![]()
В последней сумме ![]() слагаемых (
слагаемых (![]() — функция Эйлера), для которых
— функция Эйлера), для которых ![]() . Если же
. Если же ![]() , то
, то 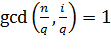 .
.
Количество ![]() , меньших
, меньших ![]() , определяется перебором чисел вида
, определяется перебором чисел вида 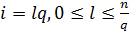 , и обязательно проверяются эти числа условием
, и обязательно проверяются эти числа условием 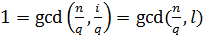 .
.
По определению функции ![]() таких чисел будет
таких чисел будет ![]() . Сделав подстановку, получаем:
. Сделав подстановку, получаем: 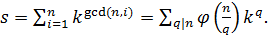 Тогда количество различных
Тогда количество различных
ожерелий будем высчитывать по формуле: 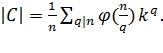
Второй алгоритм нахождения решения про ожерелья
Пусть теперь ожерелья считаются одинаковыми, они переходят друг в друга не только поворотом, но и отражением относительно некоторой оси, которая может располагаться на двух противоположных бусин, или ось лежит на противоположных пустотах, а также ось может проходить через бусину, если их нечетное количество. Для решения задачи по второму алгоритму будем пользоваться леммой Бёрнсайда.
Сначала отметим, что в качестве операций требуется рассматривать только повороты и отражения. Возможные операции:
1) Поворот и отражение – отражение.
2) Отражение и поворот – отражение.
3) Отражение и отражение – поворот.
Пронумеруем наши бусинки по часовой стрелке. Поворот не меняет порядка. Нетрудно понять, что и отражение не меняет порядка, а меняет лишь направление обхода бусин. Если мы сначала совершим поворот, а потом проведем отражение относительно какой-нибудь оси, то мы можем получить, то же самое и обычным отражением относительно какой-то оси. Такая ось будет, ведь всегда можно выбрать ось, которая поставит первую бусину на своё первоначальное место, поменяв направление обхода. Поэтому поворот и отражение не добавляет нам новой операции. Аналогично рассуждая во втором пункте, получим такой же вывод. В третьем пункте мы дважды меняем направление обхода, но не изменяем порядка. Поэтому эту операцию заменит обычный поворот.
Выделим два случая, когда число бусин нечетное и четное.
Случай 1. Дано: число бусин - нечётное. Тогда мы имеем ![]() осей, которые проходят через каждую бусину. Рассмотрим одну ось. Возьмём саму бусину, через которую проходит выбранная ось, и половину бусин с одной стороны от этой оси. Окрасим выбранные бусины в различные цвета, а остальная половина бусин по ним однозначно восстановится. Таким образом, количество неподвижных точек для одной оси получим
осей, которые проходят через каждую бусину. Рассмотрим одну ось. Возьмём саму бусину, через которую проходит выбранная ось, и половину бусин с одной стороны от этой оси. Окрасим выбранные бусины в различные цвета, а остальная половина бусин по ним однозначно восстановится. Таким образом, количество неподвижных точек для одной оси получим ![]() . Операций в группе станет в два раза больше:
. Операций в группе станет в два раза больше: ![]() (т.е.
(т.е.![]() сдвигов и
сдвигов и ![]() отражений).
отражений).
Воспользуемся леммой Бёрнсайда, взяв формулу: ![]()
![]() . Первые
. Первые ![]() операций — повороты, сумма их количества неподвижных точек принимает значение
операций — повороты, сумма их количества неподвижных точек принимает значение ![]() , где
, где ![]() - количество ожерелий из
- количество ожерелий из ![]() бусинок
бусинок ![]() различных цветов без отражений (вышеприведенный алгоритм). Деление в предыдущем алгоритме происходило на
различных цветов без отражений (вышеприведенный алгоритм). Деление в предыдущем алгоритме происходило на ![]() , а здесь на
, а здесь на ![]() . Следующие
. Следующие ![]() операций — отражения. Сумма неподвижных точек будет
операций — отражения. Сумма неподвижных точек будет ![]() .
.
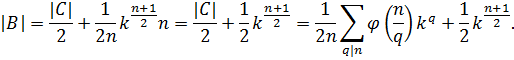
Случай 2. Дано: число бусин - чётное. В данном случае мы имеем ![]() осей, проходящих через пустоты между бусинами. Можно выбрать по
осей, проходящих через пустоты между бусинами. Можно выбрать по ![]() бусин и дать им различные цвета. Остальная половина восстановится по ним. Для данных осей количество неподвижных точек будет
бусин и дать им различные цвета. Остальная половина восстановится по ним. Для данных осей количество неподвижных точек будет ![]() . Ещё у нас есть
. Ещё у нас есть ![]() осей, проходящих через бусины. В данных случаях мы можем выбрать по
осей, проходящих через бусины. В данных случаях мы можем выбрать по ![]() бусин. То есть количество неподвижных точек будет
бусин. То есть количество неподвижных точек будет ![]() . Операций в группе также
. Операций в группе также ![]() . Снова воспользовавшись Леммой Бёрнсайда, получим:
. Снова воспользовавшись Леммой Бёрнсайда, получим:
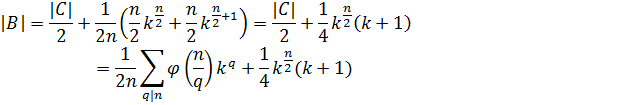
Теперь вернемся к проблемам кодирования. Разложим ![]() бусин по окружности, указав для каждой бусины номер ее цвета. Если совершить обход этой окружности в определенном направлении, начав с какой-то бусины, то ожерелью из
бусин по окружности, указав для каждой бусины номер ее цвета. Если совершить обход этой окружности в определенном направлении, начав с какой-то бусины, то ожерелью из ![]() бусинок будет соответствовать слово (
бусинок будет соответствовать слово (![]() ), где
), где ![]() - это номер цвета i-й бусины. Т.к. обход можно начать с любой бусины, поэтому любому ожерелью соответствует
- это номер цвета i-й бусины. Т.к. обход можно начать с любой бусины, поэтому любому ожерелью соответствует ![]() слов, получаемых одно из другого путем циклических сдвигов. Чтобы вывести формулу для нахождения числа основных слов, воспользуемся функцией Мёбиуса
слов, получаемых одно из другого путем циклических сдвигов. Чтобы вывести формулу для нахождения числа основных слов, воспользуемся функцией Мёбиуса
![]() , если
, если ![]() ;
;
![]()
![]()
0 - в остальных случаях.
Обозначив общее число основных слов длины ![]() алфавита из
алфавита из ![]() символов
символов ![]() ,получим
,получим ![]() . Полученная формула позволяет найти число интересующих нас ожерелий, которое, очевидно, равно
. Полученная формула позволяет найти число интересующих нас ожерелий, которое, очевидно, равно ![]()
Один из возможных путей решения - рассмотрение множества n-буквенных кодовых слов, удовлетворяющего такому ограничению: если (![]() ) и (
) и (![]() )- кодовые слова, то никакое из «перекрытий» между ними
)- кодовые слова, то никакое из «перекрытий» между ними
(![]() ), (
), (![]() ),…, (
),…, (![]() ) не является кодовым словом. Коды, обладающие этим свойством, называются синхронизируемыми. Решение задачи об ожерельях позволит узнать, насколько велика плата за усовершенствование кода. Действительно, если
) не является кодовым словом. Коды, обладающие этим свойством, называются синхронизируемыми. Решение задачи об ожерельях позволит узнать, насколько велика плата за усовершенствование кода. Действительно, если ![]() - кодовое слово синхронизируемого кода, то кодовым словом не может быть его циклический сдвиг, так как он является перекрытием для пары
- кодовое слово синхронизируемого кода, то кодовым словом не может быть его циклический сдвиг, так как он является перекрытием для пары ![]() .
.
Следовательно, обозначенное ![]() максимальное число n-буквенных слов синхронизируемого кода, который использует алфавит из
максимальное число n-буквенных слов синхронизируемого кода, который использует алфавит из ![]() символов, не превосходит числа несоставных ожерелий с
символов, не превосходит числа несоставных ожерелий с ![]() бусинами
бусинами ![]() различных цветов.
различных цветов.
![]() .
.
В итоге, получаем верхнюю границу для числа n -буквенных кодовых слов синхронизируемого кода: ![]()
Реализация программного продукта
Формулировка конкретной задачи: ожерелье состоит из N колечек, нанизанных на замкнутую нить. Все колечки имеют разные размеры. В зависимости от размера колечки пронумерованы числами от 1 до N, начиная с самого маленького и до самого большого. Колечки можно передвигать вдоль нити и протаскивать одно через другое, если номера этих колечек отличаются более чем на единицу. Необходимо упорядочить колечки в порядке возрастания номеров вдоль нити по часовой стрелке.
Реализация решения данной задачи разработана на языке программирования С++. Среда разработки - Microsoft Visual Studio.
class Functions{
public:
static int ReadInt(){
int value = 0;
scanf("%d", &value);
return value;}
static int Abs(int x)
{return (x < 0) ? -x: x;}
};
class Data{
private: …
public: …
bool Swap(int i, int j){
Data &data = *this;
if (Functions::Abs(data[i]-data[j]) < 2)
return false;
int t = data[i];
data[i] = data[j];
data[j] = t;
return true;}
…
class Solver{
public:
static void Solve(Data &data){
while (true){
bool end = true;
for (int i = 0; i < data.Size(); i++){
if (data[i] > data[i+1])
continue;
if (data.Swap(i, i+1)){
printf("%d %d\n", data[i+1], data[i]);
end = false;}
} if (end)
break;
}printf("0\n");
};}; …
Заключение
Таким образом, в данной работе мы достигли своей цели, представив программную реализацию решения конкретной задачи об ожерельях, а также рассмотрели различные алгоритмы нахождения решения.





