ЗОЛОТАЯ ТЕОРЕМА БЕРНУЛЛИ
Секция: 6. Математические науки

XXXIV Студенческая международная заочная научно-практическая конференция «Молодежный научный форум: технические и математические науки»
ЗОЛОТАЯ ТЕОРЕМА БЕРНУЛЛИ
Кабардино-Балкарская республика относится к региону с богатыми природными и социально-демографическими предпосылками развития сельскохозяйственной отрасли. Республике нужны грамотные работники. Специалисты сельского хозяйства, в частности агрономы, зоотехники, технологи, ветеринары и т.д. Специалисты, владеющие не только сельскохозяйственными специальностями, но и знающие законы физики, генетики, биологии, химии, экономики. Все эти науки в той или иной мере используют математику, что в очередной раз свидетельствует в пользу серьезного изучения этой дисциплины.
Я студентка 1-го курса Кабардино-Балкарского государственного аграрного университета, будущий технолог. При изучении дисциплины высшая математика меня очень заинтересовал раздел теория вероятностей.
Многие явления в окружающем нас мире, в частности в сельском хозяйстве носят случайный характер. Если мы с явлением сталкиваемся один раз, мы не можем его точно предсказать в следующий раз. Но если это явление можно наблюдать несколько раз, при неизменных условиях, то оказывается данное явление можно описать с помощью формул. Так, например, если посеять одно зерно, мы не можем говорить, взойдет оно или нет. Однако, если наблюдение повторить несколько раз, то можно проследить некоторую закономерность. При посеве зерен, давших всход, к общему числу посеянных с возрастанием их числа будет мало отличаться от некоторого постоянного числа. Такие эксперименты еще называются схемой повторных независимых испытаний или схемой Бернулли.
Якоб Бернулли поставил задачу: можно ли определить теоретическую вероятность по результатам испытаний и посвятил изучению этой особенности несколько десятилетий. Он доказал ее математически, т.е. например, при бросании игрального кубика большое количество раз, доля случаев, когда выпадет три очка, будет приближаться к 1/6. Математик назвал свое открытие золотой теоремой, однако в современной формулировке она известна как закон больших чисел [2,с.283].
Важно помнить о главном условии при решении задач при помощи схемы Бернулли – это постоянство. Без этого схема теряет всякий смысл. Если условия у нас постоянны, то мы можем точно определить требуемую вероятность, что событие А произойдет ровно m раз из n возможных. Якоб Бернулли сформулировал теорему, которая носит его имя. «Теорема Бернулли» является одной из главных теорем в теории вероятности. Впервые она опубликована в труде Я. Бернулли «Искусство предложений». Рассмотрим ее суть. Проведем n испытаний Бернулли, то есть таких испытаний, когда все n испытаний независимы, вероятность появления события А в каждом отдельно взятом или единичном испытании постоянна и от испытания к испытанию не изменяется. Обозначим вероятность появления события А в единичном испытании буквой р, а вероятность противоположного события – буквой q=1−p. Тогда вероятность того, что событие А появится в этих n испытаниях ровно m раз, выражается формулой Бернулли [1,с.37]:
 (1)
(1)
На практике нам часто приходится сталкиваться с такими задачами, которые можно представить в виде многократно повторяющихся испытаний, в результате каждого из которых может появиться или не появиться событие A. При этом интерес представляет исход не каждого отдельного испытания, а общее количество появлений события A в результате определенного количества испытаний. В подобных задачах нужно уметь определять вероятность любого числа m появлений события A в результате n испытаний. Рассмотрим случай, когда испытания являются независимыми и вероятность появления события A в каждом испытании постоянна. Такие испытания называются повторными независимыми.
Примером независимых испытаний может служить проверка на годность изделий, взятых по одному из ряда партий. Если в этих артиях процент брака одинаков, то вероятность того, что отобранное изделие будет бракованным, в каждом случае является постоянным числом.
Современные ученые пытаются доказать, что «Формула Бернулли» не соответствует законам природы и можно решить задачи, не применяя ее к исследованию. Конечно, это возможно, большинство задач по теории вероятности, возможно, выполнить и без формулы Бернулли, главное не запутаться в больших объемах цифр и информации.
При практическом применении теории вероятностей часто приходится встречаться с задачами, в которых одно и то же испытание повторяется неоднократно. В результате каждого испытания может появиться или не появиться некоторое событие А, причем нас не интересует результат каждого отдельного испытания, а нас интересует общее число появлений события А в результате серии опытов. Например, если производится защита сельскохозяйственных угодий от выпадения града и крупного дождя. Противоградовой службой осуществляется ряд выстрелов по опасным кучевым облакам, на основе данных метеорологических служб. Выстрелы производятся из одного и того оружия, с одной и той же вероятностью попадания. В данной ситуации нас интересует наивероятнейшее число попаданий. От этого зависит наш будущий урожай и безопасность населения. Такие задачи достаточно решаемы в случае, когда испытания являются независимыми.
Остановимся на следствии из формулы Бернулли - нахождении наиболее вероятных событий.
Число успехов m0, которому при заданном n соответствует максимальная биномиальная вероятность Pn(m0), называется наиболее вероятным числом успехов.
Для нахождения наиболее вероятного числа успехов m0 по заданным n и р можно воспользоваться неравенствами:
 . (2)
. (2)
Числа 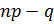 и
и  отличаются на единицу. Поэтому, если
отличаются на единицу. Поэтому, если 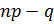 – дробное число, то
– дробное число, то  – также дробное и неравенство (2) определяет одно m0. Если
– также дробное и неравенство (2) определяет одно m0. Если 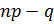 – целое число, то и
– целое число, то и  – также целое, тогда числа m0 и m0+1 будут иметь равную и наибольшую вероятность.
– также целое, тогда числа m0 и m0+1 будут иметь равную и наибольшую вероятность.
Подводя итоги сказанному, мы хотим привести несколько примеров:
Пример 1. Допустим, что на опытной делянке посеяно 15 семян. Пусть всхожесть всех семян одинакова и равна 80%. Возможны следующие элементарные события:
A0 - число семян, давших росток, равно 0;
A1 - число взошедших семян равно 1;
A2 - число взошедших семян равно2;
и т.д. и наконец,
A15 - все семена дадут всходы.
Как найти вероятности этих событий, в частности, вычислить вероятность того, что из 15 посеянных семян взойдет ровно 12, безразлично в какой последовательности?
Решение:
Число посеянных семян равно числу независимых испытаний, т.е. n= 15, число давших всходы m=12, p=0,8, q=1-0,8=0,2. Тогда
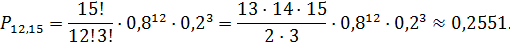
Событие «12» из «15» имеет небольшую вероятность.
Пример 2. В течение февраля месяца десять коров должны отелиться. Допустим, что в приплоде будет 1 теленок. Условимся, что вероятность рождения бычка от каждой коровы постоянна и равна 0,5. Конечно, данное предположение условно. Реально то, что каждое конкретное животное имеет не одинаковые возможности, в том числе и возможность дать в приплоде бычка или телочку. Рассмотрим осуществление следующих событий:
A0 - число родившихся бычков равно 0, все 10 телочки;
A1 - число родившихся бычков равно 1, остальные 9 телочки;
и т.д. и, наконец,
A10 - число родившихся бычков равно 10 и ни одной телочки.
Найдем, например, вероятность того, что в 10 отелах число родившихся бычков 7, а телочек 3.
Решение:
Число наблюдаемых коров принимаем равным числу независимых испытаний, т.е. n= 10, m= 7, p=0,5, q= 0,5. Находим
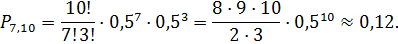
В заключение хотелось бы еще раз отметить, что Формула Бернулли дает точное значение вероятности того, что событие А наступит ровно m раз в n независимых испытаниях, определяемых схемой Бернулли. Однако, практическое применение этой формулы часто оказывается затруднительным, если числа m и n достаточно велики, а вероятность р – мала. Для этих целей существуют некоторые асимптотические приближения формулы Бернулли.





