ВЫБОР СASE– СРЕДСТВ МЕТОДОМ АНАЛИЗА ИЕРАРХИЙ

Аннотация. В статье описывается выбор CASE– средства методом анализа иерархий. Даются основные определения информационной системы, CASE–средства, метода анализа иерархий. А также описывается поэтапный расчет выбора по данному методу.

Ключевые слова: информационная система, проектирование, CASE– средства, метод анализа иерархий (МАИ), ARIS Tools, Silverrun, Rational Rose.

Тенденции развития информационных технологий сегодня диктуют новый уровень сложности востребованных информационных систем (ИС). Для успешной реализации проекта объект проектирования (ИС) должен быть прежде всего адекватно описан, должны быть построены полные и непротиворечивые функциональные и информационные модели. Такого рода разработка ИС не возможна в полной мере своей эффективности без использования CASE-средств.

Под термином CASE-средства понимаются программные средства, поддерживающие процессы создания и сопровождения ИС, включая анализ и формулировку требований, проектирование прикладного ПО (приложений) и баз данных, генерацию кода, тестирование, документирование, обеспечение качества, конфигурационное управление и управление проектом, а также другие процессы [1].

Современный рынок программных средств насчитывает около 300 видов различных CASE-средств. Поэтому основной задачей становится выбор максимально функционального и эффективного CASE– средства, например, на основе метода анализа иерархий (МАИ) американского ученого Томаса Саати. Данный метод является математическим инструментом системного подхода к сложным проблемам принятия решений.

МАИ – математический инструмент системного подхода к сложным проблемам принятия решений. МАИ не предписывает лицу, принимающему решение, какого-либо «правильного» решения, а позволяет ему в интерактивном режиме найти такой вариант (альтернативу), который наилучшим образом согласуется с его пониманием сути проблемы и требованиями к ее решению [2].

Алгоритм применения метода следующий:

1.  Определение иерархий целей;

2.  установление приоритетов критериев методом попарного сравнения;

3.  установление приоритетов альтернатив по каждому критерию;

4.  определение глобального приоритета альтернатив.

Иерархическая структура — это графическое представление проблемы в виде перевернутого дерева, где каждый элемент, за исключением самого верхнего, зависит от одного или более выше расположенных элементов (Рисунок 1).

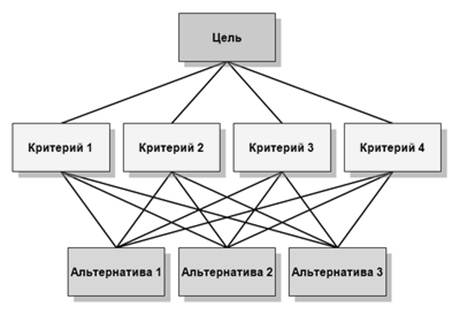
Рисунок 1. Схема метода анализа иерархий (иерархическая структура)

I этап – Составление иерархии целей.

Цель – Выбор наиболее эффективного CASE-средства для проектирования информационной системы (ИС).

Проанализировав большинство CASE-средств были выбраны следующие критерии выбора и наиболее подходящие для поставленной цели альтернативы.

Определение критериев выбора:

1.  Поддержка полного жизненного цикла ИС;

2.  простота освоения и использования CASE–средства;

3.  обеспечение качества проектной документации;

4.  использование общепринятых, стандартных нотаций и соглашений.

Определение альтернатив (CASE-средств):

A.Silverrun;

B. ARIS Toolset;

C. Rational Rose.

II этап – Установление приоритетов критериев.

На данном этапе формируем матрицу попарных сравнений критериев. В таблице 1 представлена шкала предпочтений объектов, необходимых для описания степени превосходства.

Далее проводим ранжирование критериев, которая включает в себя оценку компонент собственного вектора каждого критерия (формула 1) и нормализацию оценок (формула 2). А также проведем оценку согласованности матрицы, формулы 3-6.

Таблица 1.

Шкала относительной важности критериев

Если при сравнении одного вида деятельности с другим получено одно из вышеуказанных чисел, то при сравнении второго вида деятельности с первым получим обратную величину.

Ранжирование критериев.

·     Оценка компонент собственного вектора каждого критерия:

                                                              (1)

·     Нормализация оценок:

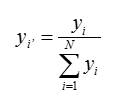                                                     (2)

где: y _iн показывает вклад каждого критерия в достижение цели.

Оценка согласованности матрицы.

1)  Вычисление максимального собственного числа матрицы (λ_max)

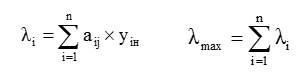              (3,4)

2)  Вычисление индекса согласованности (ИС)

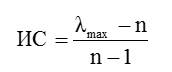                                           (5)

3)  Вычисление оценки согласованности (ОС)

ОС = ИС/ СС                                             (6)

Таблица 2.

Значения случайной согласованности (СС)

ОС ≤ 0,1                матрица согласованна

0,1<ОС ≤ 0,2        согласованность матрицы приемлема

ОС > 0,2               согласованность матрицы не приемлема

Расчеты представим в таблица 3,4. Расчеты производятся по формулам представленные выше (Формулы 1–6). На основании данных каждой таблицы произведем оценку согласованности мнений лица, принимающего решение (ЛПР).

Таблица 3.

Матрица попарных сравнений критериев

Таблица 4.

Матрицы попарных сравнений альтернатив по i-му критерию

Чтобы принять окончательное решение по выбору CASE– средства, необходимо значения векторов приоритета из всех таблиц по каждому фактору перенести в итоговую таблицу и рассчитать глобальный приоритет.

Глобальный приоритет определяется путем суммирования произведений значимости критерия (таблица 3) на вектор приоритета критерия по каждому CASE– средству (таблицы 4).

Таблица 5.

Итоговая матрица определения глобального приоритета альтернатив

Определение глобального приоритета определяется по формуле 7.

A_opt=max A_i                                                                                 (7)

Сравнивая полученные значения, определяется рейтинг CASE– средств. Высокий рейтинг будет соответствовать наибольшему значению глобального вектора приоритета. Согласно исходным данным наибольший приоритет оказался у CASE– средства Rational Rose.

С помощью данного метода можно обосновать выбор CASE-средства необходимого для проектирования информационной системы.

Одним из основных достоинств метода МАИ, является направленность на сравнение реальных альтернатив. Отмечу, что метод МАИ может применятся и в тех случаях, когда эксперты (или ЛПР) не могут дать абсолютные оценки альтернатив по критериям, а пользуются более слабыми сравнительными измерениями.

Одним из существенных недостатков метода МАИ, является то, что введение новой, недоминирующей альтернативы, критерия, или ЛПР может в общем случае привести к изменению предпочтений между ранее заданными альтернативами.