НЕПРЕРЫВНОЕ ВЕЙВЛЕТ-ПРЕОБРАЗОВАНИЕ В MATLAB

Статья посвящена непрерывному вейвлет-преобразованию и его применению при анализе различных одномерных сигналов с применением системы MATLAB.

Wavelet переводится с английского как «короткая волна». Вейвлеты находят широкое применение при анализе различных сигналов: аудиосигналов, биомедицинских сигналов, таких как: электрокардиограмма [1], электроэнцефалограмма [6] и др.

Прямое непрерывное вейвлет-преобразование сигнала s(t) задается путем вычисления коэффициентов по формуле:

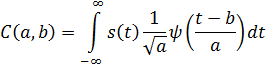
где: b – сдвиг, а – масштаб, а  – материнский вейвлет.

Прямое непрерывное вейвлет-преобразование позволяет получить график вейвлет-спектрограммы. На рис. 1 приведен пример непрерывного вейвлет-преобразования зашумленной синусоиды и его вейвлет-спектрограмма. При этом использовался вейвлет Добеши 4 (рис. 2).

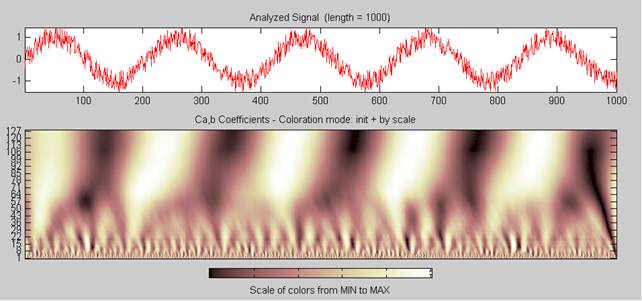
Рисунок 1. График зашумленной синусоиды и вейвлет-спектрограмма

Как следует из рис. 1, вейвлет-спектрограмма позволяет отразить локальные изменения сигнала. Высокочастотные составляющие сигнала соответствую малым значениям масштаба, а низкочастотные – большим значениям.

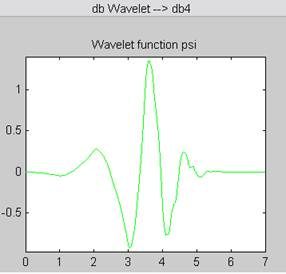
Рисунок 2. Вейвлет Добеши 4

Вейвлет-спектрограмма может быть построена или путем написания кода в командной строке, или с использованием пакета расширения Wavelet ToolBox. Данный пакет расширения обладает большим функционалом. Помимо построения графика вейвлет-спектрограммы, он также позволяет выводить графики анализируемого сигнала, выбирать базисный вейвлет и число масштабных коэффициентов.

На рис. 3 представлено рабочее окно пакета расширения Wavelet ToolBox, где:

A.Область отображения графической информации.

B. Панель управления графиками.

C. Информация об анализируемом сигнале и используемом вейвлете.

D.Панель управления преобразованием.

E. Окно выбора выводимых спектрограмм.

F.  Окно выбора стиля представления спектрограмм.

Рисунок 3. Окно графического интерфейса непрерывного преобразования в ToolBox MATLAB

Обратное непрерывное вейвлет-преобразование выполняется по формуле реконструкции:

где: 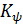 – константа, определяемая функцией .

Рассмотрим возможность применения вейвлетов при анализе различных сигналов.

Вейвлеты широко применяются при анализе аудиосигналов. Ученые с успехом применили вейвлеты для улучшения звучания старых грампластинок [8].

Вейвлеты также могут примениться при изучении климата [8]. Анализ выполняется на основе построенной вейвлет-спектрограммы.

Вейвлет-анализ широко используется при анализе биомедицинских сигналов. Значительное число работ посвящено исследованию электрокардиограмм и электроэнцефалограмм с применением непрерывного вейвлет-преобразования [2, 3, 6].

MATLAB предоставляет широкие возможности не только для выполнения моделирования алгоритмов цифровой обработки сигналов с использованием непрерывного вейвлет-преобразования, но и позволяет упростить реализацию на цифровых сигнальных процессорах [2, 5].