ИССЛЕДОВАНИЕ ВОЗМОЖНОСТЕЙ ГЕНЕТИЧЕСКИХ АЛГОРИТМОВ НА ПРИМЕРЕ РЕШЕНИЯ ЗАДАЧИ КОММИВОЯЖЕРА

Аннотация. В статье на примере задачи коммивояжера исследованы возможности генетических алгоритмов при решении задач оптимизации. Для этого разработан алгоритм, основанный на стратегии направленной эволюции. В алгоритме применяются различные комбинации генетических операторов в зависимости от длины цепочки поколений, в которых лучший уровень приспособленности не меняется.

Введение. Существует класс задач, решение которых сложно или невозможно представить в формализованном виде. Некоторые задачи не решаются с помощью традиционных алгоритмов за приемлемое время. Использование генетических алгоритмов позволяет решить эти проблемы. Кроме этого, генетические алгоритмы адаптивны, могут быть распараллелены, легко комбинируются с нейронными сетями и элементами нечеткой логики.

Постановка задачи. Постановка задачи коммивояжера в виде модели на графе формулируется следующим образом.

Имеется полный, взвешенный, неориентированный граф

G = (V, E),

где: V – множество вершин графа, соответствующих городам, |V|=N – количество городов;

E – множество рёбер графа, соответствующих путям сообщений между городами. Каждому ребру сопоставляется вес или критерий оптимальности пути.

Решением задачи является гамильтонов цикл наименьшего веса.

Необходимо разработать генетический алгоритм, который эффективно решал бы поставленную задачу.

Генетический алгоритм. Одним из предварительных этапов разработки генетического алгоритма является представление решения задачи в формальном виде. При этом нужно определить такую структуру, с помощью которой можно будет кодировать любое возможное решение, а также получать новые решения. Доказано, что идеальной структуры представления нет, поэтому эта задача решается эмпирическим путем.

В данной работе решение задачи представляется вектором вида:

V = (v₁, v₂, v₃,…, v_n),

где: n – количество вершин, v_i – вершина графа.

Способ представления решения задачи в закодированном виде должен позволять легко производить оценку его пригодности. Очевидным решением является кодирование решения в виде массива из n неповторяющихся чисел:

m = a₁ a₂ a_{3 …} a_n,

где: n – количество вершин, a_i – номер вершины, а индекс i – порядок обхода графа.

Для оценки пригодности решения необходимо разработать фитнесс-функцию. Нельзя представить в качестве результата работы функции вес гамильтонова цикла. Чем меньше вес, тем лучше решение, однако результат фитнесс-функции должен быть выше при лучших решениях. Поэтому в качестве фитнесс-функции выбрана следующая функция:

fitness = 200*N – g,

где: 200 – средний вес ребра, N – количество вершин графа, g – вес гамильтонова цикла. Получается, что 200*N – вес потенциально худшего решения. Это значение было выбрано, чтобы результат работы фитнесс-функции не был отрицательным. В противном случае это может негативно отразиться на работе оператора селекции.

В качестве оператора скрещивания взят классический упорядоченный оператор кроссинговера. Его суть заключается в следующем:

1)  выбираются две родительские особи;

2)  в особь-потомок копируется половина хромосомы одной родительской особи;

3)  просматриваются все гены второй особи по порядку, и если ген отсутствует в особи-потомке, то он добавляется к потомку.

Данный выбор обусловлен тем, что он предотвращает повтор генов при скрещивании. Повтор генов нежелателен, так как рассматривается гамильтонов цикл.

В алгоритме реализовано три оператора мутации.

Мутация 1. Случайным образом выбираются два гена, и затем они меняются местами.

Мутация 2. Случайным образом выбираются 4 точки:

a₁∈[0, N/4], a₂∈[N/4, N/2], a₃∈[N/2, 3N/4], a₄∈ [3N/4, N].

Затем два отрезка хромосом ch1=(v_a1, v_a1+1, …, v_a2) и ch2 =(v_a3, v_a3+1, …, v_a4) меняются местами_.

Мутация 3. Случайным образом меняет местами все гены:

∀(v ∈ V) swap(v, v_rand),

где: swap() – функция обмена местами двух генов, V – множество всех вершин графа, v_rand – случайная вершина

При выборе оператора селекции была поставлена задача сохранения многообразия особей, не теряя при этом лучшие. Стандартные операторы селекции не могут в полной мере выполнить эти условия, поэтому был создан комбинированный оператор селекции. Когда из M особей нужно отобрать N, то сначала методом элитной селекции отбирается N/20+1 особей. Затем оставшиеся особи отбираются с помощью колеса рулетки.

Кроме основных генетических операторов были созданы дополнительные операторы управления популяцией, чтобы реализовать направленную эволюцию. К ним относятся:

1)  выбор лучших/худших особей популяции;

2)  лучший уровень приспособленности в популяции;

3)  размер популяции;

4)  удаление повторяющихся особей.

Стратегия направленной эволюции реализована с помощью двух условий. Первое условие учитывает длину цепочки поколений, в которых лучший уровень приспособленности не меняется. Количество используемых генетических операторов увеличивается в зависимости от длины цепочки. То есть, чем длиннее цепочка, тем больше генетических операторов используется и тем более эти операторы изменяют популяцию.

На рисунке 1 представлена блок-схема разработанного алгоритма.

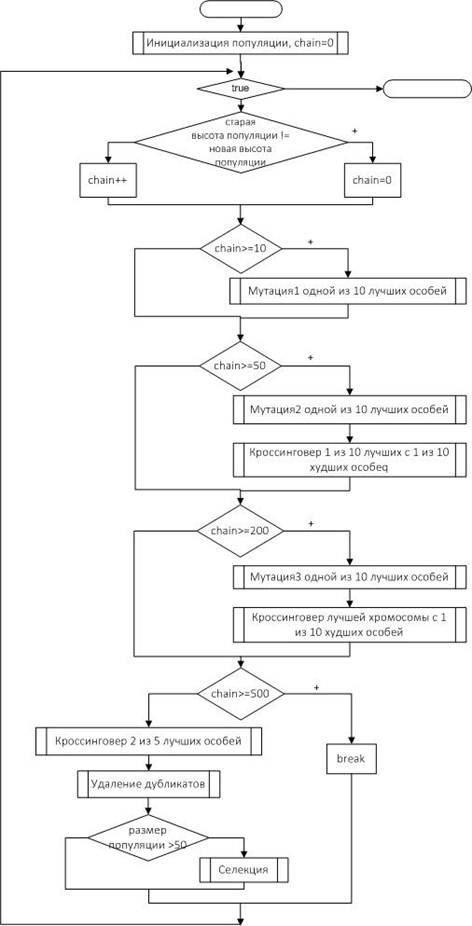
Рисунок 1. Блок-схема генетического алгоритма

Алгоритм реализован на языке C++. Проверка работоспособности и эффективности производилась на полных, взвешенных графах с разным количеством вершин: 5, 10, 20 и 100. С помощью жадного алгоритма найден минимальный вес гамильтонова цикла. Разумеется, это не будет лучшим решением, однако этого достаточно для сравнения результатов. На рисунке 2 представлен график, отражающий результаты сравнения работы генетического алгоритма и жадного.

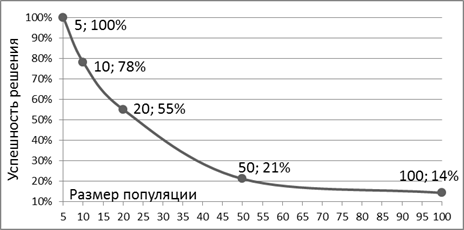
Рисунок 2. Зависимость успешности решения задачи от размера задачи

Полученные результаты показывают, что при увеличении размера задачи, успешность разработанного генетического алгоритма падает. Это можно исправить, изменяя настройки алгоритма, тонко подбирая параметры для того, чтобы получить оптимальный результат. Однако этих результатов достаточно для завершения исследования генетических алгоритмов.

Подводя итог, можно сказать, что методы решения задач с помощью генетических алгоритмов были в достаточной степени изучены. Также во время разработки был создан генетический алгоритм. Несмотря на то, что он оказался неэффективным, наработки по этому исследованию можно использовать в дальнейшем, чтобы улучшить результаты.