МАТРИЧНАЯ МОДЕЛЬ СРАВНЕНИЯ СТРОК ОДИНАКОВОЙ ДЛИНЫ С УДВОЕННЫМИ СИМВОЛАМИ
Секция: 3. Информационные технологии

XXXVI Студенческая международная заочная научно-практическая конференция «Молодежный научный форум: технические и математические науки»
МАТРИЧНАЯ МОДЕЛЬ СРАВНЕНИЯ СТРОК ОДИНАКОВОЙ ДЛИНЫ С УДВОЕННЫМИ СИМВОЛАМИ
В настоящее время информационные системы персональных данных характеризуются большим объемом фондов. Количество дополняемых и обновляемых записей в таких системах может достигать нескольких миллионов за один год. При этом, учитывая, что данные поступают из различных источников, не всегда можно гарантировать, что в персональных данных не содержатся ошибки. Например, данные могут поступать в информационную систему от десятков государственных учреждений, оказывающих различные услуги гражданам. На местах они заносятся операторами, и использование справочников в таком случае не всегда возможно, и даже при комбинированном подходе с использованием справочников остается определенный процент ошибок, попадающих в общую информационную систему. Как следствие, при создании поискового аппарата разработчики имеют дело с задачами, в которых необходимо оперировать нечеткими понятиями и знаниями. К таким задачам можно отнести, например, поиск с учетом различий в написании слов, дублирования данных и т.п.
Для решения перечисленных задач обычно используют алгоритмы нечеткого поиска. Существующие алгоритмы сравнивают строки между собой. Однако персональные данные представляют собой особую категорию строк, сравнение которых алгоритмами нечеткого поиска не всегда дает верный результат. Основными персональными данными являются фамилия, имя, отчество – основная триада персональных данных. Специфика этой категории заключается в том, что один из составных компонентов может отсутствовать, или же, наоборот, появиться дополнительный. Подобная ситуация характерна для большинства многонациональных государств, в частности, для России, где такие случаи далеко не редкость. Естественно, что количество ошибок становится больше, если вводятся персональные данные имеющие свои особенности в регионе, где таких особенностей нет.
Таким образом, актуальность настоящей работы определяется необходимостью разработки эффективного алгоритма нечеткого поиска, применяемого для сравнения персональных данных.
Ранее в процессе решения проблемы сопоставления строк с учетом наличия ошибок (не более двух) уже был создан матричный алгоритм, позволяющий устанавливать точность совпадения двух слов. Результаты работы были представлены на конференции «Катановские чтения 2016».
Разработанный алгоритм был успешно использован при установлении сходства различных строк. Однако при сравнении слов одинаковой длины, содержащих удвоенные символы, алгоритм выдавал неверные результаты сравнения.
В результате поиска решения возникшей проблемы на основе имеющейся теоретической базы была создана новая вариация алгоритма - матричная модель сравнения строк одинаковой длины с удвоенными символами, которая будет представлена в данной статье.
Теоретические основы алгоритма
Пусть в базе данных имеется строка-образец S длины N над некоторым алфавитом A. При этом S содержит хотя бы одну пару удвоенных символов, то есть существуют элементы строки, удовлетворяющие условию:
![]() .
.
Из строки S образуем строку C той же длины N с помощью возможных операций редактирования (замены, вставки, удаления символа, транспозиции), учитывая, что максимальное количество несовпадений этих строк не превышает двух элементов.
Перед тем, как начать построение матрицы сравнения [4, c.112], надо установить диапазон точного смещения.
Определение 1. Диапазон точного смещения это множество D элементов bij, в границах которых происходит смещение элементов вида bii относительно индекса j=![]() .
.
В данном случае (сравнение слов одинаковой длины с удвоенными символами) диапазон точного смещения имеет вид:
![]() .
.
Далее, построим бинарную матрицу B, элементы которой определяются сходством соответствующих символов двух строк и принадлежат множеству D, то есть:
![]() . (1)
. (1)
Введем следующее определение.
Определение 2. След диапазона точного смещения L – сумма всех возможных элементов bij, принадлежащих множеству D, т.е:
![]() .
.
Тогда справедлива следующая теорема.
Теорема. Два слова одинаковой длины с удвоенными символами совпадают с точностью двух несовпадений, если справедлива формула
![]() ; (2)
; (2)
где:
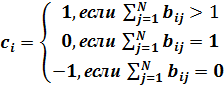 ; (3)
; (3)
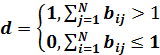 . (4)
. (4)
Таким образом, алгоритм сравнения строк преобразуется к следующему виду:
1. Построить матрицу B;
2. Найти ![]() ,
, ![]() ,
, ![]() ;
;
3. Определить справедливость равенства ![]() ;
;
4. На основании справедливости равенства установить сходство строк с точностью до двух несовпадений.
Для иллюстрации действия алгоритма выбран наиболее распространенный вариант сравнения: сопоставление строк, полученных в результате вставки произвольного и удаления удвоенного символа.
Пример. Установить сходство строк S=«ИННОКЕНТИЙ» и C=«ИНОКЕНСТИЙ», длины которых равны 10.
Решение.
Таблица 1.
Матрица сравнения строк S и C
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
|
И |
Н |
Н |
О |
К |
Е |
Н |
Т |
И |
Й |
|
1 |
И |
1 |
0 |
|
|
|
|
|
|
|
|
|
2 |
Н |
0 |
1 |
1 |
|
|
|
|
|
|
|
|
3 |
О |
|
0 |
0 |
1 |
|
|
|
|
|
|
|
4 |
К |
|
|
0 |
0 |
1 |
|
|
|
|
|
|
5 |
Е |
|
|
|
0 |
0 |
1 |
|
|
|
|
|
6 |
Н |
|
|
|
|
0 |
0 |
1 |
|
|
|
|
7 |
С |
|
|
|
|
|
0 |
0 |
0 |
|
|
|
8 |
Т |
|
|
|
|
|
|
0 |
1 |
0 |
|
|
9 |
И |
|
|
|
|
|
|
|
0 |
1 |
0 |
|
10 |
Й |
|
|
|
|
|
|
|
|
0 |
1 |
1. Запишем бинарную матрицу B (таблица 1).
2. Найдем элементы длины строк S и C (см. формулу 2).
3. ![]() .
.
4. Сумма элементов (![]() , (
, (![]() , тогда:
, тогда:
![]() (см. формулу 3),
(см. формулу 3),
5. ![]() , так как нет ни одного столбца, в котором сумма элементов превышает единицу (см. формулу 4).
, так как нет ни одного столбца, в котором сумма элементов превышает единицу (см. формулу 4).
6. ![]() .
.
7. Справедливость равенства (2) установлена, а значит, количество несовпадений строк S и C равно двум.
Заключение
В статье представлен матричный алгоритм сравнения строк одинаковой длины с удвоенными символами. Как было замечено ранее, данный алгоритм представляет лишь вариацию имеющейся математической модели сравнения слов.
Таким образом, была разработана целостная теоретическая основа возможного алгоритма нечеткого поиска. Вероятно, простота и быстродействие данного алгоритма окажутся его конкурентным преимуществом в случае работы с большими массивами данных. Результаты исследования могут быть использованы разработчиками БД в целях повышения эффективности проектирования. В частности, представленные разработки могут быть использованы специалистами в качестве основы для создания собственных алгоритмов нечеткого поиска.
Для дальнейшего исследования представляет интерес проведение экспериментального тестирования. В рамках данного тестирования необходимо провести сравнительный анализ эффективности предложенного алгоритма.





