Исследование ловчих сетей пауков на примере вида Singa Hamata

Аннотация. Многое в окружающем нас мире устроено не случайно, так, например, такие невероятные и сложные механизмы построения ловчих сетей заложены на некоем уровне у пауков, и успешно используются для жизни. Если понаблюдать за пауками, то на первый взгляд, они не вызовут восторга, но какие они плетут паутины! Как у них получаются столь красивые и совершенные сети? Попробуем разобраться, насколько сложна конструкция ловчих сетей.

Ключевые слова: конструкция ловчих сетей; логарифмическая спираль; спираль Архимеда, Самюэль Браун; парабола; анаморфоза.

Окружающий нас мир очень многообразен. Во все времена люди стремятся не только разгадать тайны природы, но и открыть для всех неизведанное, непонятное, скрытое от глаз обычного обывателя, а, самое главное, затем использовать в жизни. Ни для кого не секрет, что много научных изобретений сделано на основе открытий в области природы. Если понаблюдать за пауками, то на первый взгляд, они не вызовут восторга, но какие они плетут паутины! Как у них получаются столь красивые и совершенные сети? Попробуем разобраться, насколько сложна конструкция ловчих сетей.

Пауки – одни из древнейших обитателей нашей планеты, заселившие сушу более 200 миллионов лет назад. В природе насчитывается около 35 тысячи видов пауков. Но самая главная их отличительная особенность – способность производить паутинный шелк, непревзойденное по прочности натуральное волокно. Пауки используют паутину для самых разнообразных целей: для перемещения, охоты, построения жилища, коконов для яиц, размножения, но самая интересная – для построения ловчих сетей. Ловчие сети необходимы пауку для поимки добычи. В зависимости от постройки, сеть может обездвижить добычу, затруднить ее передвижение или просигнализировать о её появлении. Рассмотрим, как строится классическая колесовидная ловчая сеть. Для того чтобы её построить, обычно, первым делом паук выпускает довольно длинную прочную нить. Когда конец её цепляется за другую опору, то паук проползает по ней чтобы хорошо закрепить его. Иногда, чтобы укрепить паутину, паук проползает по ней еще несколько раз. Такая линия является своеобразным мостиком для паука и получила название подвесной нити. Затем он выпускает свободно свисающую нить и от ее середины начинает еще одну нить. Получается конструкция в виде буквы Y. Таким образом, строятся первые радиусы, а далее строится еще множество другие радиальных лучей. После того, как все радиусы построены, паук приступает к созданию вспомогательной спирали, которая дальше ему поможет при построении ловчей сети. Причем весь основной каркас и вспомогательная спираль строятся из неклейкой нити, а вот ловчая часть делается из более прочной нити, покрытой клейким веществом. Удивительно то, что вспомогательная спираль и ловчая имеют ярко выраженные формы спирали, отличающиеся по своей структуре. Вспомогательная спираль имеет относительно малое число витков, и расстояние между ними с каждым витком увеличивается. Происходит это потому, что, прокладывая ее, паук движется под одинаковым углом к радиусам. Форма получившейся такой линии очень близка к логарифмической спирали (рис.1). Липкая ловчая спираль строится немного по другому принципу. Паук, начиная от края, двигается к центру, сохраняя одинаковое расстояние между витками. Таким образом, данный тип спирали более похож на спираль Архимеда (рис.2). Выходит, когда паук заканчивает длительное построение своей ловчей сети, получается необыкновенная по структуре паутина.

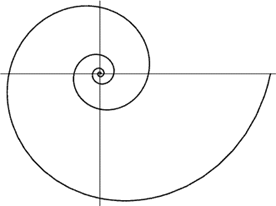
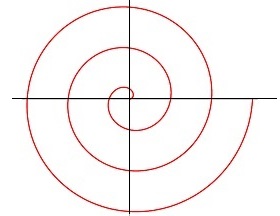
Рисунок 1. Логарифмическая           Рисунок 2. Спираль 

Конструкция сети паутины прочно укрепилась при строительстве подвесных мостов. Изобрел их английский инженер Самюэль Браун. Когда он решал задачу сооружения перехода без опор через реки и обрывы, обратил внимание на нить паутины, переброшенную от одного дерева, на другое. Ученый отметил, что при сильном ветре паутина не рвется, так как обладает высокой прочностью. Тогда у Самюэля Брауна и появилась идея, которая получила инженерное воплощение и дала множество вантовых мостов.

В процессе выбора конкретного объекта исследования были изучены фотографии разнообразных форм ловчих сетей. В процессе работы отмечена одна довольно интересная схема, отличавшаяся от привычных сетей своим видом. Схема сделана по настоящей ловчей сети паука вида Singa Hamata (рис. 3), который относится к роду пауков Singa. Синга–мелкие (до ~5 мм), повсеместно встречающиеся пауки - кругопряды. Этот вид пауков плетёт вертикальные круглые сети близ поверхности почвы, прикрепляя их к стеблям или низко висящим ветвям. Обратим внимание на то, что их сеть имеет ярко выраженную ассиметрию, то есть нижняя часть паутины вытянута вниз. Но сама паутина выглядит красиво и имеет довольно плотную компактную структуру. Что удивляет в данной паутине? Это то, что паук не сидит непосредственно на паутине и выжидает добычу, не наблюдает за паутиной сидя рядом, он поступает наиболее хитрым образом: от паутины пускает сигнальную нить за собой и уходит в убежище. Сидя на листке, ждет, когда «зазвонит» нить и идет за своей добычей. Привлекает вид паутины, точнее ее нижняя и верхняя части. Если их разделить и присмотреться, то можно заметить сходство нижней части с параболой, а верхней с эллипсом. Попробуем проверить так ли это.

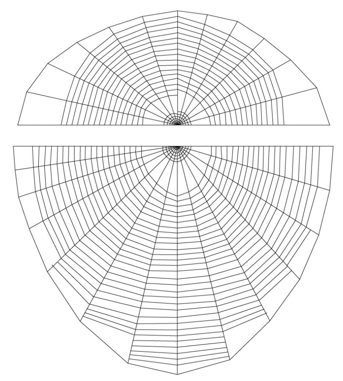
Рисунок 3. Схема ловчей сети Singa Hamata

Добавим оси и возьмем контрольные точки для дальнейшего построения графика. Возьмем уравнение   , проинтегрировав его получаем . Теперь, когда знаем анаморфозу, строим график (рис. 4).

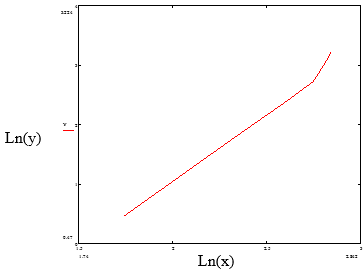
Рисунок 4. График анаморфозы для уравнения параболы

Данные практически идеально спрямились за исключением последней точки. Можно утверждать, что нижняя часть паутины действительно является моделью параболы.

Проделаем аналогичную работу и для верхней части.

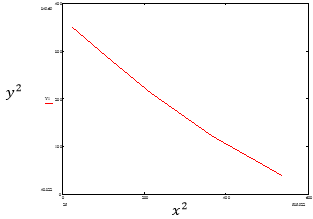
Рисунок 5. График анаморфозы для уравнения эллипса

Из графика видно, что данные практически полностью спрямились. Это означает, что верхняя часть паутины имеет модель эллипса.

В процессе измерений стал заметен ещё один интересный факт. Когда измеряем значения, то держим верхнюю и нижнюю части схемы в обычном положении, как показано ниже (рис. 6).

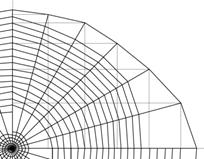
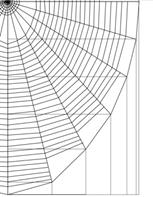
Рисунок 6. Схема ловчей сети Singa Hamata (слева – верхняя часть сети, справа – нижняя)

Однако если верхнюю часть схемы мы развернем, то увидим, что части становятся очень похожими (практически идентичными).

Рисунок 7. Развернутая на 90 градусов верхняя часть схемы ловчей сети

Возьмем схему ловчей сети, повернем его против часовой стрелки на 90 градусов и измерим общую длину главной оси. Получаем число, равное 20.2 см. Возьмем за 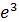 число 20.2. Далее, с помощью расчетов получаем, что за «единицу» берем число, равное 1.0057. Построим шкалу с основными значениями (рис. 8). 

Рисунок 8. Шкала с основными значениями для полной схемы

Наложим эти значения на паутину, отсчитывая справа налево, и получим довольно интересный результат. Значение 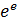 точно попадает в начало свободной зоны, а если сместимся еще на период 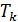, то увидим окончание свободный зоны и начало ловчей части паутины. Тем самым видно, что в значении 10.2 начинается глобальное изменение структуры и наблюдаем свободную зону ловчей сети. Когда доходим до значения 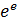, спустя еще один период 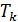, отчетливо видно, что заканчивается свободная зона, и вид паутины принимает новую структуру. Далее возьмем за основу (e^3) центр паутины, который разделяет верхнюю и нижнюю части. Длины соответственно равны 6.8 см и 13.4 см. Построим еще одну шкалу со значениями, на которой сверху нанесены данные верхней части паутины, снизу соответственно для нижней части и получим следующий результат (рис. 9).

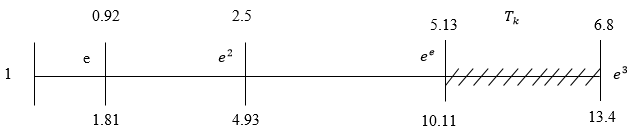
Рисунок 9. Шкала для верхней и нижней частей паутины

Нанесем данные значения на паутину и увидим достаточно интересную картину. Моменты, когда кардинально меняется структура, совпадают с нанесенными ранее данными и приходятся на начало свободной зоны ловчей сети. Измерим общую длину свободной зоны и получим значение 5 см. Возьмем его за e^3, вычислим значение в e^2, которое оказалось равным 1.84 см. После того, как отмерим это расстояние, обнаружим, что оно совпадает с центром паутины. Построим градусную шкалу, подобную выше используемой. Максимальным градусом примем число 360 (рис. 10). 

Рисунок 10. Градусная шкала

Взяв схему в ее начальном виде, прикладываем транспортир и идем до 270 градусов. Теперь смотрим, что же происходит в этом 90-градусном сегменте. Наблюдаем следующее: смена структуры. Ближе к концу учащение секторов, и, как следствие, уменьшение угла сектора. Также сложно не заметить и то, что теперь в 90-градусном не 6 секторов, как было в 3-х предыдущих, а 7. Еще одно наблюдение: количество секторов (ровно, как и радиусов всей паутины) равно 25. Известно, что 25 это квадрат числа 5. Присмотревшись к центральной зоне исследуемой ловчей сети, видим количество витков спирали равное 5.

В представленной работе проведено исследование строения ловчих сетей паука в целом и Singa Hamata в частности. В ходе исследования выявлены интересные факты строения ловчих сетей. При анализе схемы сети данного вида пауков, изначально было отмечено, что она имеет сильную асимметрию снизу, но в процессе работы она оказалась недостаточно ассиметричной. Исследование убеждает в том, что колесовидные ловчие сети являются классическими резонансными структурами и приводит к выводу, что многое в окружающем мире устроено не случайно.