Расчет отвода газа в боковых газоотводных устройствах
Конференция: XLII Международная научно-практическая конференция «Научный форум: инновационная наука»
Секция: Технические науки

XLII Международная научно-практическая конференция «Научный форум: инновационная наука»
Расчет отвода газа в боковых газоотводных устройствах
CALCULATION OF GAS OUTLET IN SIDE GAS VENTING DEVICES
Stanislav Pototsky
Major, Adjunct of the Branch of VA MTO, Russia, Penza
Sergey Kukanov
Lieutenant Colonel, Branch of VA MTO (Penza), Russia, Penza
Alexey Gromov
Sergeant, squad leader of the Branch of the VA MTO (Penza), Russia, Penza
Аннотация. В статье рассмотрен ряд газоотводных устройств. Проведен анализ порядка расчета боковых газоотводных устройств различных научных школ. Выведены ряд общих зависимостей, в том числе зависимость давления и скорости отвода пороховых газов от угла и отвода пороховых газов и площади газоотводного отверстия.
Abstract. The article discusses a number of gas venting devices. The analysis of the procedure for calculating the lateral gas venting devices of various scientific schools. A number of general dependencies have been derived, including the dependence of the pressure and rate of removal of powder gases on the angle and removal of powder gases and the area of the gas outlet.
Ключевые слова: расчет, критерии, уравнение, газоотводный двигатель.
Keywords: calculation, criteria, equation, gas engine.
Расчет отвода порохового газа из канала ствола или полости дульного устройства через боковые отверстия сводится к решению задачи истечения газа, движущегося в канале, через отверстие в его стенке. В теоретической гидромеханике решение этой задачи изучено недостаточно. Опытами установлено, что на сужение струи и расход газа определяющее влияние оказывают скорость газового потока в канале в месте расположения отверстия, угол наклона отверстия к оси канала, а также поперечные размеры отверстия, канала и толщина стенок. Однако имеющиеся эмпирические зависимости для коэффициента расхода при отводе порохового газа из канала ствола через боковое отверстие не согласуются между собой при одинаковых значениях скорости газа в канале и угла наклона отверстия показано на рисунке 4.
Исходя из общего анализа качественной картины бокового истечения, явление бокового отвода в зависимости от относительной толщины стенки канала можно подразделить на два случая:
- истечение через отверстие в «тонкой» стенке, т. е. через боковое отверстие с такой геометрией, при которой отсоединившаяся струя не соприкасается со стенкой, кроме входных кромок, и направление ее скорости движения не совпадает с осью отверстия показано на схеме на рисунке 1;
- истечение через отверстие в «толстой» стенке, т. е. через боковое отверстие с такой геометрией, при которой отсоединившаяся струя после взаимодействия со стенкой принимает движение, направление скорости которого совпадает с направлением оси отверстия показано на схеме на рисунке 2.
Рассмотрим приближенный способ расчета коэффициентов сужения струи для этих случаев истечения при противодавлении, близком нулю, полагая, течение газа плоским, установившимся и теплоизолированным, а поперечное сечение канала бесконечно большим по сравнению с размером бокового отверстия.
Истечение через отверстие в «тонкой» стенке. Физическая картина отвода газа через малое отверстие в «тонкой» стенке представляется следующей. Часть потока газа, движущегося вдоль стенки канала, при подходе к боковому отверстию под действием статического давления изменяет направление своего движения и вытекает через боковое отверстие. При этом составляющая скорости газа в направлении основного потока в канале остается неизменной при переходе частиц газа через кромки отверстия. Во всех точках кривой, ортогональной линиям тока и проходящей через входную кромку, относительная скорость газа считается одинаковой, а сама кривая аппроксимируется дугой окружности показано на схеме на рисунке 1 с центральным углом 2θ0, определяемым из соотношения
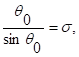
![]() (1)
(1)

Рисунок 1. Схема истечения газа через боковое отверстие в «тонкой» стенке
Переносное движение вызывает снос относительного движения. Будем полагать, что с увеличением переносной скорости V∞ радиус дуги, ортогональной линиям тока, уменьшается и сама дуга смещается в сторону противоположную переносному движению. В противном случае под влиянием переносного движения частицы газа, притекающие к дуге CDM в относительном движении, не будут выходить из отверстия. Величина отношения хорды дуги СМ к поперечному размеру отверстия СЕ зависит от соотношения между переносной и относительной скоростями и определяется из геометрических соображений выражением
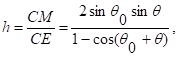 (2)
(2)
Здесь v - относительная скорость, v∞ - переносная скорость основного потока. Используя эту зависимость и применяя к участку струи ABCDE уравнения сохранения массы, количества движения и энергии, будем иметь для случая истечения с максимальным расходом систему уравнений:
 (3)
(3)
где εm= AB/СЕ; а = kр/ρ - скорость звука. Здесь индексами 1 и 2 отмечены параметры газа в суженном сечении АВ и на дуге CDM. Индексом ∞ обозначены параметры газового потока в бесконечно широком канале перед отверстием.
С учетом этих соотношений и введения газодинамических функций решение системы уравнений (3) позволяет определить наибольшее значение коэффициента сужения газовой струи при боковом истечении через малое отверстие в «тонкой» стенке и угол наклона отсоединяемой струи
 (4)
(4)
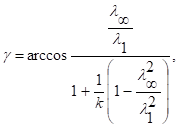 (5)
(5)
Коэффициент σ при θ = 90° равен
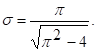 (6)
(6)
В теории газовых струй не получены числовые значения коэффициента сужения для рассматриваемого случая истечения. Система уравнений (3) при ρ1 = ρ2 = ρ∞ и к → ∞ для несжимаемой жидкости имеет следующее решение
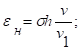 (7)
(7)
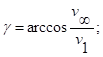 (8)
(8)
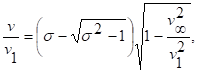 (9)
(9)
где σ определяется соотношением (6), a h находится из зависимости (2) и соотношения (1). Выражение (8) тождественно точному решению.
Определим теперь коэффициент сужения при боковом истечении газа через отверстие в «толстой» стенке. Будем полагать, что в этом случае истечения при λ∞ < 1 описанная выше физическая картина движения газа на входе в отверстие сохраняется. Расчетная схема изображена на рисунке 2.

Рисунок 2. Схема истечения газа через боковое отверстие в «толстой» стенке
В принятых выше обозначениях система уравнений сохранения массы, количества движения и энергии имеет следующий вид:
 (10)
(10)
где φ - угол наклона оси отверстия относительно вектора скорости потока газа в канале. Здесь полагаем, что после ударного взаимодействия отсоединяемой струи со стенкой в сечении АВ наибольшего сужения струи устанавливаются критические условия ![]() . Тогда из системы уравнений (10) с применением газодинамической функции q(λ) можно определить наибольшее значение коэффициента сужения газовой струи при истечении через отверстие в «толстой» стенке в виде следующей зависимости
. Тогда из системы уравнений (10) с применением газодинамической функции q(λ) можно определить наибольшее значение коэффициента сужения газовой струи при истечении через отверстие в «толстой» стенке в виде следующей зависимости
 (11)
(11)
Здесь значения σ и h определяются по выражениям (1), (2) и (6). В частном случае, когда газ в канале неподвижен (λ∞ = 0), зависимость (11) принимает вид
![]() (12)
(12)
где  и определяет наибольшее значение коэффициента сужения при истечении газа через наклонное отверстие при прямоточном истечении показано на рисунке 3.
и определяет наибольшее значение коэффициента сужения при истечении газа через наклонное отверстие при прямоточном истечении показано на рисунке 3.
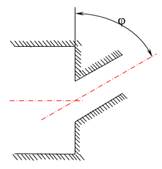
Рисунок 3. Схема входного участка с наклонным отверстием
Полученная зависимость (12) позволяет определить коэффициент расхода порохового газа при критическом режиме истечения через боковое малое отверстие в стенке ствола по соотношению
 (13)
(13)
где 0,97 – коэффициент скорости, а отношение в скобках представляет величину относительного уменьшения коэффициента сужения струи, равную 0,83 согласно графику, на рисунке 1 для θ = 90° при увеличении противодавления от нуля до критического. На рисунке 4 приведено сопоставление результатов вычислений коэффициента μкр по расчетным зависимостям (12) и (13). с известными эмпирическими формулами, полученными в разные годы в диссертационных работах: Г. А. Жирных (1958 г.), А. П. Пудовеева (1961 г.), В.И. Кулагина (1969 г.).

Рисунок 4. Сопоставление коэффициентов расхода при боковом истечении, вычисленных по расчетным зависимостям, с эмпирическими формулами:
1 - формула Г.А. Жирных; 2 - формула А.П. Пудовеева;
3 - формула В.И. Кулагина; 4 - зависимости (12) и (13)
Зависимости (4) и (12), определяющие коэффициент сужения газовой струи, получены для бокового отвода газа из канала бесконечной ширины по сравнению с размером бокового отверстия. Однако при решении практических задач, как правило, приходится рассчитывать боковой отвод газа из канала конечной ширины показано рисунке 5, когда поперечное сечение бокового отверстия соизмеримо или больше поперечного сечения канала.

Рисунок 5. Схемы бокового отвода газа из канала конечной ширины через отверстия в «тонкой» и «толстой» стенке
С целью создания инженерного метода расчета бокового отвода газа из канала конечной ширины было проведено численное интегрирование дифференциальных уравнений, описывающих изменения плотности, массы и количества движения одномерного потока, движущегося в канале постоянного сечения с непрерывным оттоком массы через элементарные участки боковой поверхности с коэффициентами сужения отводимых элементарных струй, определяемыми по зависимостям (4) и (12) для отверстий в «тонкой» и «толстой» стенке. В результате были вычислены при к = 1,25 специальные газодинамические функции Ф(λ), Ф (φ; λ), Ω(λ) и i(λ).
Из анализа боковой отвод газа из потока, движущегося в канале, через отверстия в «тонкой» или «толстой» стенках приводит к замедлению дозвукового потока и к дальнейшему ускорению сверхзвукового потока, как в расширяющемся насадке, также следует, что на величину коэффициента сужения определяющее влияние оказывает угол отвода газа.


