Усовершенствованный алгоритм Дейкстры как основа разработки программного обеспечения для поиска оптимального маршрута на дорогах Республики Казахстан

Аннотация. В статье рассматривается алгоритм Дейкстра, как основа для дальнейшего усовершенствования и разработки программного средства. Выбор задачи кратчайшего пути является одним из классические проблемы теории графов. Одним из распространенных алгоритмов решения проблемы кратчайшего пути является алгоритм Дейкстры. В данной работе алгоритм Дейкстры был преобразован для работы с реальными данными, применяемыми на территории Республики Казахстан.

Ключевые слова: кратчайший путь; алгоритм Дейкстры; граф; проблемы нахождения кратчайшего пути; OSPF.

В настоящее время мобильные устройства становятся все более распространенными и все чаще используются для многих целей. Меньше потребителей используют мобильные устройства только для одной цели. Современные мобильные устройства поддерживают растущий спектр дополнительных приложений - запись и воспроизведение аудио, видео и изображений, подключение к социальным сетям, поиск и получение данных из Интернета и получение информации GPS [1]. В то же время современные информационные и коммуникационные технологии дают возможность использовать мобильные устройства для их дальнейшего обучения. Использование географических информационных систем значительно возросло с восьмидесятых и девяностых годов. В качестве одного из самых требовательных приложений можно упомянуть поиск кратчайших путей. Несколько исследований о поиске кратчайшего пути показывают целесообразность использования графов для этой цели. Алгоритм Дейкстры является одним из классических алгоритмов поиска кратчайшего пути.

Кратчайший путь — фундаментальная проблема теории графов. Это также может быть одной из основных проблем в сетевом анализе. Проблема кратчайшего пути — это проблема поиска кратчайшего пути или маршрута от начальной точки до конечного пункта назначения. Как правило, чтобы представить проблему кратчайшего пути, мы используем графы. Граф — это математический абстрактный объект, который содержит наборы вершин и ребер. Ребра соединяют пары вершин. Можно следовать по краям графа, перемещаясь из одной вершины в другую [2]. В зависимости от того, можно ли следовать по краям в обе стороны или только в одну сторону, определяется, является ли граф ориентированным или неориентированным. Кроме того, длины ребер часто называют весами, и веса обычно используются для вычисления кратчайшего пути от одной точки к другой точке. В реальном мире можно применить теорию графов к различным типам сценариев. Например, чтобы представить карту, мы можем использовать график, где вершины представляют города, а ребра представляют маршруты, соединяющие города. Если маршруты односторонние, тогда график будет направлен; в противном случае оно будет ненаправленным.

Кратчайший путь является одной из наиболее важных проблем оптимизации в теории графов, и он был горячей темой исследований в области компьютерной науки, организации трафика, геоинформационных систем (ГИС), исследования операций и т. д. Для того, чтобы четко показать свою роль, в этой статье будет разработан алгоритм Дейкстры на примере выбора оптимального маршрута транспортного средства на территории Республики Казахстан. Этот алгоритм является одним из самых популярных и совершенных в задачах нахождения кратчайшего пути из одного источника, и в настоящее время он также признан лучшим алгоритмом для поиска кратчайшего пути в неотрицательных весах, и когда все веса равны нулю [3]. Но в этом методе все еще есть некоторые недостатки, и если не устранить эти недостатки и использовать метод напрямую, это приведет к ненужным потерям. Разработанный алгоритм будет применен в программном обеспечении, который находит кратчайший путь между двумя пунктами республиканского и международного значения на территории страны, при этом алгоритм будет усовершенствован, учитывая нюансы, появляющиеся в ходе научной работы.

Выделяются следующие проблемы кратчайшего пути из одного источника (Рисунок 1):

• Проблема нахождения кратчайших путей из источника вершины v ко всем остальным вершинам графа.
• Взвешенный граф G = (E, V)
• Исходная вершина s ∈ V для всех вершин v ∈ V

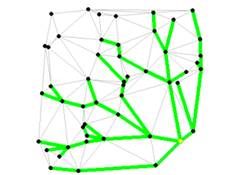
Рисунок 1. Демонстрация работы алгоритма Дейкстры

Решением проблемы кратчайшего пути из одного источника в теории графов является:

• Как ориентированные, так и неориентированные графы
• Все ребра должны иметь неотрицательные веса
• График должен быть связным

Идея алгоритма Дейкстры проста. Дейкстра разделяет все узлы на два разных набора: неустановленные и установленные. Первоначально все узлы находятся в неустановленных наборах, например, они должны быть еще оценены. Узел перемещается в установленный набор, если был найден кратчайший путь от источника к этому узлу [4].

Алгоритм Дейкстры уникален по многим причинам, которые мы скоро увидим, когда начнем понимать, как он работает. Но то, что всегда было небольшим сюрпризом, это тот факт, что этот алгоритм используется не только для поиска кратчайшего пути между двумя конкретными узлами в структуре данных графа. Алгоритм Дейкстры можно использовать для определения кратчайшего пути от одного узла в графе к каждому другому узлу в той же структуре данных графа, при условии, что узлы достижимы от начального узла. Наиболее распространенный пример алгоритма Дейкстры в дикой природе- это проблемы с поиском пути, такие как определение направлений или поиск маршрута в GoogleMaps.

Однако, чтобы найти путь через GoogleMaps, реализация алгоритма Дейкстры должна быть еще более разумной, чем та, которую мы создал. Версия алгоритма Дейкстры, которая реализована здесь, по-прежнему не так умна, как большинство форм, используемых на практическом уровне. Представьте себе не только взвешенный график, но и необходимость вычислять такие вещи, как трафик, дорожные условия, перекрытия дорог и строительство.

Общая стратегия алгоритма заключается в следующем. Учитывая начальный узел, нужно вычислить расстояние каждого из его соединений (называемых ребрами). Какое бы соединение ни было кратчайшим, необходимо следить за ним, сохраняя счет общего расстояния, пройденного по этому конкретному пути. Следует повторять, пока не дойдет до последнего интересующего узла (Рисунок 2).

Итак, если мы заинтересованы в переходе от A к E, начнем со всех соединений A, которыми являются B и C. Расстояние до C равно двум, а расстояние до B равно четырем. Два меньше четырех, поэтому мы переходим к узлу С. Теперь мы обновляем наш путь как A -> C, и наша общая сумма равна 2.

Сейчас мы рассмотрим все наши возможные варианты. Переход от А к В еще четыре. Переход от С к D - четыре, а от С до F - шесть (нужно помнить, что добавляется расстояние нового соединения к итогу - то есть расстояние от А).

Поскольку шесть больше четырех, мы знаем, что C на F отсутствует. Теперь выбираем случайным образом между A -> B и C -> D. Предположим, что выбирается C -> D. Необходимо обновить наш путь и общий путь: A -> C -> D итог: 4.

Теперь рассмотрим все варианты. A -> B - все еще четыре, D -> F - пять, а D -> E - семь. Четверка самая низкая, поэтому мы выбрали этот маршрут. На данный момент, общие шаги алгоритма имеют смысл.

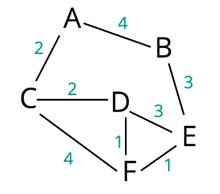
Рисунок 2. Алгоритм Дейкстры

Для моделирования в коде понадобятся три основные структуры данных:

• Таблица хеширования расстояния: понадобится таблица, которая отображает общее расстояние каждого узла от начального узла. Ключом будет узел, а значением будет его промежуточный итог.
• Очередь приоритетов: когда сравниваются все возможные маршруты, которые можно выбрать, очередь приоритетов будет покрывать наименьший возможный маршрут. Таким образом, не нужно каждый раз сканировать массив, который является самым маленьким.
• Хэш-таблица маршрутов: нужен способ отслеживать текущий путь, который строится. Ключом будет текущий узел, в котором мы находимся, а его значением будет узел, с которого он пришел.

Первоначально расстояние каждого узла до источника установлено на очень высокое значение, т.е. стремится к бесконечности, как продемонстрировано в последующем псевдокоде.

Сначала только источник находится в наборе unsettledNodes (не посещённые, неустановленные узлы). Алгоритм работают до тех пор, пока неустановленные узлы не станут пустыми. В каждой итерации выбирается узел с наименьшим расстоянием от источника из неустановленных узлов [5]. Он считывает все ребра, исходящие из источника, и оценивает для каждого узла назначения, по ребрам, которые еще не установлены если известное расстояние от источника до этого узла может быть уменьшено при использовании выбранного ребра. Если это можно сделать, то расстояние обновляется, и узел добавляется к узлам, которые нуждаются в оценке.

В псевдокоде алгоритм может быть описан следующим образом. Необходимо обратить внимание, что Дейкстра также определяет пре-преемника каждого узла на пути к источнику, но для упрощенного вида псевдокода, этот момент пропускается:

dist [s]←0  //расстояние до вершины источника равно нулю

for all v ∈ V-{s}

         do dist [v] ←∞  //предположение о том, что расстояние стремятся к бесконечности

S←  ∅//S, набор посещенных вершин изначально пуст

Q←V  //Q, очередь изначально содержит все вершины

while Q  ≠∅ //до тех пор, пока очередь не пуста

do u←mindistance (Q,dist)  //выбирается элемент Q с минимальным расстоянием

S←S ∪ {u}  //добавляется в список посещенные вершины

for all v ∈ neighbours [u]

         do if dist [v] > dist [u] + w (u,v)  //если найден новый кратчайший путь

                   then d [v] ← d [u] + w (u,v)  //добавляется новое значение в кратчайший путь

return dist

Системы дорожной информации используют алгоритм Дейкстры для отслеживания источника и пункты назначения из данного конкретного источника и пункта назначения.

OSPF (англ. Open Shortest Path First) — протокол динамической маршрутизации, основанный на технологии отслеживания состояния канала (link-state technology) и использующий для нахождения кратчайшего пути алгоритм Дейкстры. Он использует состояние ссылки в отдельные области, которые составляют иерархию [6].

Если вы когда-либо пытались найти расстояние или путь из одной точки / местоположения в другую точку / пункт назначения, скажем, из одного города в другой или из вашего местоположения до ближайшей заправочной станции, очень вероятно, что вы столкнулись с проблемой кратчайшим пути. В математике это поиск кратчайшего пути между двумя точками на графике, для которого весьма вероятно применение алгоритма Дейкстры [7].

Другим примером может быть то, что отдел пожарных хочет разработать систему, которая находит кратчайшее расстояние между ближайшим отделом пожарных и сжигаемым домом, чтобы избежать дополнительной задержки. Или логистические компании хотят разработать систему, которая находит кратчайшее расстояние между складом и пунктами назначения, чтобы избежать лишних затрат и времени. Для разработки таких систем алгоритм Дейкстры очень применим. Лучший маршрут проезда выбирается в основном из следующих аспектов: минимальная стоимость, кратчайшее расстояние и наибольшее количество придорожных сервисов. И они могут быть рассчитаны с помощью алгоритма Дейкстры. Фактически, алгоритм Дейкстры обеспечивает кратчайший путь от заданной точки к любой точке. Поэтому первым шагом является поиск всех участков, через которые проходит транспорт, между отправлением и пунктом назначения, и эти участки рассматриваются как фиксированная точка.

Во-вторых, нужно измерить пробег, который транспорт проезжает через два соседних участка, а пробег - это вес. Тогда самый короткий путь, который также является самым коротким маршрутом, может быть рассчитан с помощью алгоритма Дейкстры.

Проблема нахождения кратчайшего пути в графе является одной из проблем оптимизации. Граф, используемый при поиске кратчайшего пути, представляет собой взвешенный граф, сторонам которого присвоено значение или вес [8]. Веса на стороне графика могут указывать расстояние между городами, сроки доставки сообщений, стоимость разработки и так далее. Предположение, которое мы используем здесь, состоит в том, что все веса положительны [9]. Самое короткое имеет разное значение в зависимости от типичной проблемы, которую необходимо решить. Тем не менее, в общем случае самое короткое означает минимизацию весовых коэффициентов на диаграмме. В этой статье было проведено тематическое исследование ориентированного графа с различным числом узлов, чтобы проверить правильность предложенного алгоритма. Тот же пример был применен к оригинальному алгоритму Дейкстры с приоритетной очередью, реализованной в виде мини-кучи. Сравнение результатов показало, что предложенный алгоритм является едва ли не лучшим. Хотя в предложенном алгоритме было использовано больше структур данных, расширенное хранилище доступно для всех текущих устройств, даже для самых маленьких. Мы утверждаем, что хранилища данных не может стать проблемой, если производительность данного алгоритма высокая и успешна. Наблюдалось, что время поиска исходного алгоритма почти такое же, как и время предлагаемого алгоритма, если требуемый путь не является неявным путем в решении. Что касается результатов, время выполнения зависит от типа используемой структуры данных, а также от скорости процессора. Хотя результаты дают хорошее среднее время поиска в пути решения, мы понимаем, что чем больше число узлов, тем больше времени уходит на поиск пути. Это может работать в большом хранилище узлов, особенно в огромной дорожной сети.

Большинство доступных алгоритмов предполагают природу простого поиска пути в пути решения. Структура данных играет основную роль во всех процедурах и операциях. Мы осознаем этот момент, когда начинаем предлагать нашу идею по улучшению имеющегося алгоритма Дейкстры. Согласно результатам, улучшение предложенного алгоритма достигается с учетом направленного графа. Предложенный алгоритм применяется к реальной карте сетевой дороги, для демонстрации производительности и повышения достоверности с реальной точки зрения.