Адаптивная фильтрация сложных сигналов на фоне сосредоточенной по частоте помехи

Adaptive filtering of complex signals on a background focused frequency interference

Chernova Inna

Graduate student, Immanuel Kant Baltic Federal University, Russia, Kaliningrad

Аннотация. В статье представлен метод фильтрации сигналов, основанный на применении теории оптимального приема, позволяющий отфильтровывать как ортогональную, так и неортогональную часть помехи.

Abstract. The article presents the signal filtering method based on the application of the theory of optimal reception, enabling filtering both orthogonal and non-orthogonal part interference.

Ключевые слова: оптимальный прием; фильтрация; сложный сигнал; метод максимального правдоподобия.

Keywords: optimal reception; filtering; composite signal; the method of maximum likehood.

Существующие в настоящее время фильтры исключают только ортогональную к сигналу составляющую помехи. Метод максимального правдоподобия позволяет реализовать фильтры нового типа, способные решать задачу фильтрации как в области ортогональности помехи и сигнала, так и в области их неортогональности.

Рассмотрим более подробно технологию фильтрации сложного сигнала на фоне сосредоточенной по частоте помехи фильтром максимального правдоподобия. Пусть принятое сообщение имеет следующий вид:

,

где ,  – комплексные амплитуды сигнала и помехи,  – модулирующая функция,  – время приема сигнала, ,  – круговые частоты сигнала и помехи,  – аддитивный шум с нормальным законом распределения, дисперсией , средним значением равным нулю и интервалом корреляции .

Оптимальный алгоритм обработки при решении задачи оценки параметров сигнала определяется уравнениями правдоподобия[1,3].Логарифм функции правдоподобия при малом интервале корреляции  будет определяться выражением:

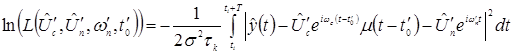,                                                (1)

где– время начала обработки.

Дифференцируя выражение (1) по амплитудам, и приравнивая дифференциалы к нулю, получим систему уравнений, решая которую найдем значенияи :

                                                                                                (2)

,

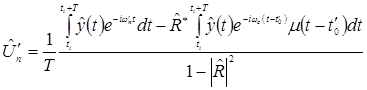где– коэффициент корреляции:

                                                                                         (3)

Таким образомможно оценить параметры помехи и скомпенсировать ее. Так для момента времени  значение сигнала на выходе фильтра будет определяться выражением:

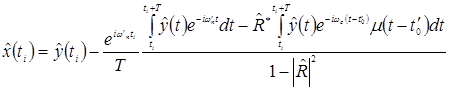                                                                      (4)

Однако в условиях априорной неопределенности указанных параметров необходимо получить их оценки. Для этого используется функционал правдоподобия, определяемый следующим выражением:

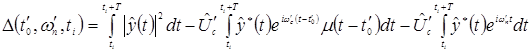                                                              (5)

Оценки времени приема сигнала и частоты помехи осуществляются путем нахождения значений и, минимизирующих функционал (5).

Блок фильтрации работает согласно уравнению (4) и производит компенсацию помехипри параметрах, определяемых адаптивной частью фильтра, что отличает его от классического винеровского адаптивного фильтра.

Представленный алгоритм адаптивной фильтрации был проверен с помощью модельных исследований, проведенных в среде MATLAB.Ниже приведенрезультат фильтрации сложного сигнала на основе 16-ти позиционной М-последовательности на фоне сосредоточенной по частоте помехи фильтром максимального правдоподобия.

Параметры сигнала: , , ,длительность сложного сигнала, параметры помехи: , ,. Принятое сообщениепредставлено на рисунке 1.

Рисунок 1 – Принятое сообщение

В результате применения фильтра максимального правдоподобия получаем сигнал, очищенный от помехи (рисунок 2).

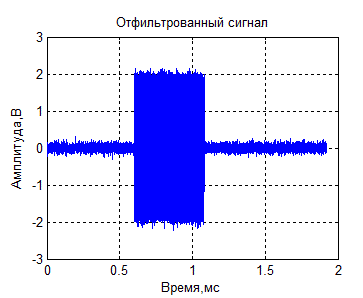
Рисунок 2 – Восстановленное сообщение

Параметры восстановленного сигнала:, ,  (, ). Таким образом, адаптивная фильтрация с оценкой параметров по методу максимального правдоподобия позволяет полностью избавиться от помехи.

Граничные возможности предложенного метода представлены на рисунке 3.

Рисунок 3 – Граничные возможности метода максимального правдоподобия

Результаты проведенных модельных исследований подтверждают основные положения теории.

Разработанная технология фильтрации позволяет исключить как ортогональную составляющую помехи, так и неортогональную. Диапазон изменения коэффициента взаимной корреляции между сигналом и помехой может изменяться в пределах от 0 до 0.9.