Совершенствование системы терморегулирования космических аппаратов
Конференция: I Международная заочная научно-практическая конференция «Научный форум: технические и физико-математические науки»
Секция: Авиационная и ракетнокосмическая техника

I Международная заочная научно-практическая конференция «Научный форум: технические и физико-математические науки»
Совершенствование системы терморегулирования космических аппаратов
Improvement of the thermal control system of space crafts
Sakhanov Kanat
Candidate of Engineering Sciences, Eurasian National university named after L.N. Gumilev, Kazakhstan, Astana
Kadyrov Medet
Undergraduate, Eurasian National university named after L.N. Gumilev, Kazakhstan, Astana
Аннотация: Основными показателями качества космических аппаратов (КА) является их надежность и срок активного существования (САС) на орбите, и существенную роль в этом играет температурный режим внутри объема КА, где находятся приборы. Одна из позиций их стабильной работы заключается в создании определенного теплового режима в объеме конструкции, для чего служит система терморегулирования, при которой тепловой режим обеспечивается с помощью вентилятора, включающегося от термореле при заданной температуре.
Abstract: The main indicators of the quality of space vehicles (SV) are their reliability and lifetime (LT) in the orbit, and a significant role in this plays a temperature mode inside of SV, where are the devices. And one of their stable work is to create a specific thermal regime in the volume of construction, what is the thermal control system in which the heat mode is provided with fan provided by thermal relay at a given temperature.
Ключевые слова: космические аппараты; срок активного существования на орбите; температурный режим.
Keywords: space vehicles; Lifetime in orbit; temperature regime.
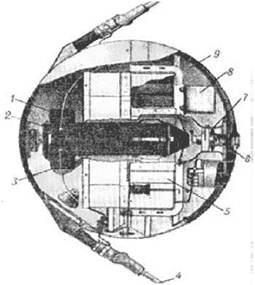
Основными показателями качества космических аппаратов (КА) является их надежность и срок активного существования (САС) на орбите [1]. С целью обеспечения надежной работы на первом спутнике ПС-1 («Простейший спутник первый»), запущенном 4 октября 1957 года, выполненном в виде сферического контейнера диаметром 580 мм, состоящего из двух сферических полуоболочек, изготовленных из листового сплава АМг6 толщиной 2 мм (см. рисунок) [2], использовалась система терморегулирования, при которой тепловой режим внутри объема спутника обеспечивался вентилятором, включавшимся от термореле при температуре, равной или выше 30 °С. При этом циркулирующий в системе терморегулирования азот осуществлял передачу тепла «холодной» задней полуоболочке спутника, излучавшей избыток тепла в космическое пространство. При понижении температуры азота до 20-23 °С вентилятор выключался, что приводило (в отсутствие конвекции) к значительному увеличению теплового сопротивления между радиационной поверхностью и внутренним объемом поверхности корпуса и, таким образом, предотвращало дальнейшее снижение температуры [3].
Срок активного существования спутника ПС-1 на орбите составил 3 месяца: запуск - 4 октября 1957 года, сход с орбиты - 4 января 1958 года.
|
Рис. 1. Конструктивная схема первого искусственного спутника Земли: 1 - сдвоенное термореле системы терморегулирования; 2 - радиопередатчик; 3 - контрольные термо- и барореле; 4 - антенна, 5 - аккумуляторная батарея; 6 - вентилятор; 7 - диффузор; 8 - дистанционный переключатель; 9 - экран [4]
Спутник SESAT-1 стал базой для разработки и изготовления космических аппаратов серии «ЭкспрессАМ», которые сегодня составляют основу орбитальной телекоммуникационной группировки России [5]. Причем согласно Техническим требованиям к космическому аппарату «Экспресс АМУ2» [6], запуск которого запланирован на 2016 год [7], предусмотрен срок его активного существования не менее 15 лет с момента окончательной или условной приемки КА на орбите, что и было спрогнозировано ране [8].
Активная система терморегуляции космического летательного аппарата
Имеются два механических устройства N1, N2 - кривошипно-шатунные механизмы с центробежным насосом. Они превращают поступательное движение штока цилиндра во вращательное движение лопастей насоса. Насосы приводят в движение жидкий теплоноситель в правом и левом трубопроводах. Причем скорость движения жидкости v всегда направлена по часовой стрелке (рис. 1) вне зависимости от направления движения штока.
Трубопровод системы регуляции условно разделен на две части, правая часть имеет длину Lx, левая - Ly.
Скорость жидкости в трубопроводе v системы терморегуляции определим через скорость движения поршня dz/dt:
 , (1)
, (1)
где постоянная b определяется внутренним устройством механизмов N1, N2.
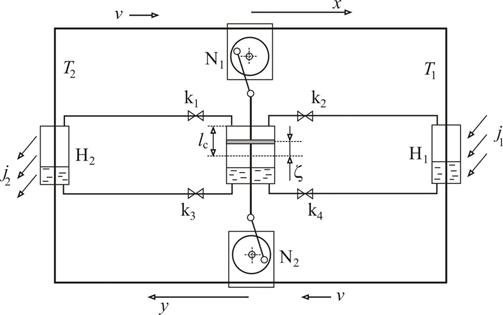
Рис. 2. Кривошипно-шатунные механизмы с центробежным насосом
Термостаты H1 и H2 находятся в хорошем тепловом контакте с трубопроводами, одновременно они генерируют пар или же его переводят в жидкое состояние в зависимости от температуры. Легкокипящая жидкость имеет молярную массу m и теплоту фазового перехода Lm.
Давления в термостатах H1 и H2 рассчитываем по уравнению Клапейрона - Клаузиуса:
 , (2)
, (2)
где температура T1¢ определена в точке x = Lx/2: T1¢ = T1(t, Lx/2), соответственно температура T2¢ определена в точке y = Ly/2: T2¢ = T1(t, Ly/2). Базовое давление p0 = 105 Па; R - универсальная газовая постоянная.
Температура в правом и левом трубопроводах T1(t, x), T2(t, x) определяются решением уравнений
![]() ,
, ![]() .
.
Поток тепла от солнечного излучения полагаем постоянным: j1 = const. Потеря тепла излучением в космическое пространство характеризуется потоком Стефана – Больцмана:
![]() .
.
Здесь s - постоянная Стефана – Больцмана; T0 - равновесная температура реликтового излучения, равная 2.725 K.
Запишем уравнения для температур в виде
![]() , (3)
, (3)
![]() .
.
Уравнения температур дополняются граничными условиями
![]() ; (4)
; (4)
![]() .
.
Для записи уравнений движения поршня цилиндра определим следующий алгоритм действия клапанов ki, i = 1, …, 4. При движении вверх клапаны k1, k4 открыты, клапаны k2, k3 находятся в закрытом положении. При движении вниз клапаны k1, k4 находятся в закрытом положении, а клапаны k2, k3 - открыты. Переключение клапанов происходит при достижении поршня верхней и нижней крайней точки. Масса поршня m, плотность теплоносителя r, эффективное сечение трубопровода системы терморегуляции St, система характеризуется коэффициентом гидравлического сопротивления Cf.
Таким образом, уравнения движения с учетом переключения клапанов можно записать в виде:
![]() , (5)
, (5)
где sign принимает значение +1 (или -1) на начальном этапе расчета. После достижения выполнения равенства z = -d×lc или z = d×lc (0 < d < 1), sign меняет знак: sign ® - sign. Но здесь имеется два возможных технических решения при достижении крайних точек z = -d×lc или z = d×lc:
1) жесткая остановка поршня: координата и скорость мгновенно обнуляются z = dz/dt = 0;
2) мягкая остановка поршня: координата z и скорость dz/dt сохраняют прежние значения и очень короткое время продолжают двигаться по инерции
Давление в цилиндрической камере экспоненциально зависит от температуры. Относительно небольшие изменения температуры могут привести к значительному росту давления за короткий промежуток времени и, как следствие, такому же росту скорости движения поршня. Поэтому для устойчивого и плавного движения поршня требуется сила сопротивления. В данной модели такая сила учитывается коэффициентом k и сомножителем dz/dt.
Численные схемы для решения уравнений.
Для численного решения уравнений (3) применялась неявная схема. Эти уравнения одинакового типа. Поэтому для приведения их разностных форм и общности изложения вместо температур используем символ T, а для свободных членов с потоками тепла – символ F. Таким образом, можем записать
![]() . (6)
. (6)
Пусть время отсчитывается с шагом t, числа шагов нумеруем индексом k. Аналогично переменная x пространственной координаты отсчитывается с шагом h и индексом i. Тогда (6) в разностной форме примет вид
![]() .
.
Отсюда получим
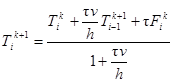 , i = 1, 2, 3, …
, i = 1, 2, 3, …
Для решения уравнения (5) применялся метод Эйлера – Крамера, имеющий второй порядок точности по шагу t.
Работа системы терморегуляции сильно зависит от геометрических размеров камеры и физических свойств легкокипящей жидкости. Ниже на рис. 2 - 5 приведены результаты моделирования системы с рабочей жидкостью циклопентан (С5Н10). Ее молекулярный вес m = 0.07 кг/моль, Равновесная температура кипения Tb = 49.26 °C при 760 мм.рт.ст.; теплота фазового перехода L = 391 кДж/кг; плотность r = 726 кг/м3.
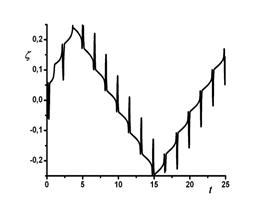

Рис.3. Зависимость z от времени. |
Рис. 4. Зависимость p1/p0 и p2/p0 от времени. |
Остальные параметры следующие: b = 10-9 1/(с×K3), J0 = 10.4 K/с, rc = 0.05 м, rt = 0.005 м, lc = 1.0 м, d = 0.25, b = 50; m = 0.5 кг, k = 150 1/с, Cf = 0.03.
Численное моделирование проводилось в физических переменных. При этом шаг интегрирования по времени t = 2.5×10-5 с. Начальные условия для температур T1 = 312 K, T2 = 322 K; для поршня приняты условия z = 0, dz/dt = 0.
Остановка поршня при достижении крайних точек z = -d×lc или z = d×lc производится в жестком режиме.

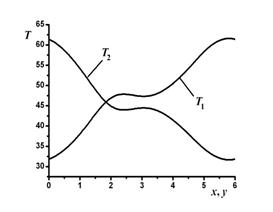
Рис. 5. Зависимость температуры T1¢ и T2¢ (°C) от времени. |
Рис. 6. Распределение температуры (°C) по контуру трубопровода, время t = 25 с. |
На всем этапе расчета наблюдаются сильные и практически периодические колебания давления в камере (рис. 4), поршня (рис. 2) и скорости теплоносителя. Аналогичные колебания имеют место и в каждой фиксированной точке контура трубопровода, в частности, в местах размещения термостатов (рис. 4).
Сближение T1¢ и T2¢ (рис. 4) означает нагрев холодной части системы, и относительное небольшое охлаждение горячей части. Т.е. система терморегуляции в целом выполняет свою функцию.
На рис. 5 изображено пространственное распределение температуры теплоносителя по контуру системы в момент времени t = 25 c. Согласно выбранным началам отсчета координат x, y конечному значению температуры T1(x = 6) соответствует начальное значение температуры T2(y = 0). И наоборот, конечному значению T2(y = 6) соответствует начальное значение T1(x = 0). Таким образом, на рис. 5 изображено распределение теплоносителя по замкнутой линии трубопровода системы терморегуляции.
Модифицированная система терморегуляции.
Приведенные выше результаты показывают неудовлетворительную работу системы: непериодические и резкие изменения параметров (давления p1, p2 скорости v и смещение поршня z) затрудняют использование предлагаемого устройства.
Поэтому схема системы терморегуляции подверглась изменению: добавлены резервуары V1, V2 для относительно плавного изменения давления в цилиндрической камере (рис. 6). Все резервуары имеют одинаковый объем V.
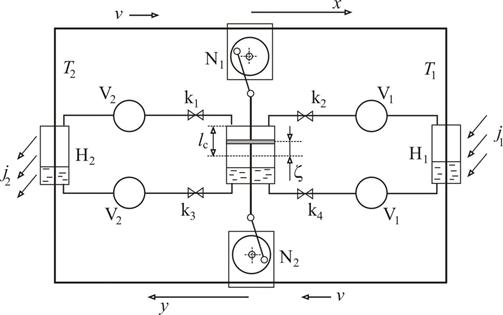
Рис. 7.Модернизированное устройство терморегуляции
Для заполнения резервуаров паром легкокипящей жидкости и установления в них равновесного давления требуется некоторое время. Массовая скорость испарения q (кг/м2с) с поверхности жидкости дается уравнением Герца – Кнудсена [1]
![]() ,
,
где a - коэффициент аккомодации; p - действительное давление паров жидкости; ps - равновесное давление паров при температуре T по закону Клапейрона - Клаузиуса
 .
.
Количество поступающей массы в объем V из поверхности жидкости Sf за единицу времени Dt равно qSfDt. Эта масса должна быть равна приросту массы Dm в объеме V: Dm = qSfDt. Поделив обе части на Dt и устремив к нулю приращения, получим дифференциальное уравнение dm/dt = qSf.
Если пренебречь изменениями объема и температуры по сравнению с изменением давления, то с помощью уравнения Менделеева – Клапейрона pV = mRT/m можно записать
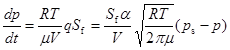 .
.
Это уравнение применяется для правой и левой частей системы. Поэтому теперь давления p1, p2 находим как решения уравнений
 ,
,  , (7)
, (7)
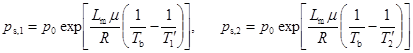 .
.
В дальнейшем при численном моделировании введем параметр c:
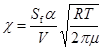 . (8)
. (8)
В приведенных ниже результатах расчета (рис. 7 – 10) принято c = 1. Начальные условия для давлений следующие: p1 = 105, p2 = 0.8×105. Все остальные постоянные параметры остаются неизменными.
Остановка поршня при достижении крайних точек z = -d×lc или z = d×lc производится в жестком режиме.

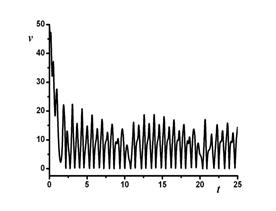
Рис. 8. Зависимость смещения поршня z от времени. |
Рис. 9. Зависимость скорости теплоносителя v от времени. |
Здесь ясно видно качественное изменение в динамике, колебания стали более «мягкими»: сильных и импульсивных движений, подобных удару, теперь уже меньше. Высокочастотные колебания есть, но их амплитуда заметно меньше, чем в предыдущем случае.
Наблюдающиеся частые изменения скорости теплоносителя по сравнению с изменениями координаты поршня легко объяснить: скорость теплоносителя v пропорциональна модулю скорости движения поршня, поэтому частота изменения скорости теплоносителя будет в два раза больше частоты изменения скорости поршня.
По этой же причине частота изменения температуры теплоносителя будет равна частоте изменения ее скорости.
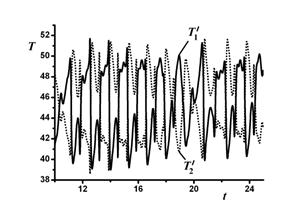
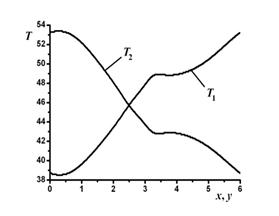
Рис. 10. Зависимость температуры T1¢ и T2¢ (°C) от времени. |
Рис. 11. Распределение температуры (°C) по контуру трубопровода, время t = 25 с. |
Следующее моделирование проведено с параметрами:
b = 10-9 1/(с×K3), J0 = 10.4 K/с,
rc = 0.05 м, rt = 0.005 м, lc = 1.0 м, d = 0.25,
b = 50; m = 0.5 кг, k = 10.0 1/с, Cf = 0.03; c = 0.5.
Начальные условия для давлений следующие: p1 = 0.88×105, p2 = 0.86×105. Как видно, теперь коэффициент сопротивления k уменьшен в 15 раз и c снижен в два раза.
Рассмотрим вначале результаты (рис. 11 – 14) с жесткой остановкой поршня при достижении ею верхних и нижних крайних точек.
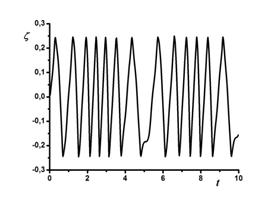

Рис. 12. Зависимость смещения поршня z от времени. |
Рис. 13. Зависимость скорости теплоносителя v от времени. |

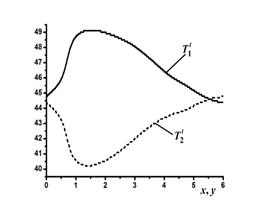
Рис. 14. Зависимость безразмерного давления p1/p0 и p2/p0 от времени. |
Рис. 15. Распределение температуры (°C) по контуру трубопровода, время t = 10 с. |
Если же остановка поршня производится в мягком режиме, то наблюдается качественно другой режим работы регулятора (рис. 15 – 18).


Рис.16. Зависимость смещения поршня z от времени. |
Рис.17. Зависимость скорости теплоносителя v от времени. |
Из приведенных результатов можно заключить, что жесткая остановка поршня вносит регулярность (упорядоченность) в движение поршня. Вносимые условия z = 0, dz/dt = 0 при достижении поршнем крайних точек z = -d×lc или z = d×lc означает воздействие на поршень кратковременного импульса.
В мягком режиме, когда поршень предоставлен самому себе и обращает свое движение только под действием сил давления, динамика системы становится нерегулярной. В некоторые моменты времени, например, между 2.2 и 6.3 секундами (рис. 17) давление p2 становится больше p1.
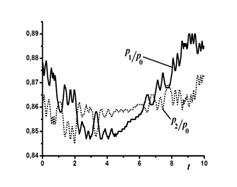

Рис. 18. Зависимость безразмерного давления p1/p0 и p2/p0 от времени. |
Рис. 19. Распределение температуры (°C) по контуру трубопровода, время t = 10 с. |
Но расчет, проведенный до t = 25 с, показал восстановление регулярного режима работы системы: смещение поршня становится периодическим, скорость теплоносителя не характеризуется слишком большими скачками и давление p1 всегда больше p2.