МЕТОДЫ ОБЕСПЕЧЕНИЯ ФУНКЦИОНАЛЬНОЙ УСТОЙЧИВОСТИ НА ОСНОВЕ ОБРАТНЫХ СВЯЗЕЙ

Одной из важнейших сфер деятельности человека является информационная инфраструктура. Изначально для этого использовалась телеграфная сеть, но прогресс не стоял на месте. Со временем стали появляться телефоны, радио, телевидение, компьютеры. Теперь любые сведения, созданные в электронном виде, могут быть доставлены до адресата без помощи специально обученного человека.

Связь субъектов страны, международная связь работает на основе многоканальных телекоммуникационных систем (МТС). Для этого применяются аналоговые и цифровые устройства. С их помощью можно передавать аудио, видео и мультимедиа. Людям стали доступны выход в Интернет, сотовая связь и множество других услуг.

Надежность – свойство объекта сохранять во времени в установленных пределах все параметры, обеспечивающие выполнение требуемых функций в заданных условиях (условиях применения, технического обслуживания, ремонта, хранения и транспортирования).

Надежность является одним из свойств, характеризующих качество изделий. Под качеством изделий понимается совокупность свойств изделий, обуславливающих его пригодность удовлетворять определенные потребности в соответствии с его назначением.

Показателем надежности называется количественная характеристика одного или нескольких свойств, составляющих надежность объекта.

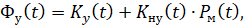                                                                                         (1)

где 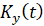 – исходная устойчивость;

 – приращение функциональной устойчивости (Ф.У.) за счет реализации определенного метода.

Формула (1) является функционалом комплексного показателя функциональной устойчивости системы.

Это так называемая «великая формула жизни». Она описывает весь жизненный цикл всех систем.

Этот показатель называют также генеральным критерием Ф.У. системы. Он нормирован от 0 до 1.

Важнейшей задачей анализа систем линейного тракта является решение вопроса об их устойчивости. Техническое понятие устойчивости отражает свойство технической системы не только стабильно работать в нормальных режимах, но и «не уходить вразнос» при отклонении всевозможных параметров системы от номинала и влиянии на систему дестабилизирующих воздействий, то есть способности системе возвращаться к равновесному состоянию, из которого она выводится возмущающими или управляющими воздействиями.

Устойчивость системы – техническое требование в ряду более сложных требований, связанных с показателями качества и точности передачи данных.

Рассмотрим понятие устойчивости системы более детально.

Система находится в состоянии равновесия, если при отсутствии воздействия на систему возмущающих факторов ошибка регулирования (разность между заданным и фактическим состоянием системы) стремится к нулю. Под устойчивостью понимается способность системы возвращаться в равновесное состояние после окончания действия возмущения, нарушив это равновесие.

Неустойчивая система после воздействия возмущения удаляется от равновесного состояния или начинает совершать вокруг него колебания с нарастающей амплитудой. Таким образом, аппаратура выходит из строя.

Возникновение неустойчивых (расходящихся) колебаний в системе можно проследить на примере системы с обратной связью.

В основе метода обратных связей лежит идея сочетания функциональной диагностики и автоматического повторного включения с возможной перестройкой структуры системы.

• Метод обратных связей в нерезервированных устройствах сети.

Обобщенная система обеспечения функциональной устойчивости возможна при следующих допущениях – воздействия являются безошибочными.

Причиной алгоритмических сбоев является неустойчивая работа самого контролирующего устройства.

Такое предположение основано на том, что предыдущие устройства, выходные сигналы которых являются сигналами для контролирующего устройства (КУ), также обеспечиваются только системой функциональной диагностики (СФД) либо СФД в сочетании с системой автоматического повторного включения (САПВ).

Это исключает случаи поступления ложных входных воздействий на КУ.

Следует отметить, что математические модели метода обратных связей основаны на том, что СФД обеспечивает 100%-ное обнаружение алгоритмических сбоев. Следовательно, в соответствии с общим выражением для генерального критерия вероятность просто будет равна вероятности метода.

Функциональная устойчивость (ФУ) контролирующего устройства обеспечивается методом попыток. САПВ прекращает свою работу в том случае, если очередная попытка оказалась удачной. СФД фиксирует эту попытку, а КУ реализует очередной алгоритм без сбоев.

Есть два условия достижения ФУ:

1. условная вероятность устранения сбоев каждой попытки одинаковая;
2. от попытки к попытке вероятности либо возрастают, либо уменьшаются.

Исключением является случай, когда вероятность изменяется произвольным образом.

Так как данные, полученные в ходе эксперимента, ограничены, то предъявляемые требования к аппроксимирующей функции должны быть достаточно высокими. Поэтому определенный интерес представляет получение законченных решений с учетом предъявляемых требований. Для этого ищется корректирующий коэффициент – C.

Но в основном при расчетах использование метода коррекции носит «грубый характер», а точность определения должна быть высокой.

• Метод обратных связей в резервированных устройствах сети.

При первом алгоритме предполагается, что все САПВ последовательно друг за другом делают по одной попытке, затем по другой и так далее до устранения алгоритмического сбоя либо до истечения принятого числа повторений.

Считается также, что вероятности устранения сбоев от попытки к попытке в пределах каждой системы АПВ, а также от одной САПВ к другой (в совокупности за допустимое число попыток) могут быть как постоянными, так и переменными – убывать, возрастать или изменяться произвольным образом.

При всем многообразии возможных частных случаев совокупность систем АПВ для определения вида закона распределения вероятности устранения сбоев с m попыток; т.е. F(m), можно представить в качестве одной САПВ с числом попыток, равным M (считая, что M общее для всех систем АПВ), и вероятностью устранения сбоев в каждой попытке, равной результирующей вероятности единичных попыток всех систем.

Вероятность устранения алгоритмических сбоев обобщенной системой АПВ в m-й попытке будет:

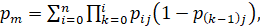                                                                                        (2)

где значения j соответствуют значениям m.

В основном формулы, используемые для расчета первого алгоритма, являются частными случаями формулы, описывающей в общем виде закон распределения вероятности устранения алгоритмических сбоев несколькими САПВ.

Для определенных систем АПВ, у которых известны вероятности, значение N представляет собой постоянную величину, то есть N = const.

Когда в аппроксимирующую функцию вводится корректирующий член в виде постоянного числа C, следует учитывать, что сама аппроксимирующая функция должна быть положительна, а функция распределения – меньше 1.

Когда функция будет получена (она должна иметь логарифмическую зависимость), графики коррекции будут совпадать с графиками для нерезервируемых систем и среднее значение в этом случае будет зависеть от времени .

В заключение рассмотрения первого алгоритма работы нескольких систем АПВ необходимо сделать следующее замечание. В начале рассмотрения было сделано предположение о том, что все системы АПВ имеют одно и то же значение числа M. Однако в общем случае этого может и не быть, т.е. вероятности устранения алгоритмических сбоев в каждой попытке обобщенной системой АПВ могут выражаться иначе.

Однако учет возможности такого варианта не влияет на полученные результаты. Действительно, всегда можно принять в качестве общего M его максимальное значение из числа, считая при этом равными нулю значения вероятностей.

Суть в том, что при первом алгоритме все имеющиеся САПВ друг за другом делают по одной попытке, затем по другой, по третьей и так далее, пока не будет устранен алгоритмический сбой, либо до истечения принятого числа повторений.

При втором алгоритме берется несколько САПВ. Первая система делает полное (принятое для систем число попыток), аналогичным образом работает вторая, третья и так далее либо до устранения сбоя, либо до истечения числа попыток. Вероятность устранения ошибок может быть как постоянная, так и перемененная – убывать, возрастать. В качестве числа попыток можно взять число, равное АПВ(n+1), а вероятность устранения сбоев – результирующую вероятность всех попыток.