ЧАСТНЫЕ РЕШЕНИЯ НЕВОЗМУЩЕННОГО УРАВНЕНИЯ ШТУРМА-ЛИУВИЛЛЯ НА ПОЛУОСИ

PARTIAL SOLUTIONS OF THE UNPERTURBED STURM-LIOUVILLE EQUATION ON THE SEMIAXIS

Ainur Qasimova

Doctor of Philosophy in Mathematics, Ganja State University, Azerbaijan, Ganja

Аннотация. В развитии многих важных направлений математики и физики большую роль сыграли понятия и методы, зародившиеся в процессе изучения уравнений Штурма – Лиувилля  . В настоящей статье исследовано решение обратной задачи для возмущенного уравнения Штарка с растущим потенциалом на бесконечном интервале . Получена формула для вычисления производной от спектральной функции оператора Штарка, доказано существование оператора преобразования с условием на бесконечности.

Abstract. In the development of many important areas of mathematics and physics, the concepts and methods that arose in the process of studying such simple objects as the Sturm-Liouville -  equation played an important role. In this article, we study the solution of the inverse problem for the perturbed Stark equation with a growing potential on an infinite interval . A formula is obtained for calculating the derivative of the spectral function of the Stark operator, and the existence of a transformation operator with the condition at infinity is proved.

Ключевые слова: уравнения Штурма-Лиувилля, равенство Парсеваля, оператор преобразования, производная спектральной функции.

Keywords: Sturm-Liouville equations, Parseval equality, transformation operator, derivative of a spectral function.

1. Частные решения уравнения      .

В данной работе расматривается граничная задача вида:

      0∞                                                                                       (1.1)

                                                                                                             (1.2)

при финитном потенциале p(x) [1,4].

Находится и исследуется решение уравнения (1) при p(x)=0  (x > а).

                                                                                               (1.3)

(-функция Ганкеля).

Лемма 1.1. Уравнение (1.1) имеет решение  принадлежащее пространству L₂[0,∞) при Imλ>0.

Исследуем некоторые частные решения уравнения 

.                                                                                                       (1.4)

С этой целью положим               

                                                                                                     (1.5)

Функцию (x) определяем из того условия, что коэффициент при искомой функции (x) в дифференциальном уравнении уничтожился бы член, содержащий х. Для этого достаточно (x) выбрать следующим образом:   . Тогда                           

                                                                                                     (1.6)

где для  имеет место уравнение

                                                                                             (1.7)

Решая это уравнение получаем [1]:

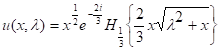                                                                                         (1.8)

Подставляя (1.8) в формулу (1.5) получим решение уравнения (1.4)

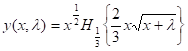                                                                                                (1.9)

То есть, линейно-независимыми решениями уравнения (1.4) являются функции [3]

                                                                                           (1.10)

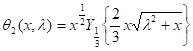                                                                                            (1.11)

2. Равенство Парсеваля.

Введем обозначения

                                                                                                     (2.1)

Вычислим вронскиан решений (1.12) и (1.13)

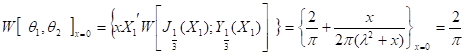
То есть ,                            

                                                                                                     (2.2)

Здесь мы учитываем, что вронскиан решений равно  т.е. [3]

                                                                                                      (2.3)

Обозначим через  - решения уравнения (1.6) с начальными условиями

                                                                                                 (2.4)

                                                                                                 (2.5)

Очевидно,что

                                                                                       (2.6)

Учитывая условия (2.4), (2.5), находим

Подставляя эти значения в (2.6) получим

                                                                                (2.7)

Учитывая асимптотику функций   [1],

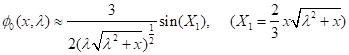
Аналогично находим асимптотику 

Отметим, что функция     

                                                                                                 (2.8)

содержит множитель  

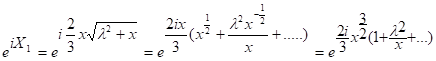
который при  экспоненциально убывает при . Итак, лемма 1 доказана.

Очевидно, что является функцией Вейля [3], поэтому она может отличаться от  лишь постоянным множителем

   , c=const                                                                                (2.9)

Отсюда . Тогда производная  от спектральной функции, порожденная уравнением  (1.6) и граничным условием  определяется как известно [4] следующим образом :.

Поэтому

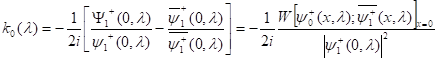                                                                 (2.10)

Учитывая, что  после некоторых вычислений получим

                                                                                          (2.11)

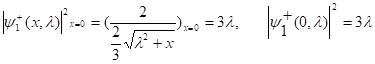                                                                             (2.12)

Подставляя [1,3]  (2.11), (2.12) в (2.10)   получим   

                                                                                                      (2.13)

Поэтому формула разложения выглядит так

                                                                                      (2.14)

Лемма 2.1      Производная от спектральной функции, порожденная задачей ,                            определяется по формуле

                                                                                                  (2.15)