СРАВНЕНИЕ МЕТОДА ПОИСКА

Аннотация. Был проведён анализ и исследование двух алгоритмов поиска, блочного и бинарного. С помощью программ и замера процессорного времени подсчитана эффективность каждого.

Ключевые слова: блочный поиск, двоичный поиск, эффективность, анализ.

Поиск – процесс нахождения конкретной информации в ранее созданном множестве данных. Обычно данные представляют собой записи, каждая из которых имеет хотя бы один ключ.

Ключ поиска – это поле записи, по значению которого происходит поиск.

Ключи используются для отличия одних записей от других. 

Работа блочного поиска заключается в том, что массив делится на блоки, наилучший вариант количество блоков – 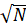, а наихудший – .

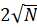I этап: Аргумент поиска сравнивается с последними элементами каждого из блоков, если не будет получено значение, то результат поиска будет отрицательным и программа будет приступать ко II этапу.

II этап: Осуществляется последовательный поиск в найденном блоке в направлении от последней к первой записи в блоке.

Чтобы мы могли использовать бинарный или двоичный поиск, для начала мы должны отсортировать сам массив.

Рассмотрим двоичный(бинарный) поиск, двоичный поиск делит массив на две части, затем аргумент поиска сравнивается со средним элементом массива, если значение аргумента поиска меньше среднего элемента, то мы рассматриваем все элементы массива от 0 до N/2, где N – это количество элементов массива, а если аргумента поиска больше текущего элемента, то рассматривается элементы массива от N/2 до N. Таким образом, осуществляется последовательное деление пополам интервала поиска до тех пор, пока не будет найден искомый элемент или длина последовательности не станет равной единице.

Работа двух программ заключается в нахождении данного элемента, в массиве с размерностью: 100, 1000, 10000 и 100000.

А также подсчёта времени с помощью библиотеки thread и средних количества сравнений для двоичного поиска – 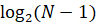, а для блочного поиска – .

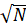Таблица 1.

Результаты со средним количество сравнений.

Таблица 2.

Теперь рассмотрим опыт с фактическими сравнениями

Вывод:

По результатам эксперимента можно сделать вывод, что для поиска случайного значения в отсортированном массиве, более эффективный — это двоичный(бинарный) поиск.