О ПЛАНКОВСКОЙ LT СИСТЕМЕ ЕДИНИЦ

ABOUT THE PLANCK LT SYSTEM OF UNITS

Konstantin Nikonenko

Pensioner, Russia, Moscow

Аннотация. В статье представлена Планковская LT система единиц, сформированная на основе размерностей физических величин кинематической системы единиц Р.О. ди Бартини. Приведены значения единиц измерения, основных констант, переводных коэффициентов в соотношении с Международной SI и Гауссовой системой, обеспечивающие перенос исходных данных и результатов расчетов между этими системами единиц без потери точности вычислений.

Abstract: The article presents the Planck LT system of units, formed on the basis of the dimensions of physical quantities of the kinematic system of units by R.O. di Bartini. The values of units of measurement, basic constants, conversion coefficients in relation to the International SI and Gaussian system are given, ensuring the transfer of initial data and calculation results between these systems of units without loss of calculation accuracy.

Ключевые слова: Планковская система единиц LT; кинематическая система единиц LT; Международная SI; Гауссова система единиц.

Keywords: Planck system of units LT; kinematic system of LT units; International SI; Gaussian system of units.

Введение

Двумя наиболее распространенными системами единиц измерения, используемыми сегодня, являются международная система единиц (далее SI) и Гауссова система (далее G). Эти системы единиц имеют одинаковую размерность механических единиц, но отличаются размерностью электромагнитных единиц и, соответственно, рядом уравнений связи.

Система Планковских единиц не имеет широкого распространения, однако, как и другие естественные системы единиц, она с большим успехом применяется в теоретической физике, поскольку в ней уравнения существенно упрощаются, их запись освобождается от излишних коэффициентов.

Кинематическая система единиц, предложенная Р.О. ди Бартини [2], опирается только на две размерности: пространственной протяженности L и длительности во времени T. Согласно [2] единицы длины и единицы времени квантуются.

В предлагаемой вашему вниманию статье представлена Планковская LT система единиц, сформированная на основе размерности кинематической системы единиц Р.О. ди Бартини при условии, что квантами протяженности и длительности являются, соответственно, Планковская длина  и Планковское время , и ее соотношение с Международной SI и Гауссовой системой. В отличие от [2] время одномерно.

При дальнейшем изложении используем традиционные обозначения физических величин, которые для избежания путаницы пометим верхним индексом SI – для международной системы единиц, G – для Гауссовой системы, LT – для кинематической системы единиц (по Р.О. ди Бартини) и PLT – для Планковской LT системы единиц, PLTSI – для идентичной SI системы PLT и PLTG для идентичной G системы PLT.

Система единиц PLT - планковская интерпретация кинематической системы единиц Р.О. ди Бартини.

Согласно [2, 4] размерность массы в системе LT имеет вид , т.е. планковская масса  , где  – планковская длина,  планковское время. Согласно [1] планковский заряд также имеет размерность , соответственно .

Размерность силы в системе LT [2] имеет вид . Поскольку планковское ускорение , то согласно Второму закону Ньютона планковская сила  .

Закон всемирного тяготения (здесь и далее уравнения связи и соотношения констант приведены в соответствии с [10]) для планковских величин примет вид

т.е. равенство выполняется только при условии, когда гравитационная постоянная Ньютона для системы LT  .

Закон Кулона для планковских величин примет вид

т.е. равенство выполняется только при условии, что постоянная Кулона для системы LT  .

Планковский ток — это ток, переносящий один планковский заряд за одно планковское время – т.е. .

Эквивалентное определение: планковский ток — это постоянный ток, который, протекая в двух прямых параллельных проводниках бесконечной длины, расположенных в вакууме на расстоянии планковской длины друг от друга, создаст между этими проводниками силу, равную планковской силе на каждый участок длины проводников, равный планковской длине: соответственно:

Таким образом, равенство выполняется только при условии .

Переводные коэффициенты между системой PLT и системами единиц Гаусса и SI

Для осуществления дальнейших преобразований определим коэффициенты для перевода значений массы и электрических зарядов между системой PLT и системами G и SI.

В SI, также как и G планковская масса и планковская длина имеют значения:

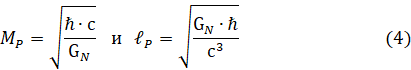
тогда, гравитационная постоянная Ньютона и планковская масса примут, соответственно, значения:

Переводной коэффициент есть отношение между двумя единицами измерения одной и той же величины и по определению должен иметь точное значение.

Переводной коэффициент  (также как и ) есть отношение тождественных величин планковской массы выраженный в единицах пространственной протяженности и длительности по времени к значению в единицах массы соответствующей системы единиц:

Планковский заряд в SI и G определяются различным образом и имеет значение, соответственно:

Переводной коэффициент  и есть отношение тождественных величин (планковского заряда) выраженного в единицах пространственной протяженности и длительности по времени к его значению в единицах заряда соответствующей системы единиц (назовем эту величину постоянной электрического заряда):

Теперь перепишем уравнения (1), (2), (3) после преобразования в общем виде с помощью переводных коэффициентов соответственно для SI и G:

Для расчета гравитационной постоянной:

В SI:

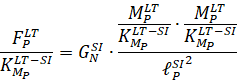
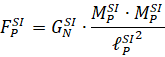
Следовательно

В G:

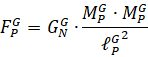
Следовательно

Для расчета постоянной Кулона:

В SI:

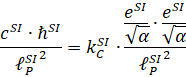
Следовательно

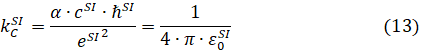
И, соответственно,

Если осуществить обратное преобразование, то диэлектрическая проницаемость вакуума для уравнений связи PLTSI получит значение

.

В системе G

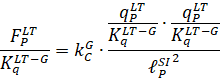
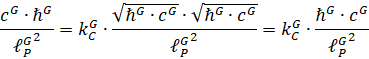
Откуда

Таким образом, имеют место соотношения:

Иначе говоря, постоянная Кулона для любой системы единиц равна отношению переводного коэффициента массы к квадрату переводного коэффициента электрического заряда, т.е. отношению гравитационной постоянной Ньютона к квадрату постоянной электрического заряда.

Таким образом существует механизм для точного соотношения единиц упомянутых систем единиц. Единственным препятствием для выполнения точных расчетов является точность определения планковской длины, ограниченная экспериментально определенным значением и точностью гравитационной постоянной Ньютона

Причем последние экспериментальные определения  дают расхождение до 0,05% ее значения. Это свидетельствует о том, что в различных существующих методах могут быть необнаруженные систематические ошибки. Так, в [14] сообщается, что достигнутый результат измерения  представляет два варианта, каждый из которых в отдельности имеет в два раза лучшую относительную стандартную неопределенность, но значение этих результатов лежат на противоположных границах стандартного отклонения рекомендуемого CADATA значения.  Кроме того, на данных, полученных с 1985 по 1996 г. в работе [3] достоверно выявлены ритмические изменения результатов измерений . Таким образом, как полагают авторы этой статьи: «Разумно предположить, что этот анализ выявляет не изменение величины физической константы - гравитационной постоянной, а действие каких-то неучитывемых исследователями факторов, прямо или косвенно влияющих на результаты измерений», т.е. экспериментальные методы определения этой константы для уточнения значения планковской длины на современном этапе являются малоперспективными.

Однако в [6] предложен подход к уточнению планковской длины путем создания поля значений планковских длин с использованием уравнений связи [10] и рекомендуемых [11] значений физических констант, определенных как точные или с существенно большей точностью чем , с учетом границ стандартной неопределенности этих значений. Массив полученных значений обработан в соответствии с порядком оценки стандартной неопределенности типа А [1]. Кроме того, использован алгоритм рекурсивных расчетов. В результате получено значение  со стандартной неопределенностью  и  относительной стандартной неопределенностью Аналогичным образом уточнено значение постоянной тонкой структуры  со стандартной неопределенностью  и относительной неопределенностью . Для дальнейших расчетов в рамках этой статьи будут использованы именно эти значения.

Уточнение переводных коэффициентов между величинами единицами SI и G

В соотношении единиц измерения SI и G в качестве коэффициента входит безразмерное значение скорости света . Для возможно точного переноса исходных данных или результатов вычислений из одной системы единиц в другую важно, чтобы это отношение имело максимально точное значение. Однако, уже соотношение планковского заряда в франклинах к панковскому заряду в кулонах демонстрируют заметное отличие

Для устранения этого отличия и использования существующих коэффициентов перевода значений электромагнитных величин между SI и G (как и для других систем единиц семейства SGC) с максимальной точностью необходимо и достаточно директивно установить фундаментальную константу элементарного заряда в SI в значении:

Что является лишь уточнением установленного в SI значения фундаментальной константы элементарного заряда  .

Однако такое изменение в SI в обозримом будущем является проблематичным, поэтому для переводных коэффициентов между значениями G и SI, связанными с электромагнитными величинами для обеспечения максимально высокой точности целесообразно использовать поправочный коэффициент электрического заряда  (в соответствии со степенью основной электрической единицы в SI (A - ампера), входящей в значение переводимой величины):

Величину  допустимо полагать точной, поскольку стандартная неопределенность для нее рассчитанная с учетом значения постоянной тонкой структуры [6], как суммарная стандартная неопределенность [1] по формуле

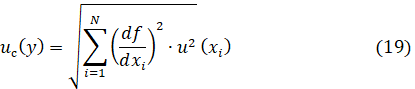
имеет значение .

Необходимо отметить, что именно при применении  постоянная Кулона  приобретает для SI теоретически точно определенное значение [9]:

Т.е. аномалия в единицах SI, связанна не с экспериментальными ошибками при определении одной из фундаментальных констант пропорциональности  , как утверждается в [12], а со значением элементарного заряда в SI, выбранным в качестве точного.

Значения единиц измерения, констант и их соотношения в системах единиц SI, G, PLT, PLTSI и PLTG

Руководствуясь вышеприведенными результатами и формулой расчета стандартной неопределенности расчетных данных, данными Приложения по единицам измерения [12] и размерностью физических величин в системе LT [2] сформирована Таблица 1, в которой приведены значения основных единиц измерения, основных констант, коэффициентов пропорциональности уравнений связи и их соотношения для пяти рассматриваемых систем единиц (SI, PLTSI, PLT, PLTG и G). Расчеты проводились с использованием Mathcad 15.

Для сравнения в Таблице 1 также приведены значения физических констант и планковских величин согласно рекомендациям CODATE [11], и оценка разности между рекомендуемым CODATE значением, обозначенным в таблице как , и расчетным значением, обозначенным в таблице как A в процентах к относительной стандартной неопределенности соответствующего значения

Кроме того, для наглядности приведены результаты перевода соответствующих расчетных значений из системы SI в G и G в SI (в Таблице 1 обозначены (А)₁).

Таблица 1.

Результаты перевода соответствующих расчетных значений из системы SI в G и G в SI

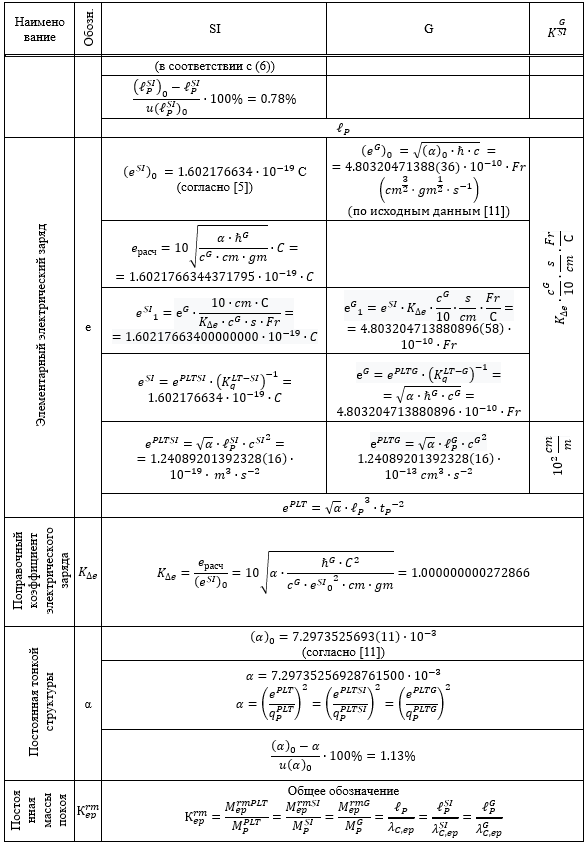
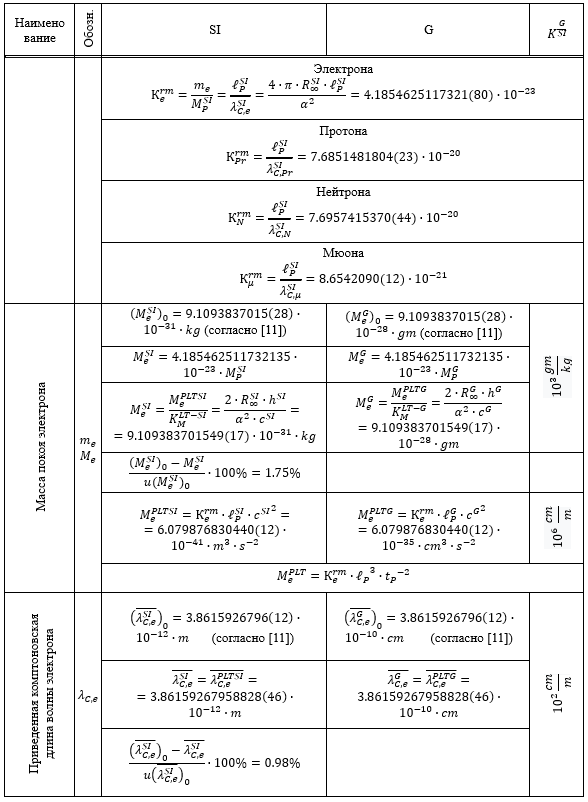
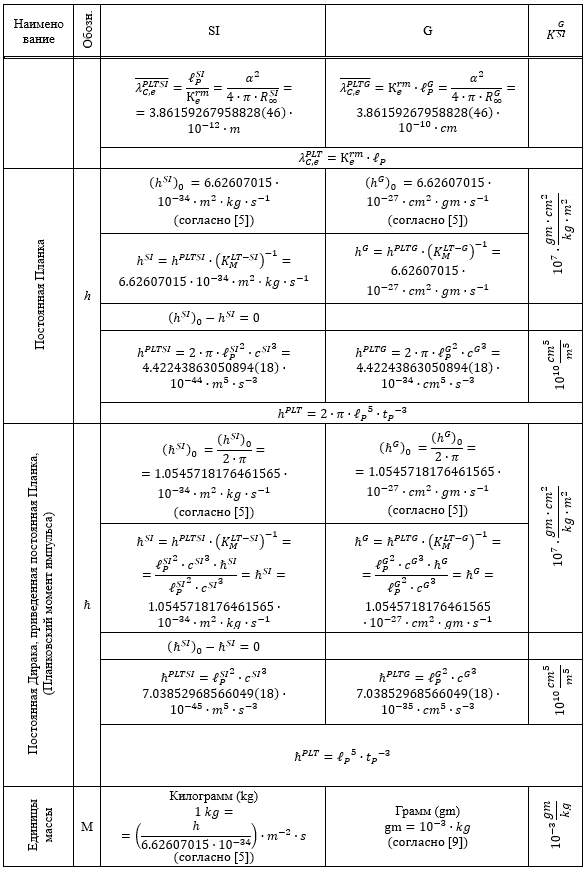
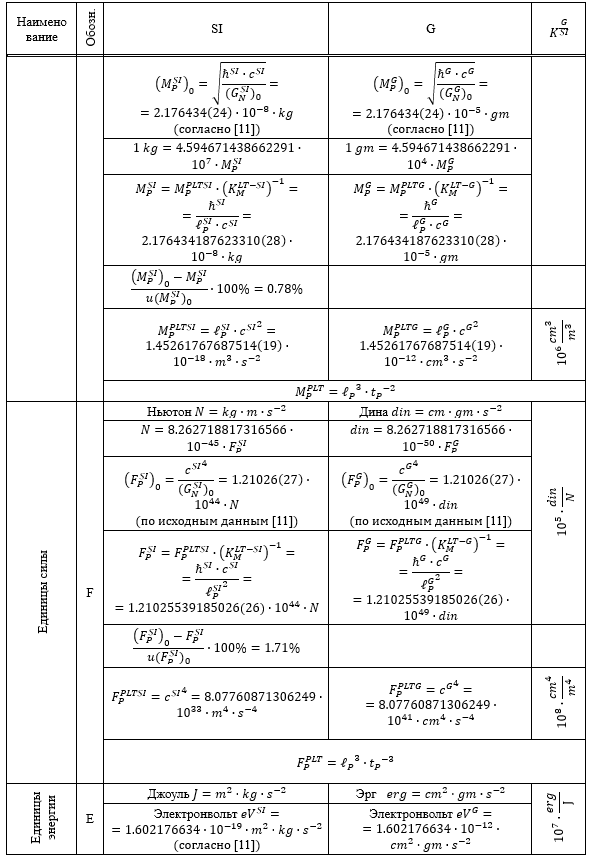
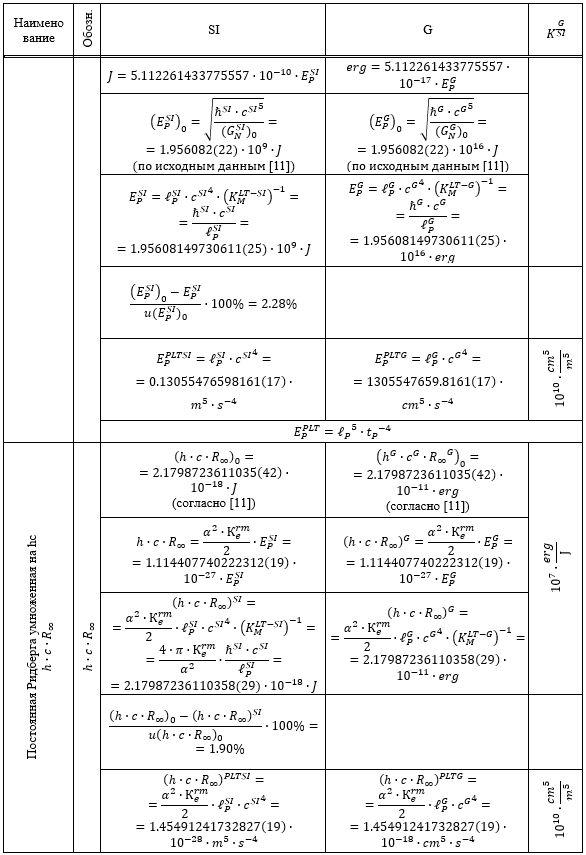
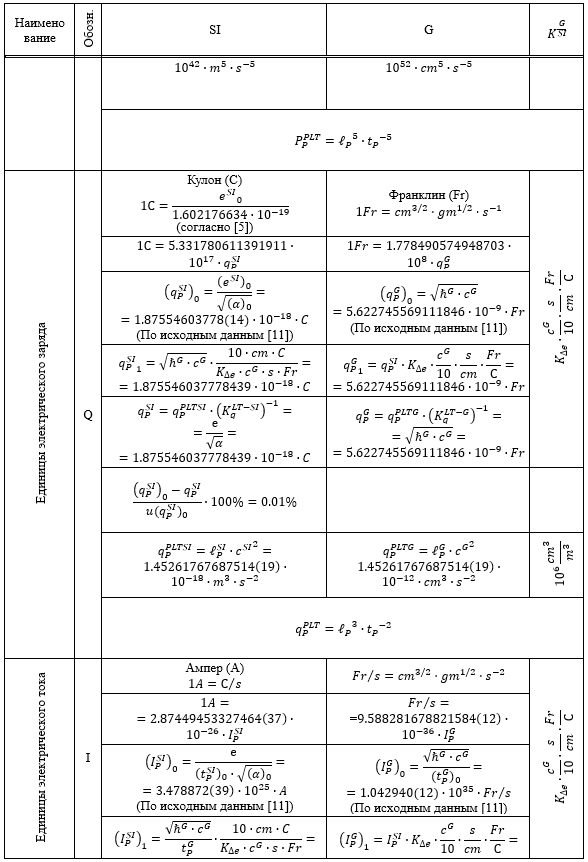
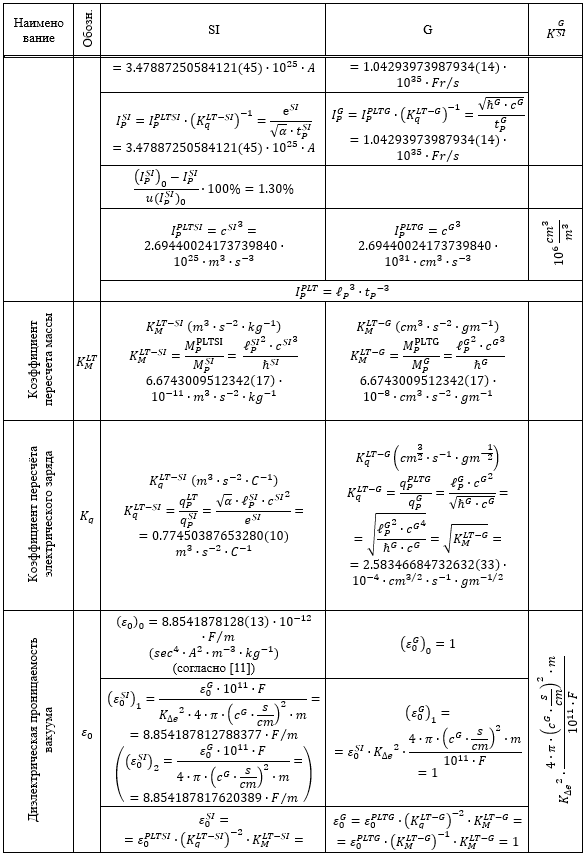
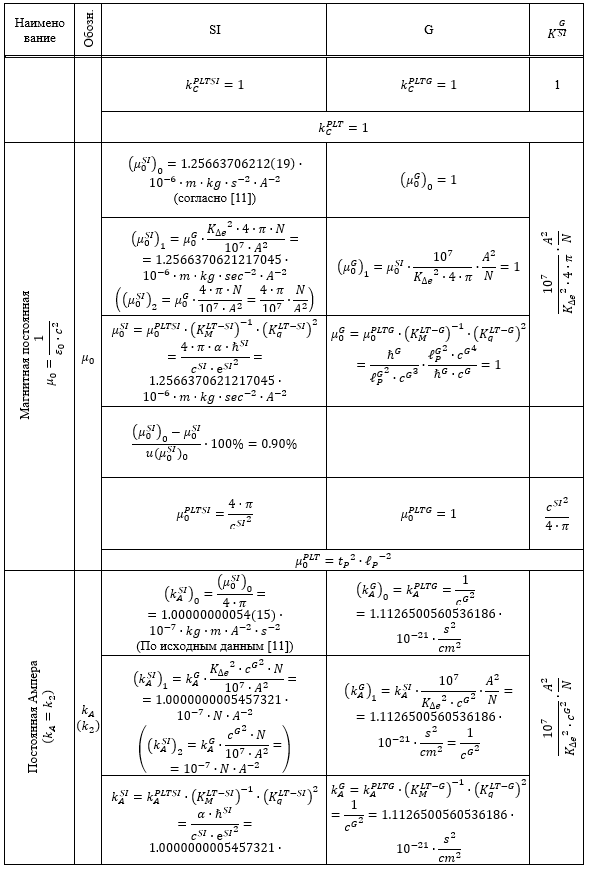
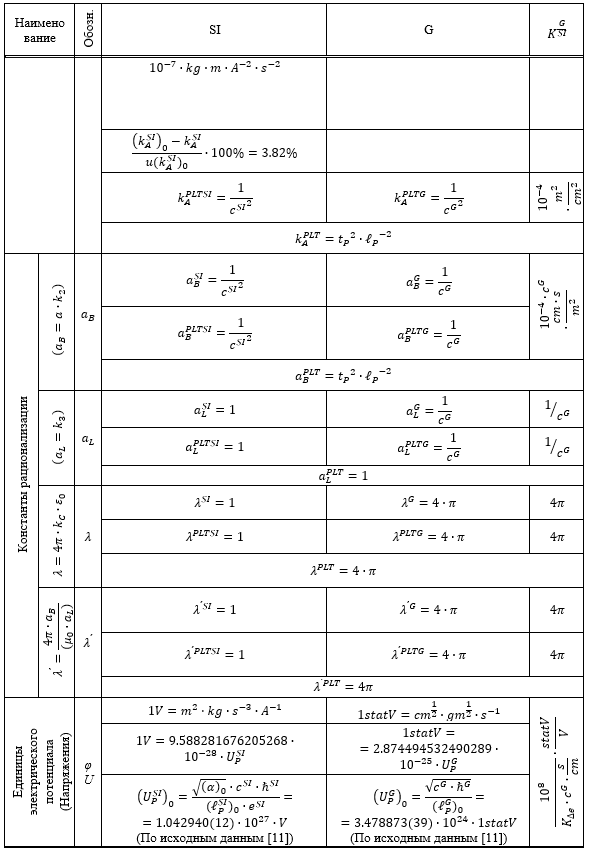
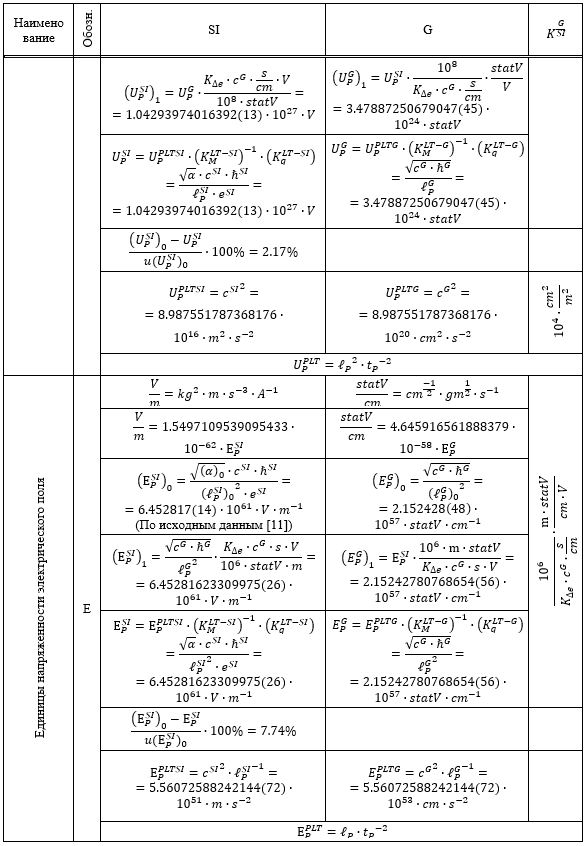
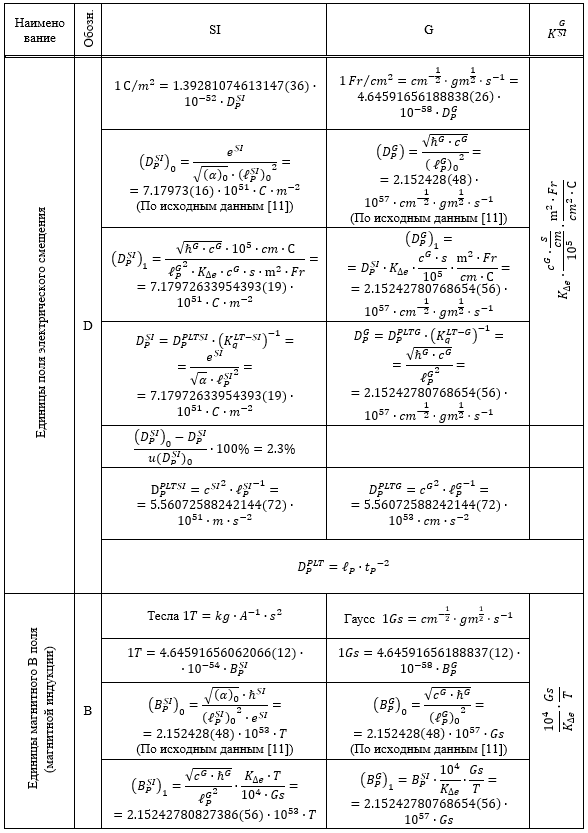
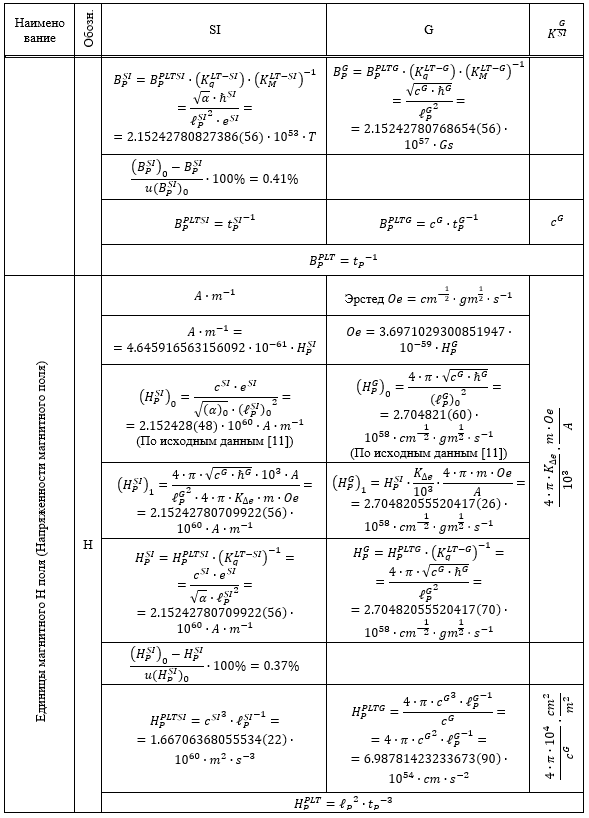
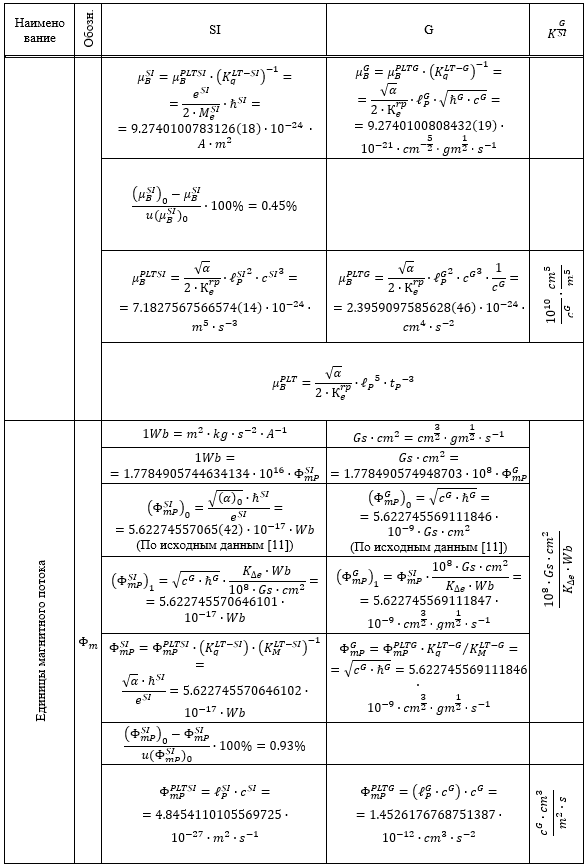
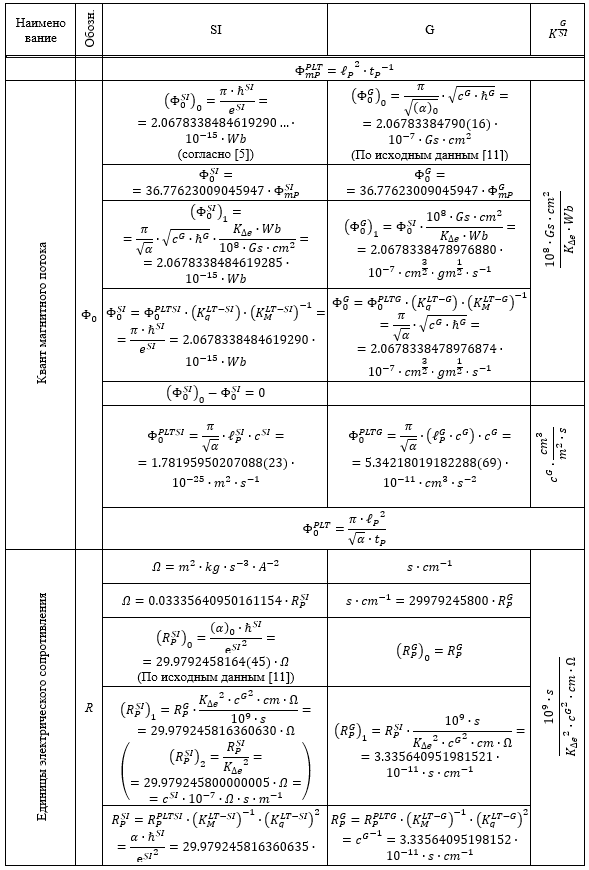
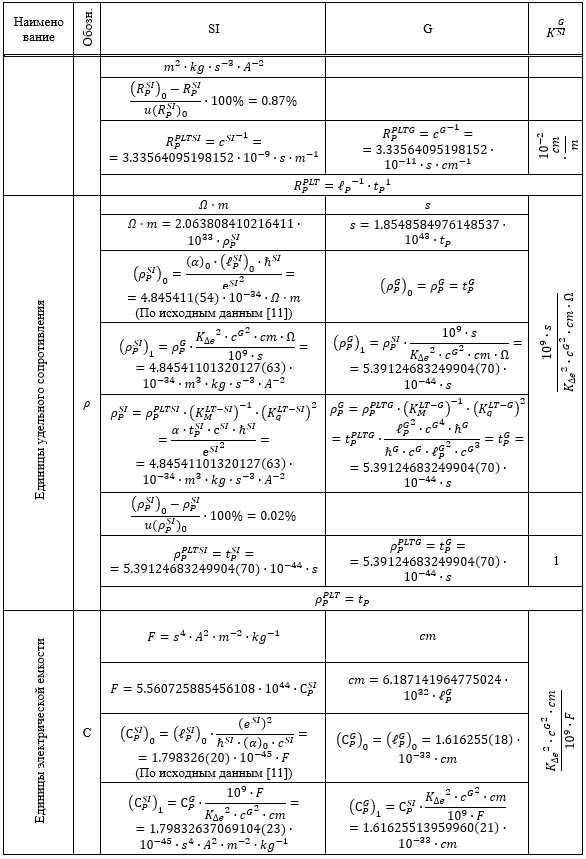
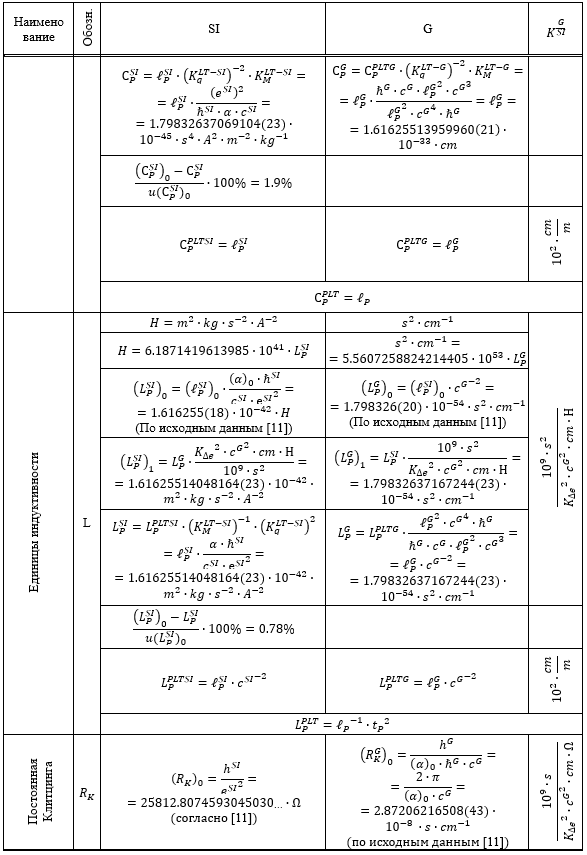
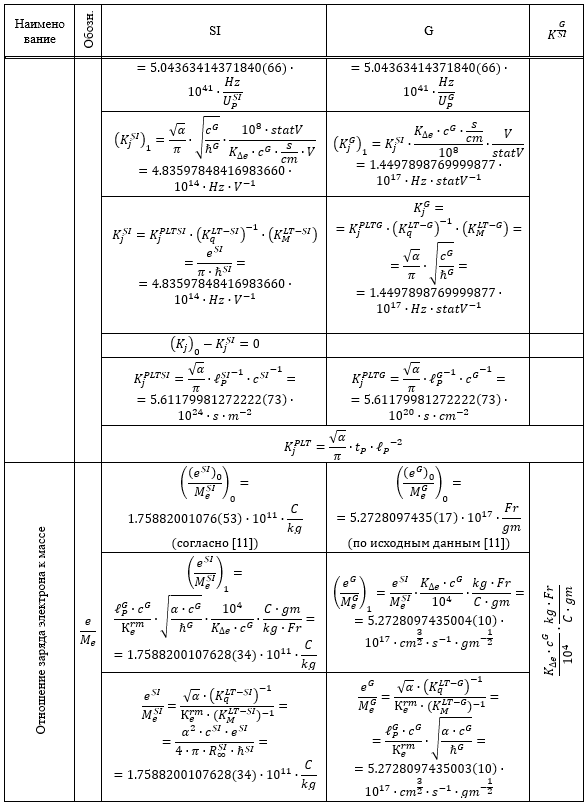
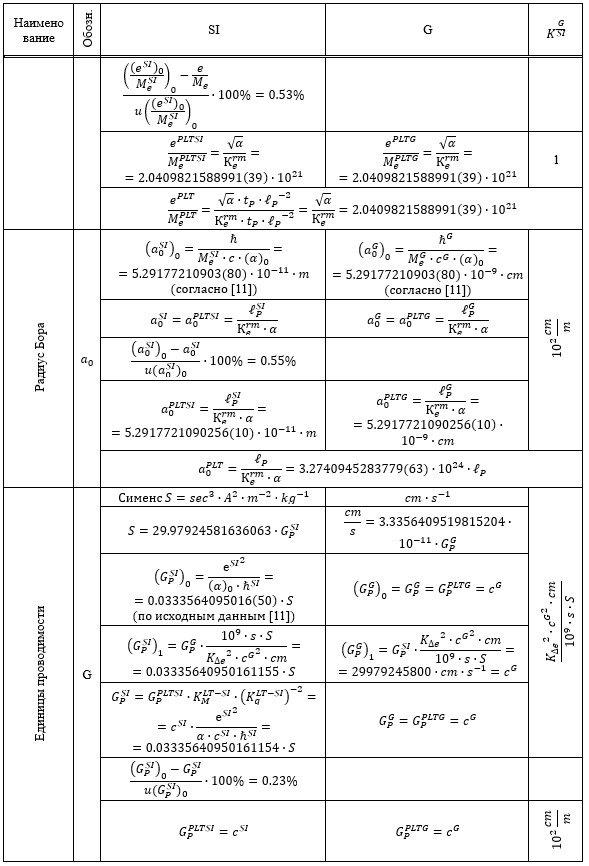
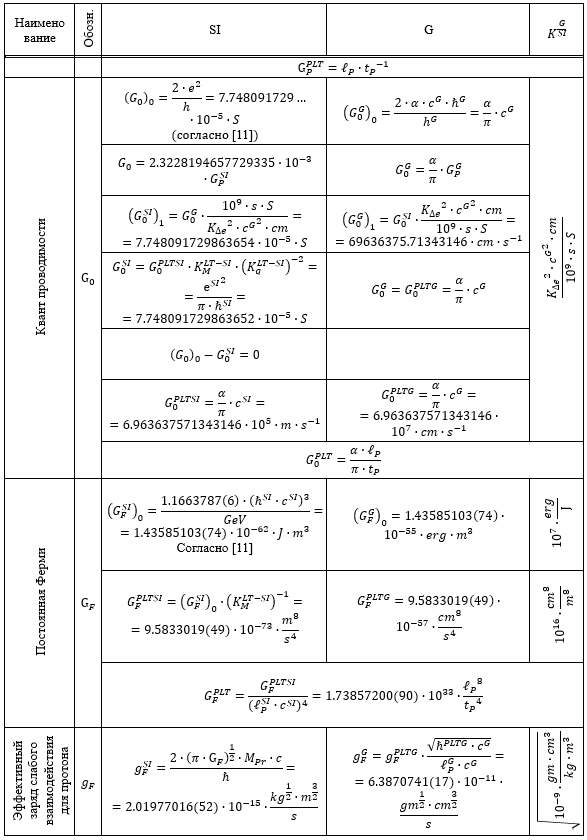
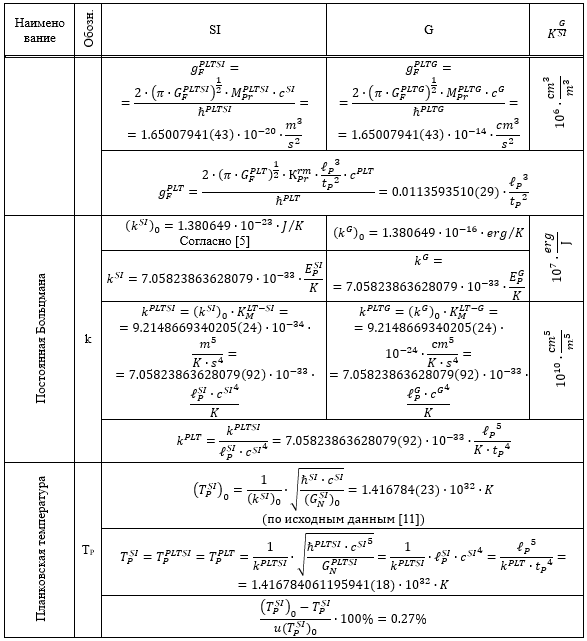
Из приведенных в Таблице 1 данных следует, что все пять систем единиц связаны между собой однозначным и точным соответствием.

При этом расчетные значения имеют отклонения от рекомендуемых CODATE  [11] значений не более 7.74% их стандартной неопределенности.

То есть исходные данные и результаты расчетов, полученных в одной системе единиц, могут быть использованы в другой без потери точности вычислений. 

Так, например, геоцентрическая гравитационная постоянная Земли согласно данным МАС 2016 года [15] имеет значение . Используя переводной коэффициент массы  получаем значение массы Земли

,

что на 4 порядка точнее значения массы Земли, представленного в этом же документе, но рассчитанного с использованием рекомендуемого CODATE  [11] значения гравитационной постоянной Ньютона,  а отклонение от значения MAC  составляет 5.4% его стандартной неопределенности.

Формы электромагнитных уравнений

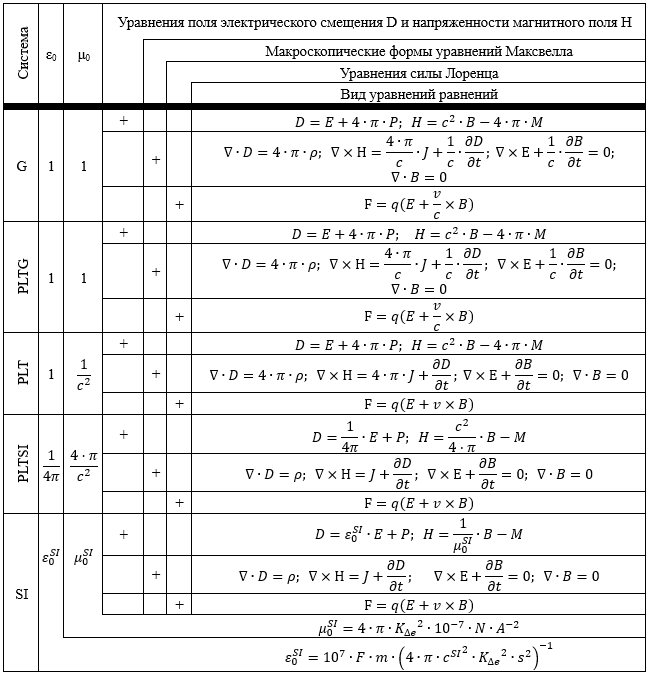
В Таблице 2 приведены уравнения поля электрического смещения D и напряженности магнитного поля H, макроскопические формы уравнений Максвелла и уравнения силы Лоренца в зависимости от значений  ,  и констант рационализации, приведенных в Таблице 1 с учетом соотношений [12]

Таблица 2.

Значения

Классификация основных констант

Важно отметить, что если для SI определяющими константами являются частота перехода сверхтонкого расщепления Cs-133  , скорость света в вакууме, постоянная Планка, элементарный заряд e и постоянная Больцмана (другие определяющие константы SI вне предметного поля настоящей статьи), для G частота перехода сверхтонкого расщепления Cs-133  , скорость света в вакууме, постоянная Планка, постоянная тонкой структуры и постоянная Больцмана, то для PLT, PLTSI и PLTG – планковская длина и скорость света.

Согласно классификации [8] основные единицы и физические постоянные можно отнести к одному из трех классов: безразмерные постоянные (А), независимые размерные постоянные (С), производные (все оставшиеся) размерные постоянные (В). Т.е. имеет место отношение (постоянная класса В) = (постоянная или комбинация постоянных класса А) х (постоянная или комбинация постоянных класса С).

В Таблице 3 представлена классификация основных постоянных и единиц измерения, представленных в статье систем единиц.

Таблица 3

Классификация основных постоянных и единиц измерения

Роль скорости света в определении основных констант

В статье [7] автор предложил обсуждение фундаментальных физических констант начать с несколько неожиданного вопроса: «что изменилось бы в окружающем нас мире, если бы скорость света была иной, чем на самом деле, скажем, на десять порядков большей т.е. 3·10²⁰см/с?». И полагая при этом неизменными значения Постоянной планка, элементарного электрического заряда, массы электрона и протона и проанализировав уравнения связи фундаментальных взаимодействий приходит к выводу, что как при увеличении скорости света, так и при ее уменьшении мир изменился бы радикально и многие физические процессы и тем более жизнь в нем была бы невозможна.

Но давайте включимся в эту «игру» с позиции систем PLT, PLTSI и PLTG.  Начнем с того, что постоянная Планка, при увеличении скорости света на порядок, увеличится на 3 порядка (обозначения изменённых значений в SI пометим точкой):

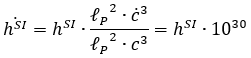
Планковская масса и планковский заряд и, соответственно, масса элементарных частиц и элементарный заряд, эффективный заряд слабого взаимодействия для протона и эффективные заряды прочих взаимодействий – на 2 порядка

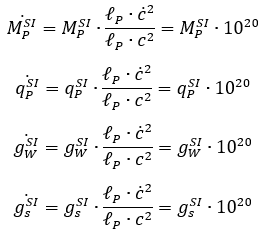
Постоянная Ферми – на 40 порядков

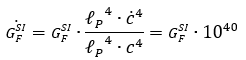
но при этом, в силу приведенного выше масштабирования, не изменятся безразмерные константы взаимодействий , как квадрат отношения эффективных зарядов к планковскому заряду, а также константа слабого взаимодействия (в частности, для протона)

и планковская температура

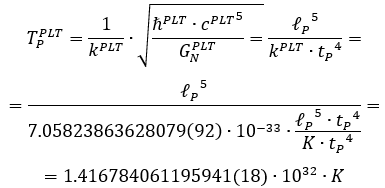
Не изменятся константы, имеющие размерность пространственной протяженности, как инвариантные к скорости света:

постоянная Ридберга:

томсоновское сечение рассеяния фотонов свободными электронами:

рэлеевское нерезонансное рассеяние света атомами:

Боровский радиус:

Этот перечень можно продолжать, главное – сохранятся отношения зарядов и масс элементарных частиц и уравнения связи продолжат работать. Изменятся частоты при сохранении спектральных полос, изменятся энергии взаимодействий.

Для полноты картины посмотрим на этот мир глазами метролога. Поскольку постоянная Ридберга не зависит от скорости света длина волны для частоты перехода сверхтонкого расщепления Cs 133 не изменится, но частота  будет на 10 порядков выше. То есть наш метролог определит 1 секунду согласно известной формуле [5]:

Длину в один метр он определит , т.е. .

Массу в один kg он определит по известной формуле

Соответственно ()

Заряд в один кулон

Таким образом, изменятся все определяющие константы и единицы измерений кроме единиц длины.

Но с точки зрения метрологии все эти величины останутся неизменными, как и уравнения связи законов физики, т.е. даже учебники переписывать не придется.

В концепции переменной скорости света (ПСС или VSL) считается, что с в некоторых случаях может не быть константой. В частности, автор [13] полагает, что после Большого взрыва перед фазовым переходом от газа кварков к нуклонам свет распространялся более чем на 32 порядка быстрее сегодняшнего значения, что позволяет решить проблему горизонта и ряд других проблем. Но успех дальнейшего развития теории автор связывает с выбором системы единиц, в которой изменение других констант было бы связано с изменяющейся скоростью света. Системы единиц PLT, PLTSI, PLTG – возможные кандидаты на эту роль.

Роль Планковского заряда в определении констант взаимодействия

Вернемся к нашему миру и скорости света.

Все безразмерные константы взаимодействий определяются отношением эффективного заряда частиц, участвующих во взаимодействии, к произведению . Ниже приведены эти же отношения в системе PLT:

Гравитационного:

Электромагнитного:

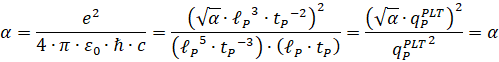
Сильного взаимодействия на уровне адронов:

Для кварков в квантовой хромодинамике

И даже для слабого взаимодействия, в частности для протона:

Таким образом допустимо предположить, что величина эффективного заряда по отношению к планковскому и определяет константу взаимодействия.

Величина планковского заряда любой природы имеет значение , т.е. для эффективных зарядов допустима модель, связанная с пространственно-временным процессом с предельной скоростью течения равной скорости света в вакууме.

Для того, чтобы такие процессы, имеющие одинаковую размерность, отличались качественно пространство с ними связанное должно отличатся хотя бы одним ортогональным измерением. То есть PLT косвенно указывает на наличие в метрике нашего пространства скрытых измерений. Тогда возможно формирование многомерной модели процесса, эквивалентного истинно элементарной частице, из которой, по соображениям размерности, можно выделить фрагмент, эквивалентный эффективному заряду размерности соответствующего взаимодействия. Энергия частицы, имеющей массу покоя, связана с частотой волны де Бройля соотношением [9], где  трактуется также, как частота вращения амплитуды вероятности. Но частота,  может быть и частотой протекания многомерного процесса, эквивалентного истинно элементарной частице. Вероятно, такой подход может быть применим, как к не имеющим массу покоя частицам, таким как фотон

  , так и к частицам, имеющим массу покоя

 ,

где  – планковская угловая частота.

Известна зависимость констант фундаментальных взаимодействий от энергии взаимодействия и сближения их значений при приближении к планковским энергиям [9]. Но с учетом вышеизложенного допустимо предположить, что изменения эффективных зарядов связаны с топологией соответствующего пространства и релятивистской деформацией области локализации частицы, и соответственно, изменением параметров эквивалентного многомерного процесса. То есть изменяются не константы взаимодействия, а величины эффективных зарядов.

Не исключено, что система PLT применима и для решения одной из десяти Проблем Стандартной Модели – поиске структуры фундаментальных частиц.

Выводы

1.  Планковская LT система единиц, построенная на основе кинематической системы единиц Р.О. ди Бартини является полноценной системой единиц и в любом из трех представленных вариантов (PLT, PLTSI, PLTG) может быть использована для производства научных и инженерно-технических расчетов с применением приведенных в статье форм основных уравнений.

2. Представленные переводные коэффициенты между PLT и SI, PLT и Гауссовой системой, а также уточненные переводные коэффициенты между электромагнитными величинами SI и Гауссовой системой позволяют исходные данные и результаты расчетов, полученных в одной системе, использовать в другой без потери точности вычислений.

3. Постоянная Планка в системах PLT, PLTSI, PLTG является не фундаментальной, а производной константой.

4. Переводной коэффициент значения массы между системами PLT, PLTSI, PLTG и SI и Гауссовой системой эквивалентен гравитационной постоянной Ньютона, то есть допустимо применение полученного не экспериментальным путем значения гравитационной постоянной Ньютона в значении