ДИСКРЕТНЫЕ И НЕПРЕРЫВНЫЕ МОДЕЛИ МНОГОПЕРИОДНОГО ПЛАНИРОВАНИЯ ПРОИЗВОДСТВА БЕНЗИНОВ

DISCRETE AND CONTINUOUS MODELS OF MULTI-PERIOD GASOLINE PRODUCTION SCHEDULING

Sergey Gorbunov

Supervisor, MCE-Engineering LLC, Russia, Moscow

Aleksandr Egorov

Doctor of Technical Sciences, Professor, D.I. Mendeleev Russian University of Chemical Technology, Russia, Moscow

Valery Sidorov

Candidate of Technical Sciences, Professor, I.M. Gubkin Russian State University of Oil and Gas (RGU), Russia, Moscow

Аннотация. В статье рассматривается алгоритм планирования многопериодного расписания непрерывного приготовления бензинов во времени с использованием математических моделей с линейными и нелинейными характеристиками процессов смешения (MPIP-C algorithm multi-period, inventory pinch-based algorithm with continuous-time) [3]. MPIP-C декомпозирует проблему планирования на: приближенное и детальное планирование.

В работе используются нелинейные ограничения для давления паров по Рейду (RVP), октанового числа по исследовательскому (RON) и октанового числа по моторному методам (MON).

Abstract. The paper considers an algorithm for generating a multiperiod schedule of continuous fuel preparation in time for mathematical models with linear and nonlinear characteristics of blending processes (MPIP-C algorithm - multi-period, inventory pinch-based algorithm with continuous-time [3] model). MPIP-C decomposes the scheduling problem into: approximate and detailed scheduling. Nonlinear constraints are used for the Reid vapor pressure (RVP), Research Octane Number (RON) and Motor Octane Number (MON) in this paper.

Ключевые слова: алгоритм, многопериодное планирование, нелинейные модели смешивания, рецептура смеси бензинов.

Keywords: algorithm, multiperiod schedule, nonlinear blend models, gasoline blend formulation.

Введение

Для решения задач планирования производства бензинов, состоящих из цепочек последовательных операций: закупка и хранение сырья, процессов переработки сырья в промежуточную и товарную продукцию, хранение и распределение по складам и конечным потребителям, разрабатывается математическая модель и формулируется задача оптимального планирования.

В целях наилучшего управления всей структурой цепи поставок (по критерию максимизации прибыли или минимизации затрат) предполагается принятие решений на разных уровнях данного процесса.

Результатом являются наилучшие последовательности операций и условия работы для достижения целевых показателей с учетом ограничений на запасы и планы производства.

Планирование производства

Планирование осуществляется на меньших временных горизонтах (например, дни или недели) и включает в себя больше операционных правил и ограничений.

Модели планирования производства строятся путем разбиения временного горизонта на ряд периодов, длительность которых обычно устанавливается равной некоторой календарной единице (например, месячные или квартальные периоды). Такой подход приводит к моделям, размерность которых растет линейно с увеличением числа периодов. Если модели нелинейные, то вероятность столкнуться с проблемами сходства решений значительно возрастает с увеличением размерности задачи.

Процессы, протекающие на технологических установках, являются нелинейными, но обычная практика составления расписаний заключается в аппроксимации поведения системы линейными моделями [4, с. 1001], [6, с 9156]. Последние достижения сделали возможным использование нелинейных моделей для решения некоторых задач составления расписаний [5, с. 122].

Алгоритм MPIP-C позволяет использовать нелинейные модели для решения задач планирования и составления расписания для работы нефтеперерабатывающих заводов, которые производят несколько продуктов путем переключения с производства одного продукта на другой. Примером такой системы является смешение бензинов. Алгоритм MPIP-C использует двухуровневый подход, основанный на инвентаризации, для решения задачи приближенного планирования [2, с. 3748] на основе нелинейных моделей смешения бензинов:

• вычисление приближенного расписания на основе нелинейной модели смешения бензинов, исходя из существующего минимального количества оптимальных рецептур смешения на горизонте планирования;
• минимизация общего количества вовлекаемых компонентов смеси;
• распределение резервуаров компонентов для подачи на станцию смешения.

Стратегия декомпозиции

Благодаря долгосрочному плану можно определить, какое сырье должно быть переработано, какие продукты произведены и каково соответственно общее количество для каждого из компонентов.

Результаты долгосрочного плана используются для оптимизации краткосрочной дискретно-временной многопериодной модели приближенного планирования (например, на тридцать дней), которая, в свою очередь, обеспечивает ограничения для модели непрерывного планирования.

Приблизительное планирование

Целью приблизительного составления плана является минимизация производственных затрат или максимизация прибыли.  Сначала определяются объемы производства каждого продукта в каждый период времени и управление продуктовыми резервуарами. После чего для каждой производственной линии задается ограничение минимального производства.  

Приблизительное планирование определяет профиль производства и запасов, который могут быть осуществлены только на границе периода (например, в конце каждого дня).

Детальное планирование

Модель детального планирования допускает выполнение лишь одной задачи в какой-нибудь производственной единице в любой момент времени, гарантируя тем самым выполнимое решение на всем горизонте планирования. Его целевая функция на уровне расписания включает в себя только затраты на переключение и в общем случае расходы на переход от одного режима работы к другому.

При использовании ограничений, накладываемых приблизительным уровнем планирования, детальный уровень составления плана решается гораздо быстрее. Однако из-за последующего сокращения множества выполнимых решений оптимальность вычисленного расписания по отношению к исходной задаче (т. е. без ограничений со стороны приближенного уровня планирования) не гарантируется, хотя ожидается, что разрыв оптимальности будет очень мал.

Один из способов улучшить данное решение – использовать его в качестве исходной точки для модели планирования, включающей ограничения на качество и позволяющей рецептам смеси отличаться от тех, что были рассчитаны ранее на уровне краткосрочного планирования.

Математические модели

В статье приведены только нелинейные уравнения для давления паров Рейда (RVP), октановых чисел (RON, MON), используемых в данной работе.  

Модель 1-го уровня (дискретно-временная ЛП или НЛП)

На 1-м уровне определяются оптимальные рецептуры смеси, которые будут зафиксированы на следующих этапах. Целевая функция минимизирует стоимость смеси и стоимость, связанную с факторами простоя. Переменные простоя включаются в остатки запасов, а их штрафные коэффициенты в целевой функции превышают коэффициенты стоимости компонентов смеси. Поэтому, если задача имеет физически выполнимое решение, переменные простоя будут равны нулю.

Если задача не имеет физически осуществимого решения, то по математической модели определяется численно осуществимое решение с некоторыми ненулевыми переменными простоя. Значения производительности смешивания, предложения компонентов и спроса на продукт являются соответствующими агрегированными значениями для каждого из периодов 1-го уровня. Кроме того, отдельные резервуары с продуктами объединяются в пулы продуктов, а отдельные смесители в один пул.

Решением модели первого уровня является показатель нижней границы глобальной стоимости оптимизации смешивания в каждый соответствующий цикл 1-го этапа и является минимальным количеством, необходимым для удовлетворения спроса.

Ниже представлены нелинейные ограничения на показатели качества. Уравнения (1) и (2) определяют рецептуры смешивания. Система уравнений (3) сформулирована на основе нелинейного правила соединения, [1, с. 28–36].  Система ограничений (4) представляет собой спецификации показателей качества продукта RON, MON и RVP.

Результатом решения задачи оптимизации рецептур смешения по математической модели является вектор компонентов массовых (объемных) долей смешения X.

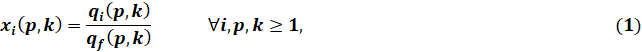
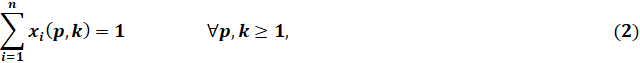
где x_i – массовая (объемная) доля i-го компонента; q_i – массовый (объемный) расход i-го потока компонента смешения; q_f – массовый расход смеси, удовлетворяющий материальному балансу; K={k} – временные периоды модели 1-го уровня (L1-периоды); P={p} – продукты; I={i} – компоненты смеси продукта.

Нелинейная часть модели:

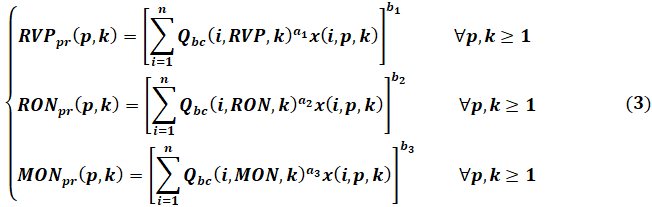
Ограничения по спецификации нелинейной части модели:

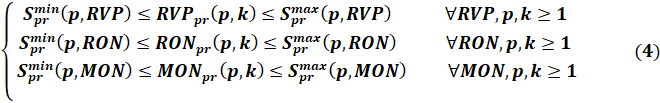
Дискретно-временная модель 2-го уровня

Модель смешанного целочисленного линейного программирования (MILP – mixed integer linear programming). MILP включает в себя: оптимизацию рецептур смеси и эксплуатационные характеристики, такие как параллельные неидентичные блендеры и их производительность, многоцелевые резервуары, планы по поставкам.

На втором уровне формируются планы смешивания, доставки продукта и схемы обслуживания резервуаров. Результатом планирования смешивания компонентов бензина является рецептура смеси, смеситель (блендер) и период соединения. План отгрузки определяет объем продукта из отдельного резервуара для каждого заказа за минимальный период времени.

Модель решается в два этапа, определяются: выполнимость рецептур смеси; оптимизация процесса смешения по критерию минимальных переключений, обеспечивающих оперативность обнаружения неэффективности запасов компонентов.

Модель 2-го уровня для проверки выполнимости рецептур смешения имеет переменные в остатках запасов, ухудшающих критерий эффективности рецептур соединения бензинов. Целью данного процесса является минимизация таких переменных. При выполнимости рецептур смешения бензинов на 1-м уровне, такие переменные в запасах по компонентам на 2-м этапе не влияют на решение задачи, в противном случае ухудшенные переменных запасов покажут, какие продукты, в каком количестве и в какие периоды 2-го уровня не могут быть произведены в требуемых объемах.

Непрерывная по времени модель 3-го уровня

На этой ступени определяются: время начала и окончания всех заданий; последовательность работы блендеров; нормы смешивания в каждом цикле соединения; последовательность отгрузки из продуктовых резервуаров и оценка ее стоимости для каждого продукта.

Рецептуры смесей с 1-го уровня, распределение резервуаров, планы доставки и смешения со второго уровня четко фиксируются. Использование информации со 2-го уровня уменьшает пространство поиска и размерность модели на 3-м уровне.

Модель 3-го уровня включает в себя переменные простоя в балансе запасов и ограничения спроса.  

Выводы

В статье используется алгоритм MPIP-C для составления расписания многоцелевых систем, таких как операции смешения на нефтеперерабатывающих заводах. Алгоритм планирования MPIP-C декомпозирует задачу на три различных уровня принятия решений.

Используя информацию, получаемую с верхних уровней, можно составить качественное расписание с минимальным временем выполнения.

  На 1-м уровне используется агрегированное представление системы, т.е. все блендеры рассматриваются в качестве единовременной производственной мощности, производство и спрос одновременно распределяются по временным периодам. Рецептуры смесей, рассчитанные на первом уровне, используются на втором для расчета оптимального плана производства, который включает в себя распределение запасов и привязку поставок продукта к конкретным резервуарам.

Составление расписания прогонов смеси осуществляется на третьем уровне с помощью непрерывной по времени MILP-модели. Решение, получаемое от верхних уровней,  предоставляет дополнительную информацию, которая позволяет уменьшить размерность модели и время вычислений для решения задач 3-го этапа.

Обозначения:

• MPIP-C - multi-period, inventory pinch-based algorithm with continuous-time model (многопериодный алгоритм формирования расписания непрерывного приготовления топлива);
• MILP – mixed integer linear programming (модель смешанного целочисленного линейного программирования). MILP включает оптимизацию рецептур смеси и эксплуатационные характеристики, такие как параллельные неидентичные блендеры и их производительность, многоцелевые резервуары, планы по поставкам.
• MINLP – a discrete-time mixed integer nonlinear programming (дискретная по времени модель смешанного целочисленного нелинейного программирования) для решения задач с ограничениями на запасы, потоки и показатели качества.