РЕЗОНАНСНЫЕ КОЛЕБАНИЯ БУРОВОЙ ШТАНГИ

RESONANT VIBRATIONS OF DRILLING ROD

Akzhan Turdakyn

Master's degree, Kazakh National University Named for Al-Farabi, Kazakhstan, Almaty

Аннотация. Исследуются нелинейные колебания бурильной колонны. Рассмотрена модель горизонтальных колебаний бурильной колонны. С помощью метода гармонического баланса получена амплитудно-частотная характеристика. Исследован резонансный режим колебаний бурильной колонны по основной частоте. Проведен численный анализ и рассмотрено влияние параметров на резонансные колебания.

Abstract. Nonlinear vibrations of the drill rod are investigated. A model of horizontal vibrations of a drill rod is considered. Using the harmonic equilibrium method, an amplitude-frequency response is obtained. The resonant oscillation mode of the drill string at the fundamental frequency is investigated. A quantitative analysis was carried out and the influence of parameters on resonant vibrations was considered.

Ключевые слова: резонанс, буровая штанга, колебания буровой штанги, амплитудно-частотная характеристика.

Keywords: resonance, drilling rod, vibrations of the drilling rod, amplitude-frequency response.

Резонанс-явление резкого увеличения амплитуды вынужденных колебаний системы. Резонанс возникает, когда частота внешнего фактора приближается к определенным значениям, т. е. к резонансным частотам, в зависимости от свойств той или иной системы. В частности, причиной резонанса является совпадение внешней частоты с внутренней частотой колебательной системы.

Резонанс встречается во многих областях, а именно в механике, электронике, оптике, акустике, астрофизике.

Первые наблюдения, которые привели к появлению слова Резонанс, это были знакомые нам звуки. Если мы рассмотрим музыкальные инструменты, например, пианино или другой музыкальный инструмент, в котором бьется нота, а другой предмет это может быть стена, будь то музыкальный инструмент, который продолжает звучать даже после того, как исходный источник звука отключен. Кроме того, вибрируя свободно движущуюся механическую систему на любой частоте, можно вызвать резонанс. Если остановиться на общем определении резонанса, то это состояние движения, которое происходит при совпадении частот естественного и вынужденного типа [1].

В общем случае, нелинейная динамическая модель, описывающая поперечные колебания буровой штанги в плоскостях Oxz и Oyz, вращающейся с частотой ,  под действием продольной сжимающей силы  и крутящего момента  при конечных деформациях описывается системой уравнений [3]

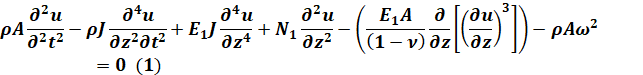
В модели представлены  пространственные колебания бурильной колонны, остальные параметры представляют технические характеристики бурильной колонны.

Сила продольного сжатия меняется со временем и выражается как:

Первоначально считается,что буровые стержни имеют отклонения от прямолинейной формы , которые аппроксимируются спектром форм изгиба. Начальные изгибы возникают из-за соединения бурильной колонны и других факторов [2]:

в виде линейная модель должна быть приведена к типу, удобному для численного интегрирования, из-за сложности прямого интегрирования. Для этого используем метод разбиения переменных т. е. метод Бубнова-Галеркина. В методе Бубнова-Галеркина форма изгиба оси бурильной трубы задается спектром гармонических форм [4].

По методу Бубнова-Галеркина решение системы (1)   дается следующим образом:

                                                                                              (2)

Для получения общей картины колебательного процесса рассматриваются пространственные колебания бурового стержня по основной частоте. Для , поместив функцию (2) в уравнение движения (1), по методу Бубнова-Галеркина для выполнения условия ортогональности по отношению к базисной функции, система с распределенными параметрами была приведена к простому нелинейному дифференциальному уравнению второго порядка по отношению к новой функции .

Коэффициенты:

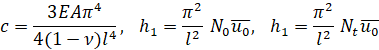
Для рассмотрения резонансных колебаний бурильной колонны введем безразмерную величину и приведем уравнение (3) в безразмерный вид. Где -удельная частота колебаний.

Уравнение (3), приведенное к безразмерному виду, имеет вид

                                                       (4)

где,  ,   

Изучение резонансных режимов движения бурильной колонны сводится к анализу амплитудно-частотных характеристик поперечных колебаний колонны. При рассмотрении периодического решения с периодом, кратным внешней силе, используется обычный метод классификации уравнения в ряд Фурье с неопределенными коэффициентами [3]:

                          (1.5)

Метод гармонического баланса может быть определен путем учета конечных и, как правило, меньших членов. Успех применения этого метода и возникшая ошибка зависят от правильного выбора членов классификации, учитываемых в решении [3].

При рассмотрении основного резонанса уравнений колебаний достаточно аппроксимировать решение простой гармоникой на частоте, равной частоте внешней отклоняющейся силы:

                                                                                               (5)

Используем метод гармонического баланса.

,  

Ставим в уравнение (1.5)

Используя тригонометрические операции, путем отдельной записи коэффициентов функций , получается система уравнений.

Используя метод гармонического баланса, были получены следующие амплитудно-частотные характеристики:

допуская относительное положение к неизвестному , можно найти АЧХ по основной частоте.

Пакет символьных вычислений Wolfram Mathematica был проведен количественный анализ резонанса по основной частоте колебательного процесса вращающейся бурильной колонны. Исследовав влияние длины колонны, начального наклона, продольной сжимающей нагрузки на режимы резонансных колебаний, была построена АЧХ.

На рисунке 1 показаны резонансные кривые дюралюминиевого бурового столба со скоростью вращения ω=5 об/мин, значения продольной нагрузки наружных  и внутренних  диаметров стержня , и исходные величины кривизны  соответственно сечение рассматривается.

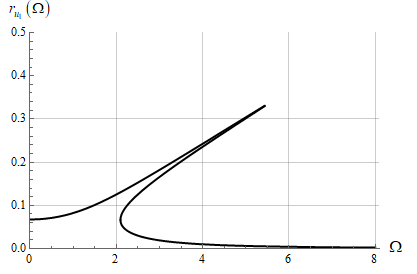
Рисунок 1. АЧХ   резонанса по основной частоте дюралюминиевой буровой штанги

Все резонансные кривые вытянуты вправо, что связано с тем, что модель колебаний бурильной колонны геометрически нелинейна.

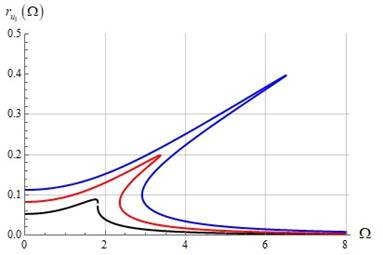
Рисунок 2. Влияние начального значения кривизны на основную резонансную частоту штанги

___ , ___  ,

___

На рис.2 изучено влияние величины начальной кривизны бурильной колонны на ее резонансный режим. Чем более наклонен столбец вначале, тем больше он подвержен колебаниям, и резонанс в системе может возникать в большом диапазоне частот внешнего воздействия, а также расширяется зона неработающей частоты (рис.2).

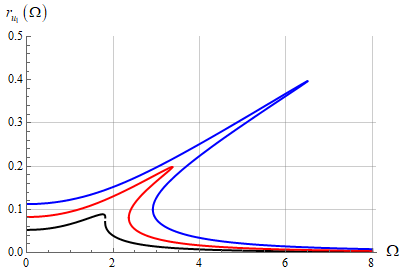
Рисунок 3. Влияние продольной нагрузки на основной частотный резонанс

___, ___, ___     

Проведен анализ влияния внешней сжимающей нагрузки на резонансные кривые. Было обнаружено, что увеличение переменной составляющей внешней нагрузки приводит к увеличению амплитуды колебаний и смещению области резонансных частот бурового стержня в область больших частот (рис.3).

ЗАКЛЮЧЕНИЕ

В прикладной программе Wolfram Mathematica проводились сравнения путем ввода различных параметров изменения амплитуд колебаний колонного трубопровода. Пакет символьных вычислений Wolfram Mathematica был проведен количественный анализ резонанса по основной частоте колебательного процесса вращающейся бурильной колонны. Исследовав влияние длины колонны, начального наклона, продольной сжимающей нагрузки на режимы резонансных колебаний, была построена АЧХ.