РЕШЕНИЕ ПРОБЛЕМЫ КАНТЕЛЛИ ДЛЯ ТАБЛИЧНЫХ ФУНКЦИИ
Конференция: LXXIII Международная научно-практическая конференция «Научный форум: технические и физико-математические науки»
Секция: Теория вероятностей и математическая статистика

LXXIII Международная научно-практическая конференция «Научный форум: технические и физико-математические науки»
РЕШЕНИЕ ПРОБЛЕМЫ КАНТЕЛЛИ ДЛЯ ТАБЛИЧНЫХ ФУНКЦИИ
KANTELLI`S PROBLEM SOLUTION FOR TABULAR FUNCTIONS
Vladislav Ivanchenko
Student, Belorussian state university informatics and radioelectronics, Belarus, Minsk
Vladislav Yakuba
Student, Belorussian state university informatics and radioelectronics, Belarus, Minsk
Irina Bazhenova
Scientific director, Ph. D. phys.-math. sciences, associate professor, Belorussian state university informatics and radioelectronics, Belarus, Minsk
Аннотация. Теория вероятностей является чрезвычайно важным разделом не только математики, но и важным математическим аппаратом в радиотехнике, связи, ядерной, квантовой и молекулярной физике, метрологии и многих других дисциплинах. В данной статье показаны результаты решения проблемы Кантелли для табличных функции, с использованием программирования на языке С++. В результате решения было выявлено подтверждение гипотезы для табличных функции.
Abstract. Probability theory is an extremely important section not only of mathematics, but also an important mathematical apparatus in radio engineering, communications, nuclear, quantum and molecular physics, metrology and many other disciplines. This article shows the results of solving Cantelli's problem for table functions using C++ programming. As a result of the solution, confirmation of the hypothesis for tabular functions was revealed.
Ключевые слова: теория вероятностей, математическая статистика, высшая математика, общая физика, молекулярная физика, квантовая физика, статистическая физика, ядерная физика, физика элементарных частиц, радиотехника, связь, метрология, проблема Кантелли.
Keywords: probability theory, math statistics, higher mathematics, common physics, molecular physics, quantum physics, statistic physics, nuclear physics, particle physics, radio engineering, communications, metrology, Cantelli`s problem.
Проблема Кантелли является одной из открытых проблем в теории вероятностей. Сама проблема представляет из себя следующие условия: есть две случайные независимые друг от друга величины Х и Y, они подчиняются нормальному распределению N(0;1), f(x) является измеримой неотрицательной функцией, а выражение X+f(X)*Y тоже имеет нормальное распределение. Является ли функция почти всюду однозначной? [1]
В статье представлен вариант решения этой проблемы, написанный соавторами на языке С++. Блок-схема решения для одной функции показана на рисунке 1. Так как функции должны быть измеримыми и неотрицательными, то не все табличные функции подходят для такого исследования. В данной статье рассматриваются следующие функции: x2, 2x, log2(x), ln(x), ex, |x|, x!, 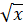 .
.
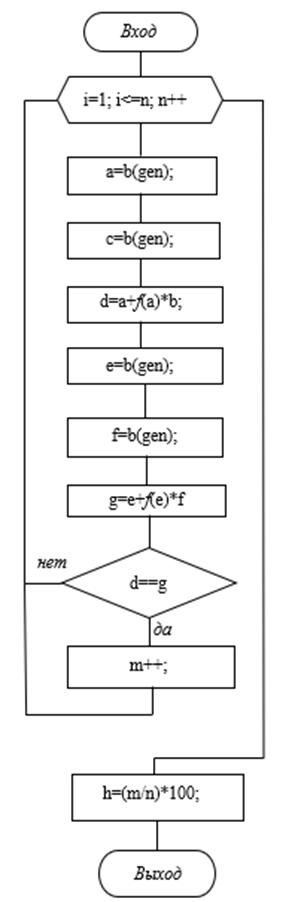
Рисунок 1. Блок-схема цикла для нахождения решения задачи
Сама программа выглядит так:
#include <iostream>
#include <math.h>
#include <ctype.h>
#include <random>
#include <complex>
#include <conio.h>
using namespace std;
int factorial(int cc) {
if (cc < 2)return 1;
return cc * factorial(cc - 1); //Вычисление факториала для функции х!
}
int main() {
long double a, b, c, f, g, h, i, n = 0, j, k, l, m, r, t, o, p, q = 0, w, s, u, y, x, z, aa, ab, ac = 0, ad, ae, af, an = 0, ao, ap, aq, ar, as, at, au, av = 0, aw, ax, ay, az, ba, bb, bc, bd, be, bf = 0, bg, bh, bi, bj, bk, bl, bm, bo, bp, bq=0, br, bs, bt, bw, bz=0, ca=0, cb;
complex <long double> am, al;
long double const E =

int bu, bv, bx, by;
for (h = 1; h <= 1000; h++) { //Проводящий опыт, цикл, где число в неравенстве - количество итерации
random_device rd;
mt19937 gen(rd());
normal_distribution<>d(0.0, 1.0);
long double a = d(gen);
long double b = d(gen); //Генерация случайных величин
c = a + pow(a, 2) * b; //a+f(a)*b
normal_distribution<>c(0.0, 1.0);
long double f = d(gen);
long double g = d(gen);
i = f + pow(f, 2) * g;
normal_distribution<>i(0.0, 1.0);
if (c == i)n++; //Проверка на однозначность в данном опыте
}
j = (n / h) * 100; //Доля событии, где функция однозначна
cout << "x^2 is unambiguous on - " << j << "%" << endl; //Вывод результатов
for (k = 1; k <= 1000; k++) {
random_device pp;
mt19937 gen(pp());
normal_distribution<>d(0.0, 1.0);
long double l = d(gen);
long double m = d(gen);
r = l + fabs(l) * m;
normal_distribution<>r(0.0, 1.0);
long double t = d(gen);
long double o = d(gen);
p = t + fabs(t) * o;
normal_distribution<>p(0.0, 1.0);
if (r == p)q++;
}
w = (q / k) * 100;
cout << "|x| is unambiguous on - " << w << "%" << endl;
for (s = 1; s <= 1000; s++) {
random_device ut;
mt19937 gen(ut());
normal_distribution<>d(0.0, 1.0);
long double u = d(gen);
long double y = d(gen);
aa = u + pow(E, u) * y;
normal_distribution<>aa(0.0, 1.0);
long double x = d(gen);
long double z = d(gen);
ab = x + pow(E, x) * z;
normal_distribution<>ab(0.0, 1.0);
if (aa == ab)ac++;
}
ad = (ac / s) * 100;
cout << "e^x is unambiguous on - " << ad << "%" << endl;
for (ae = 1; ae <= 1000; ae++) {
random_device af;
mt19937 gen(af());
normal_distribution<>d(0.0, 1.0);
complex <long double> ag = d(gen);
complex <long double> ai = d(gen);
am = ag + sqrt(ag) * ai;
normal_distribution<>am(0.0, 1.0);
complex <long double> aj = d(gen);
complex <long double> ak = d(gen);
al = aj + sqrt(aj) * ak;
normal_distribution<>al(0.0, 1.0);
if (al == am)an++;
}
ao = (an / ae) * 100;
cout << "x^(1/2) is unambiguous on - " << ao << "%" << endl;
for (j = 1; j <= 1000; j++) {
random_device k;
mt19937 gen(k());
normal_distribution<>d(0.0, 1.0);
long double ap = d(gen);
long double aq = d(gen);
ar = ap + log(ap) * aq;
normal_distribution<>ar(0.0, 1.0);
long double as = d(gen);
long double at = d(gen);
au = as + log(as) * at;
normal_distribution<>au(0.0, 1.0);
if (ar == au)av++;
}
aw = (av / j) * 100;
cout << "ln(x) is unambiguous on - " << aw << "%" << endl;
for (ax = 1; ax <= 1000; ax++) {
random_device ay;
mt19937 gen(ay());
normal_distribution<>d(0.0, 1.0);
long double az = d(gen);
long double ba = d(gen);
bb = az + pow(2, ba) * ba;
normal_distribution<>bb(0.0, 1.0);
long double bc = d(gen);
long double bd = d(gen);
be = bc + pow(2, bc) * bd;
normal_distribution<>be(0.0, 1.0);
if (bb == be)bf++;
}
bg = (bf / ax) * 100;
cout << "2^x is unambiguous on - " << bg << "%" << endl;
for (bh = 1; bh <= 1000; bh++) {
random_device bi;
mt19937 gen(bi());
normal_distribution<>d(0.0, 1.0);
long double bj = d(gen);
long double bk = d(gen);
bl = bj + (log(bj)/log(2)) * bk;
normal_distribution<>bl(0.0, 1.0);
long double bm = d(gen);
long double bo = d(gen);
bp = bm + (log(bm)/log(2)) * bo;
normal_distribution<>bp(0.0, 1.0);
if (bl == bp)bq++;
}
br = (bq / bh) * 100;
cout << "log2(x) is unambiguous on - " << br << "%" << endl;
for (bs = 1; bs <= 1000; bs++) {
random_device bt;
mt19937 gen(bt());
normal_distribution<>d(0.0, 1.0);
int bu = d(gen);
int bv = d(gen);
bw = bu + factorial(bu) * bv;
normal_distribution<>bw(0.0, 1.0);
int bx = d(gen);
int by = d(gen);
bz = bx + factorial(bx) * by;
normal_distribution<>bz(0.0, 1.0);
if (bw == bz)ca++;
}
cb = (ca / bs) * 100;
cout << "x! is unambiguous on - " << cb << "%" << endl;
return 0;
}
Результаты работы программы представлены на рисунках 2 – 5:
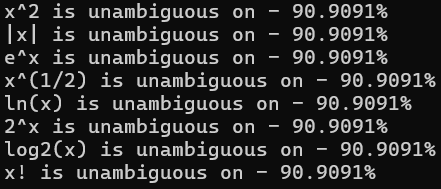
Рисунок 2. Результаты работы программы при 10 итерациях

Рисунок 3. Результаты работы программы при 100 итерациях
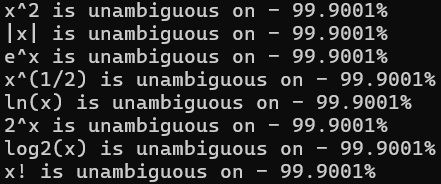
Рисунок 4. Результаты работы программы при 1000 итерациях

Рисунок 5. Результаты работы программы при 10000 итерациях
В результате можно сказать, что, при вышеперечисленных условиях, функции, по крайней мере те, которые рассматриваются в данной статье, почти всюду однозначны. Это может использоваться в математике, статистике, физике и других дисциплинах как математический аппарат.


