ОПРЕДЕЛЕНИЕ ВЕЛИЧИНЫ КОЭФФИЦИЕНТА ИЗБЫТКА ВОЗДУХА ДЛЯ ЗАДАННОЙ МАКСИМАЛЬНОЙ ТЕМПЕРАТУРЫ РАБОЧЕГО ТЕЛА В МОДЕЛИ РАБОЧЕГО ЦИКЛА ДИЗЕЛЯ

DETERMINATION OF A VALUE OF THE AIR EXCESS COEFFICIENT FOR A GIVEN WORKING FLUID MAXIMUM TEMPERATURE IN THE DIESEL ENGINE OPERATING CYCLE MODEL

Alexei Stefanovsky

Candidate of Science, Associate Professor, Melitopol State University, Russia, Melitopol

Аннотация. В рамках классического теплового расчёта дизеля предложен способ определения величины коэффициента избытка воздуха, при которой достигается заданная максимальная температура рабочего тела. Использование этого способа пояснено на основе опубликованных индикаторных диаграмм рабочих циклов дизелей.

Abstract. Within the framework of the classical thermal calculation of a diesel engine, a method is proposed for determining the value of the air excess coefficient at which a given maximum temperature of the working fluid is reached. Using this method is explained on the basis of published indicator diagrams of diesel engine operating cycles.

Ключевые слова: коэффициент избытка воздуха, максимальная температура рабочего тела, рабочий цикл, дизель.

Keywords: air excess coefficient, maximum temperature of the working fluid, operating cycle, diesel engine.

Наряду с максимальным давлением рабочего тела p_max в цикле дизеля, важным показателем служит и максимальная температура рабочего тела T_max, усреднённая по объёму последнего. Согласно Лазареву [6, с. 83], от уровня p_max зависит механическая напряжённость (в том числе «жёсткость» сгорания), а от уровня Т_max – тепловая напряжённость работы дизеля. Можно представить, что исходя из допустимой тепловой напряжённости ответственных деталей последнего, будет задана величина Т_max.

В классическом тепловом расчёте (ТР) дизеля максимальная температура рабочего тела T_z – термодинамический аналог температуры T_max – находится как один из двух корней квадратного уравнения [5, с. 78; 9, с. 35]

a_zT_z² +b_zT_z –c_z = 0,                                                                                                    (1)

где a_z и b_z – коэффициенты, зависящие от коэффициента избытка воздуха (КИВ) α_ив и имеющие единицы измерения Дж/(моль*К²) и Дж/(моль*К); c_z – свободный коэффициент (Дж/моль), зависящий также от ряда других факторов:

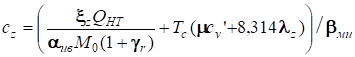,                                                                             (2)

где ξ_z – коэффициент использования теплоты при сгорании (КИТС); λ_z – степень повышения давления при сгорании (СПДС); γ_r – коэффициент остаточных газов;  Q_нт – низшая теплота сгорания топлива, кДж/кг; М₀ – стехиометрическое количество воздуха для полного сгорания топлива, кмоль/кг; T_c – температура рабочего тела в конце сжатия, К (при верхнем положении поршня и отсутствии сгорания); μc_v’ – средняя удельная теплоёмкость свежего заряда, Дж/(моль*К), зависящая от Т_с; β_ми – коэффициент молекулярного изменения, равный

β_ми = 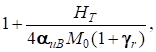                                                                                               (3)

где Н_т – массовое содержание водорода в топливе. Параметры Q_нт и М₀ зависят от Н_т, а также от массового содержания других химических элементов в топливе (С_т, О_т, S_т), причём основное влияние оказывают Н_т и С_т.

Таким образом, кроме α_ив, на T_z влияют параметры ξ_z, γ_r, λ_z, Т_с и свойства дизельного топлива (параметры Q_нт, М₀ и Н_т). В свою очередь, температура сжатого заряда T_c зависит от температуры заряда в конце впуска Т_а, степени сжатия ε и среднего показателя политропы сжатия, a на Т_а влияют коэффициент γ_r и температура Т_r остаточных газов, температура среды во впускных каналах Т_0(к) и увеличение температуры ∆Т_а этой среды при поступлении в цилиндр. Для данных марки дизеля и сорта топлива, параметры ε, Q_нт и М₀ постоянные, а другие параметры (кроме ξ_z, λ_z и α_ив) влияют на T_z незначительно или изменяются слабо. Из трёх параметров, перечисленных в скобках, можно исключить СПДС λ_z, предполагая, что в различных случаях ТР и для реальных дизелей номинальные значения СПДС и КИВ изменяются взаимно-противоположно (то есть, в выборках выполненных ТР и исследованных реальных дизелей при снижении КИВ растёт СПДС и наоборот). Поэтому, в конечном счёте, основную роль играет влияние КИТС и КИВ на расчётную максимальную температуру заряда T_z. Из этих двух параметров изменяемым в большей степени и легко управляемым в дизелях (за счёт изменения цикловой подачи топлива) является КИВ.

Цель работы – предложить соответствующий классическому ТР способ определения величины КИВ, при которой достигается заданная максимальная температура заряда T_z.

Рассмотрим, как выразить КИВ α_ив из исходного уравнения (1), учитывая выражения для коэффициентов a_z и b_z [7 и 8, с. 11; 9, с. 34]:

 a_z = 10⁻³(1,55 +1,38/α_ив); b_z = 28,414 +0,92/α_ив.                                                                 (4а, 4б)

Выражение для свободного коэффициента c_z (2) имеет вид отношения двух функций, линейных относительно обратной величины 1/α_ив, которую можно условно назвать «коэффициентом избытка топлива» и обозначить α_ит:

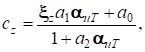                                                                                                       (5)

где а₀ – это второе слагаемое в скобках выражения (2), а коэффициенты а₁ и а₂ взаимосвязаны:

а₁ = 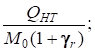а₂ = 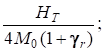 а₁/а₂ = 4Q_нт/Н_т.                                                        (6а, 6б, 6в)

Выражения (4а, 4б) принимают вид

a_z = 10⁻³(1,55 +1,38α_ит); b_z = 28,414 +0,92α_ит,

и с учётом (5) уравнение (1) примет вид

10⁻³(1,55 +1,38α_ит)T_z² +(28,414 +0,92α_ит)T_z = 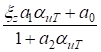.                                                            (7)

Оно приводится к квадратному относительно α_ит:

a_итα_ит² +b_итα_ит +с_ит = 0,(8)

где коэффициенты a_ит, b_ит и с_ит определяются с помощью выражений

a_ит = a₂T_z(0,92 +1,38_*10⁻³T_z);                                                                                         (9a)

b_ит = (1,38 +1,55a₂)10⁻³T_z² +(0,92 +28,414a₂)T_z –ξ_za₁;                                                                 (9б)

с_ит = 1,55_*10⁻³T_z² +28,414T_z –a₀.                                                                                    (9в)

Корни квадратного уравнения (8) определяются выражением

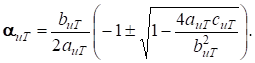                                                                                     (10)

Какой из двух корней правильный (то есть даст величину α_ит, которая согласуется с опытом эксплуатации и моделирования работы дизелей), можно установить, рассмотрев следующий пример.

В работе [2, с. 121] для автомобильного дизеля «Татра-912» (6Ч 11/13) опубликована свёрнутая индикаторная диаграмма (ИД), где изображены линии процессов с рабочим телом в координатах давление – объём и температура – объём (p – V, T – V). При этом максимальные параметры заряда были следующие: давление p_max ≈ p_z = 7,23 МПа (в оригинале выражено в кгс/см², установлено с помощью шкалы давления); температура T_max = 2140 K и T_z = 2080 K (соответственно, согласованная с p_max и найденная с помощью ТР; значения были указаны на поле ИД). Режим работы данного дизеля можно считать номинальным (и по частоте вращения, и по уровню подачи топлива). Так как подробности ТР этого дизеля не были опубликованы, то примем следующие значения параметров: ξ_z = 0,75 (типично для быстроходных автотракторных дизелей); γ_r = 0,03; λ_z ≈ 1,64 (установлена с помощью линий сжатия и сгорания в координатах p – V); Т_с ≈ 950 К (установлена с помощью линии сжатия в координатах Т – V); свойства топлива Q_нт = 42500 кДж/кг; H_T = 0,13; М₀ = 0,495 кмоль/кг (типичны в литературе по теории двигателей внутреннего сгорания). Тогда после подстановки этих значений в формулы (6а), (6б), (9а – 9в) и с учётом (2) получим:

а₀ = 950 (20,16 +0,00174_*950 +8,314_*1,64) ≈ 33676 Дж/моль;

 а₁ = 42500/(0,495_*1,03) ≈ 83358 Дж/моль;

 а₂ = 0,13/(4_*0,495_*1,03) = 0,063744… ≈ 0,064 кг/кмоль;

a_ит = 0,06374_*2080 (0,92 +0,00138_*2080) = 502,560 кг_*кДж/кмоль²;

  b_ит = (1,38 +1,55_*0,06374)10⁻³2080² +(0,92 +28,414_*0,06374) 2080 –

–0,75_*83358 = 6397,89 +5680,94 –62518,5 = –50439,7 Дж/моль;с_ит = (0,00155_*2080 +28,414) 2080 –33976 = 32131 Дж/моль.

Согласно (10), два значения коэффициента избытка топлива α_ит, являющиеся корнями квадратного уравнения (8), определяются из выражения

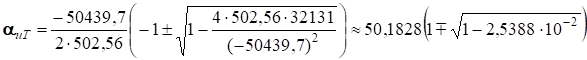
и оба положительные: α_ит = {0,641115; 99,72446}. Им соответствуют два значения КИВ: α_ив = 1/α_ит = {1,55978; 0,0100276}, из которых только первое можно обеспечить в дизеле (речь идёт о суммарном КИВ, а не о локальном). Значит, в (10) правильный знак – это плюс. Последнее выражение можно упростить, учитывая, что для малого числа х, вычитаемого из единицы, (1 –х)^0,5 ≈ 1 –х/2 [1, с. 87 и 132]:

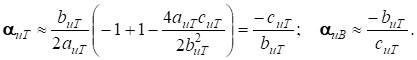                                                                (11а, 11б)

Тогда в рассмотренном примере получится значение КИВ

α_ив = 50439,7/32131 = 1,56981…,

очень близкое к 1,55978 (относительное завышение менее точного результата 0,64%).

Выражения (11б), (9б) и (9в) позволяют кратко охарактеризовать влияние максимальной температуры T_z и КИТС на КИВ. Влияние T_z – сложное, так как в числитель и знаменатель (11б) входит эта температура в 1-й и 2-й степенях. Но влияние КИТС ξ_z на КИВ описывается линейной функцией, так как этот параметр находится только в числителе (11б), согласно (9б). Поэтому чем более высокое значение КИТС задано, тем больше будет числитель (11б) и, следовательно, КИВ для заданной температуры T_z. Так как при увеличении КИВ полнота сгорания и эффективность рабочего цикла дизелей повышаются [3, с. 85; 6, с. 73], то отмеченный характер влияния КИТС на КИВ не противоречит опытным данным.

На величину расчётной максимальной температуры T_z влияет принятый способ вычисления средних теплоёмкостей сред. В приложении учебника [4, с. 369] изображена развёрнутая ИД турбопоршневого дизеля (ε = 12, давление наддува около 0,35 МПа) для КИВ α_ив = 1,9, на которой показано изменение давления и температуры рабочего тела при моделировании цикла упрощённым (классический ТР) и более сложным способами. При этом в первом случае T_z ≈ 1880 К для значений параметров ТР ξ_z = 0,85; γ_r = 0,03; λ_z ≈ 1,78; Т_с ≈ 798 К, a во втором случае максимальная температура T_max ≈ 1785 K. Применение вышеописанного способа вычисления КИВ к этим сведениям дало величину  α_ив ≈ 2,02 (примерно на 6% больше 1,9), а расчёт температуры T_z c использованием выражений (4а), (4б), (3) и (2) дал её величину около 1930 К (на 2,6% выше). Но так как, независимо от принятого в ТР способа вычисления теплоёмкостей сред, получаемая величина расчётной максимальной температуры рабочего тела является довольно грубым приближением – заменой реального поля температуры в объёме цилиндра, то в учебной практике целесообразнее применять более простой способ их вычисления.

Таким образом, определить величину КИВ, при которой достигается заданная максимальная температура рабочего тела T_z (в упрощённой модели рабочего цикла дизеля, которой является классический ТР), можно с помощью формулы (11б), а также ряда связанных с ней формул.