Компьютерное конструирование полимерных композиций с заданными характеристиками

Аннотация. Для решения задач моделирования предлагается алгоритм оценки прочностных свойств армированных полимерных систем, основанный на анализе напряженно-деформированного состояния представительного объема материала.

При решении задач конструирования используется понятие поверхности отклика в пространстве состояний, характеризующей зави­симость конкретной эффективной характеристики от управляющих параметров. Тогда заданному уровню эффективной характеристики на этой поверхности отвечает линия, а заданному интервалу значений – полоса. Проекция этой полосы на плоскость управляющих параметров определяет набор требуемых значений этих параметров в виде полосы.

Ключевые слова: полимерные композиции; механические свойства; матрица-включения.

Постановка задач

Модификация свойств полимерных композиционных материалов (ПКМ), в том числе деформационно-прочностных, достигается путем использований армирующих включений в виде компактных частиц или в виде волокон. Армирующие частицы играют двоякую роль. С одной стороны, они могут повысить прочностные свойства компо­зиции, с другой – являться источниками концентрации напряжений, что может привести к локальному разрушению. Размеры включений, как правило, отличаются от масштаба изделия на несколько порядков. Поэтому при расчете параметров напряженно-деформированного состояния (НДС) изделия задачи обычно решаются в предположении, что материал является однородным, и при анализе можно использовать так называемые эффективные характеристики.

Предлагаемый подход иллюстрируется примером анализа НДС стальной подложки и покрытия триботехнического назначения. Определение параметров НДС проводится на основе соотношений механики деформируемого твердого тела методом конечных элементов [1].

В покрытии выделяются области, где напряжения и/или деформации являются экстремальными. Из наиболее опасных с точки зрения прочности зон «вырезается» область, которая снова подвергается анализу НДС. Масштаб «вырезанной» области выбирается таким образом, чтобы он был соизмерим с размером включений, что позволяет учесть форму, расположение, размер и свойства включений на конечно-элементной сетке [2, 3].

Результаты расчетов получаются в виде детальных распределений параметров НДС с учетом наличия реальных элементов структуры, рис. 1. В итоге получаются не осредненные по объему, а реальные распределения деформаций и напряжений, и прогноз прочности на основе этих распределений становится более корректным и достоверным.

Расчеты показали, что для материала, наполненного включениями компактной формы, максимальные нормальные и касательные напряжения, интенсивности деформаций и напряжений в выделенном элементе покрытия увеличиваются в несколько раз по сравнению с гомогенной средой.

Напряжения, возникающие на границе матрица-включение, значительно больше, чем в выделенном для анализа объеме однород­ного покрытия. Это может привести к возникновению локального разрушения.

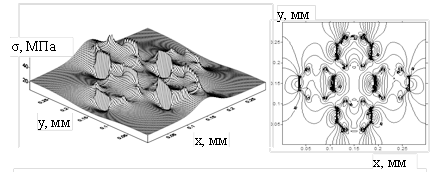
Рисунок 1. Поверхность распределения интенсивностей напряжений при нагружении наполненной полимерной композиции и соответствующие изолинии

Эффективные характеристики материала получаются с исполь­зованием процедур осреднения [6]. Детальные распределения параметров НДС, играющих определяющую роль при оценке прочности с использованием тех или иных критериев, при определении эффективных характеристик заменяются своего рода интегральными значениями параметров НДС, в частности, теми, которые определяют кривую напряжения-деформации.

Для наглядности рассматривается случай, когда используются две управляющие характеристики – степень наполнения и средний радиус компактных включений. В этом случае зависимость любой из перечисленных выше эффективных характеристик от управляющих параметров может быть представлены визуально как поверхность отклика в трехмерном пространстве состояний совершенно аналогично поверхности вида z = z (x, y) в обычном пространстве с использованием декартовых координат. Пример в виде поверхности λ = λ (ρ, φ) приведен на рис. 2, где λ – коэффициент теплопроводности, ρ и φ – управляющие параметры, указанные выше. Аналогичные зависимости можно привести и для других эффективных характеристик.

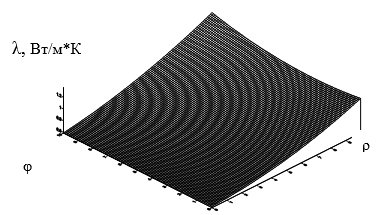
Рисунок 2. Зависимость коэффициента теплопроводности λ от степени наполнения φ (ось ординат) и среднего размера включений ρ (ось абсцисс)

Поскольку речь идет об интервале заданных значений, то на каждом из графиков оставляем полосу, ограниченную двумя изолиниями, отвечающими верхней и нижней границам заданного интервала (рис. 3).

10,2 ÷ 9,8 МПа – предельное напряжение разрушения (жирные линии);

114 ÷ 104 % - предельная деформация разрушения материала (пунктирные линии);

1 ÷ 0,7 Вт/м*К - коэффициент теплопроводности (штрихпунктирные линии);

Чтобы найти управляющие параметры, придающих требуемые значения эффективных характеристик (в виде заданных интервалов), нужно наложить полученные графики в виде изолиний друг на друга.

Рисунок 3. а) изолинии распределения предельного напряжения разрушения при растяжении; б) изолинии распределения предельной деформации разрушения при растяжении; в) изолинии распределения коэффициента теплопроводности

Совмещая графики, получаем нужную область для среднего радиуса включений и степени наполнения композиции, обеспечивающих попадание макрохарактеристик в заданные интервалы.

На рис. 4 полученный неправильный затемненный криволинейный «шестиугольник» и есть область значений, которые необходимы для получения заданных значений эффективных характеристик [7].

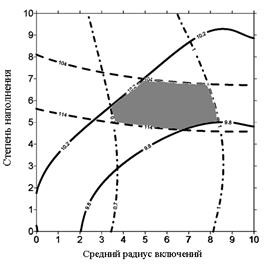
Рисунок 4. Область значений управляющих параметров

С формальной точки зрения любое сочетание управляющих параметров, попадающих в полученную область, дает решение постав­ленной задачи. В то же время, очевидно, что с практической точки зрения следует придерживаться вариантов (точек), наиболее удаленных от границ области. Тогда при случайных отклонениях значений управляющих параметров от номинальных значений, не превосходящих расстояние до границы, результат будет соответствовать прогнози­руемому варианту; в других случаях можно легко выйти за границу области.

Выводы

1. Разработанные и реализованные модели позволяют учитывать физико-механические свойства материала на разных уровнях анализа – от макроуровня, отвечающего детали в целом, до уровня, учиты­вающего наличие надмолекулярных структур в полимерной матрице. Это позволяет получить эффективные характеристики в зависимости от управляющих параметров, определяющих структурные особенности неоднородного материала.

2. Набор моделей представляет собой систему, в которой каждая следующая модель позволяет учитывать в соответствующем масштабе наличие новых структурных элементов, которые на предыдущем уровне либо не принимаются во внимание, либо заменяются средой с осредненными характеристиками.

3. Реализация моделей и анализ получаемых с их исполь­зованием результатов позволяют понять механизмы, приводящие к разрушению композитного материала под нагрузкой, и выработать рекомендации по улучшению деформационно-прочностных макро­характеристик композиции.

4. Решением ряда прямых задач в пространстве состояний получается дискретный набор т.н. опорных точек, по которым можно построить поверхности отклика эффективных свойств материала на значения управляющих параметров. Анализ этих поверхностей делает возможным решение основной задачи компьютерного конструирования материала – получение материала с эффективными физико-механическими характеристиками, попадающими в заданные интервалы.