ТЕОРЕТИЧЕСКОЕ МОДЕЛИРОВАНИЕ РЕКУПЕРАЦИИ ЭНЕРГИИ МАГЛЕВА

THEORETICAL MODELING OF MAGLEVA ENERGY RECOVERY

Kuzmin Dmitry Aleksandrovich

Doctor of Sciences, Professor, Chelyabinsk State University, Russia, Chelyabinsk

Maltsev Ivan Valerievich

Candidate of Sciences, Аssociate Professor, Chelyabinsk State University, Russia, Chelyabinsk

Bychkov Igor Valerievich

Doctor of Sciences, Professor, Chelyabinsk State University, Russia, Chelyabinsk

Аннотация. Представлены результаты теоретического моделирования процесса рекуперации энергии при торможении поезда на магнитной подушке (маглева). Разработана математическая модель, описывающая электромеханические процессы в цикле "разгон-торможение". На основе численного моделирования для поезда массой 50 т на перегоне 5 км оценен коэффициент полезного действия рекуперации за цикл, составивший ~45.5%. Проанализировано влияние типа электромагнитной системы (на обычных и сверхпроводящих магнитах) на энергоэффективность.

Abstract. The article presents the results of theoretical modeling of energy recovery during braking of a magnetic levitation train (maglev). A mathematical model describing the electromechanical processes in the acceleration-deceleration cycle is developed. Based on numerical simulations for a 50-ton train on a 5-km section, the energy recovery efficiency per cycle was estimated at ~45.5%. The impact of the electromagnetic system type (conventional and superconducting magnets) on energy efficiency was analyzed.

Ключевые слова: магнитная левитация, рекуперация энергии, линейный двигатель, энергоэффективность, математическое моделирование.

Keywords: magnetic levitation, energy recovery, linear motor, energy efficiency, mathematical modeling.

Работа выполнена при поддержке гранта в виде областной субсидии автономным и бюджетным учреждениям на создание региональных молодежных лабораторий, предусмотренной постановлением Правительства Челябинской области от 20.11.20224 г. № 657-П.

1. Введение.

Развитие высокоскоростного транспорта на магнитной подушке (маглева) является одним из приоритетных направлений современной транспортной науки и техники, отвечающим требованиям экологичности и энергоэффективности. Ключевым аспектом повышения энергетической устойчивости таких систем является рекуперация кинетической энергии при торможении. Однако эффективность этого процесса остается недостаточно изученной и количественно неопределенной, что создает значительные препятствия для оптимизации проектных решений и эксплуатационных режимов.

Систематический обзор существующей литературы показал наличие двух основных подходов к математическому моделированию энергоэффективности в системах магнитолевитационных поездов: онлайн-алгоритм оптимизации качения, использующий псевдоспектральный метод для оптимизации траектории с учетом рекуперации энергии [1], и стратегия управления переменной частотой скольжения для эффективности тяги линейного асинхронного двигателя [2]. Имеющихся данных недостаточно, чтобы определить, какая модель наиболее точно предсказывает эффективность рекуперации энергии, поскольку ни в одном из исследований не были представлены количественные показатели точности прогнозирования, такие как частота ошибок или коэффициенты корреляции. Более того, два подхода рассматривают разные аспекты энергоэффективности магнитолевитационных поездов — использование рекуперативной энергии несколькими поездами на системном уровне и оптимизацию тяги на уровне двигателей, что делает прямое сравнение точности нецелесообразным.

Подход управления переменной частотой скольжения продемонстрировал более убедительные доказательства применимости в ходе реальных испытаний магнитолевитационного поезда, показав повышение эффективности как тяги, так и общего энергопотребления, в то время как алгоритм оптимизации качения был проверен только с помощью численного моделирования. В обоих исследованиях отсутствовали четкие определения эффективности рекуперации энергии и подробные математические формулировки. Факты свидетельствуют о том, что для всестороннего прогнозирования эффективности рекуперации энергии потребуется интеграция оптимизации на уровне траектории с учетом рекуперативного торможения от соседних поездов со стратегиями управления на уровне двигателя, хотя количественные сравнения точности в современной литературе пока недоступны.

Таким образом, актуальность настоящего исследования обусловлена необходимостью разработки целостной математической модели, позволяющей дать количественную оценку КПД рекуперации энергии для маглева в рамках полного цикла «разгон-торможение». Целью данной работы является моделирование этого процесса с последующим расчетом доли энергии, возвращаемой в систему. Решение этой задачи позволит заложить основу для последующей интеграции оптимизации траектории на сетевом уровне и стратегий управления на уровне двигателя, что является следующим шагом в создании энергетически оптимальных систем магнитолевитационного транспорта.

2. Материалы и методы.

2.1. Постановка задачи.

Рассчитаем процент энергии, возвращаемой в сеть за один цикл "разгон-торможение" на заданном перегоне. Движение поезда будем рассматривать как движение материальной точки с постоянной массой m. Профиль пути будем считать горизонтальным (игнорируем уклоны). Температура и другие внешние условия постоянны. КПД силовой электроники (инверторов, преобразователей) примем также постоянными.

Модель состоит из двух взаимосвязанных частей: механической и электрической. 

Движения поезда описывается вторым законом Ньютона с учетом силы тяги  (при разгоне), силы торможения  (при рекуперации эта сила положительна и создается линейным двигателем), и силы сопротивления движению :

                                                                             (1)

Сила сопротивления для поезда на магнитной подушке включает в себя аэродинамическое сопротивление  (ρ — плотность воздуха, C_d — коэффициент аэродинамического сопротивления, A — лобовая площадь) и сопротивление, обусловленное магнитным подвесом (вызывается вихревыми токами в полотне и другими эффектами, часто пропорциональна скорости) F_mag = k_mag v, где k_mag —коэффициент, определяемый конструкцией подвеса.

При разгоне линейный двигатель (синхронный или асинхронный) потребляет энергию из сети, преобразуя ее в механическую работу. Потребляемая мощность P_in = F_tractionv/η_inv, где η_inv — КПД инвертора (преобразует постоянный ток в переменный). При торможении линейный двигатель переходит в генераторный режим. Он создает тормозную силу и преобразует кинетическую энергию поезда обратно в электрическую. Генерируемая электрическая мощность P_gen = F_braking v η_gen. Здесь η_gen — КПД системы генерации Эта мощность возвращается в сеть или в накопители.

Энергетический баланс за цикл складывается из энергии, затраченной на разгон E_acc = ∫P_in(t) dt (интегрирование ведется по времени разгона), энергии, рекуперированной при торможении, E_rec = ∫P_gen(t) dt (интегрирование по времени торможения) и энергии, затраченной на преодоление сопротивления E_loss = ∫F_resistancev dt. Эта энергия безвозвратно теряется (в основном, в тепло). КПД рекуперации для цикла можно оценить как: η_cycle = E_rec/(E_acc + E_loss).

2.2. Результаты моделирования.

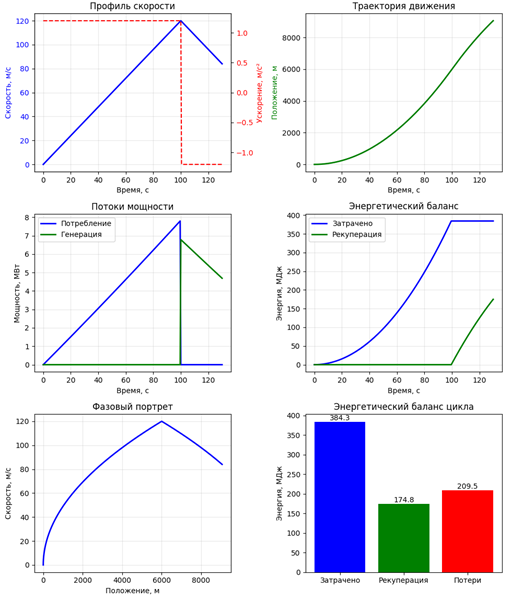
Рисунок 1. Результаты моделирования процесса рекуперации энергии магнитолевитационного поезда за один цикл

Результаты моделирования приведены на рисунке (рис. 1). Для моделирования были выбраны следующие параметры: масса 50 т, максимальная скорость 432 км/ч, длина пути 5 км. Анализ полученных данных показывает, что максимальное значение кинетической энергии достигало 360 МДж, затраченная энергия на разгон составила 384.3 МДж, рекуперация энергии во время торможения составила 174.8 МДж. Эти значения позволяют оценить КПД рекуперации η_cycle ~ 45.5%.

Таким образом, разработанная модель позволяет производить оценки КПД рекуперации энергии магнитолевитационного поезда с учетом различных процессов.

2.3. Обсуждение результатов.

Для полноты рассмотрения нужно учесть влияние типа электромагнитной системы. Для системы на обычных электромагнитах источник магнитного поля – это катушки с железным сердечником, питаемые бортовым источником. Для них характерны Джоулевы потери в обмотках поезда и потери в сердечнике из-за вихревых токов и гистерезиса. Как следствие, часть рекуперированной энергии сразу тратится на питание самих электромагнитов, что снижает общий КПД системы. В случае системы на сверхпроводящих магнитах источник поля – это катушки из сверхпроводящего материала (например, Nb-Ti), охлажденные до температур жидкого гелия (~ 4.2 K) или азота (для ВТСП). Для такого типа системы характерно нулевое омическое сопротивление. В установившемся режиме ток в катушках циркулирует без потерь, а значит не требуется бортовое питание для поддержания поля (только для криосистемы). Возможность создания очень сильных полей увеличивает наводимую ЭДС и тормозную силу. Однако эти особенности сопряжены и с новыми видами потерь. Дополнительная энергия должна потребляться криогенной установкой для поддержания низкой температуры. Это основной источник потерь. Также при движении в проводящих элементах пути (например, в алюминиевом полотне) мощное поле наводит сильные вихревые токи, которые сами по себе создают тормозящую силу и греют полотно. В вакуумном трубопроводе это основной источник потерь на движение с постоянной скоростью и конкурирующий механизм торможения.

3. Заключение.

В данной работе была разработана и применена математическая модель для оценки эффективности рекуперации энергии при торможении поезда на магнитной подушке. Моделирование цикла «разгон-торможение» для поезда массой 50 т на горизонтальном участке длиной 5 км позволило оценить коэффициент полезного действия рекуперации на уровне ~45,5%. Этот результат демонстрирует значительный потенциал систем рекуперативного торможения для повышения энергоэффективности маглева.

Основным ограничением исследования являются принятые упрощения: неизменные внешние условия, постоянные КПД преобразователей и отсутствие учёта профиля пути. Кроме того, полученная оценка эффективности в значительной степени зависит от выбранных параметров модели, таких как коэффициент магнитного сопротивления и аэродинамические характеристики.

Как показал анализ, ключевым фактором, влияющим на общий энергобаланс, является тип электромагнитной системы левитации. Системы на сверхпроводящих магнитах, хотя и требуют затрат на криогенное охлаждение, позволяют минимизировать потери в обмотках и создавать более сильные тормозные усилия, что открывает пути для дальнейшего повышения эффективности рекуперации.

Для более точных прогнозов в будущих исследованиях необходимо интегрировать оптимизацию движения на системном уровне (учёт графика движения нескольких поездов) со стратегиями управления на уровне привода, а также учитывать реальный профиль пути и переменные условия окружающей среды. Предложенная модель служит основой для таких комплексных исследований и может быть использована для сравнительного анализа различных технических решений в области энергосбережения высокоскоростного магнитолевитационного транспорта.