Исследование алгоритма многопараметрической идентификации объединенного принципа максимума

Study of algorithm of multiparameter identification of the combined maximum principle

Igor Pugachev

postgraduate Don state Technical University, Russia, Rostov– on– Don

Irina Pavlova

Candidate of Engineering Sciences, docent Don Cossack state Institute of food technology and business Federal state budgetary educational institution of higher professional education "Moscow state University of technologies and management named K. G. Razumovskiy, Russia, Rostov– on– Don

Arina Eroshenko

Candidate of Engineering Sciences, Don Cossack state Institute of food technology and business Federal state budgetary educational institution of higher professional education "Moscow state University of technologies and management named K. G. Razumovskiy, Russia, Rostov– on– Don

«Работа выполнена по грантам РФФИ № 18-38-00937 мол_а, № 18-08-01494 А» 

Анотация. В докладе предложен новый метод идентификации, полученный на основе аппарата асинхронного варьирования. Использование данного метода

дает эффективный в плане точности оценок, скорости сходимости и снижения вычислительных затрат алгоритм идентификации параметров механических систем, что демонстрируется результатами численного моделирования процесса одновременной идентификации нескольких параметров динамической системы.

Abstract. The report proposes a new method of identification, obtained on the basis of the asynchronous variation apparatus. The use of this method provides an efficient algorithm for identifying the parameters of mechanical systems in terms of accuracy of estimates, convergence rate and reducing computational costs, which is demonstrated by the results of numerical simulation of the simultaneous identification of several parameters of the dynamic system.

Ключевые слова: идентификация; объединенный принцип максимума; динамическая система.

Keywords: identification; combined maximum principle; dynamic system.

Введение. Эффективное функционирование современных механических систем в сложных условиях эксплуатации достигается постоянным контролем их параметров, что позволяет обеспечить своевременную выработку корректирующих воздействий для стабилизации исправного состояния. При этом между вероятностью сохранения исправного состояния механического объекта и точностью контроля существует неразрывная связь, что определяет задачу повышения точности определения параметров чувствительных элементов систем диагностики и контроля как актуальную научную задачу. Один из наиболее общих подходов к её решению заключается в использовании методов идентификации [1].

Традиционно при реализации современных систем контроля используются методы идентификации, базирующиеся на принципах статистического синтеза и приводящие к алгоритмам адаптивной динамической фильтрации [2]. Однако необходимость расширения пространства состояний исходной системы, а также достаточно высокая степень эвристики алгоритмов адаптации приводят на практике к низкой точности и устойчивости получаемых решений.

Постановка задачи. Принято, что при движении системы из начального состояния t=t₀, , в конечное состояние t=t₁, , под действием обобщенных сил  выполняется соотношение, аналогичное принципу Гамильтона - Остроградского для интеграла действия [3]

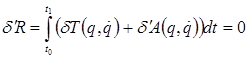,                                                                                    (1)

где    – кинетическая энергия динамической системы,

 – обобщенная координата и скорость,

A – работа обобщенной внешней силы,

 – время начала и окончания процесса,

′ – знак, обозначающий бесконечно малую величину, не являющуюся вариацией. Из требования (1) следует справедливость дифференциального уравнения Лагранжа второго рода [3-5]

, .                                                                           (2)

Пусть форма уравнения (2) известна и имеет следующий вид

,                                                                                (3)

где    - неизвестный параметр,

f - функция, непрерывная вместе со своими частными производными.

Пусть динамика идентифицируемого параметра z описывается уравнением

, ,                                                                    (4)

где    - возмущение, имеющее смысл управления.

Для (4) равенство, аналогичное (1), принимает вид

,                                                                            (5)

из которого вытекает уравнение Лагранжа второго рода в следующей форме

,                                                                             (6)

где   – кинетическая энергия динамики параметров,

A – работа возмущения.

Уравнение наблюдения имеет вид

,                                                                                         (7)

где    - наблюдение,

 - непрерывная вместе с частными производными функция,

n(t) – белый гауссовский шум с известными локальными характеристиками.

Необходимо определить оценки параметра  из условия минимума функционала невязки

,                                                                    (8)

где    – константа, характеризующая интенсивность шумов наблюдения [6].

Согласно [7-11] уравнения последовательной идентификации алгоритма многопараметрической вариационной идентификации динамических систем примут вид

                                           (9)

Пример. Пусть неизвестны параметры динамической системы второго порядка [12-16]

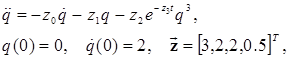                                                                  (10)

а уравнение наблюдения имеет вид

.                                                                                               (11)

Требуется идентифицировать параметры из условия минимума целевого функционала

                                                                                     (12)

Решение поставленной задачи (10) – (12) на основе синтезированного алгоритма многопараметрической вариационной идентификации (9) и использования метода интегральных связок определяется следующей системой уравнений

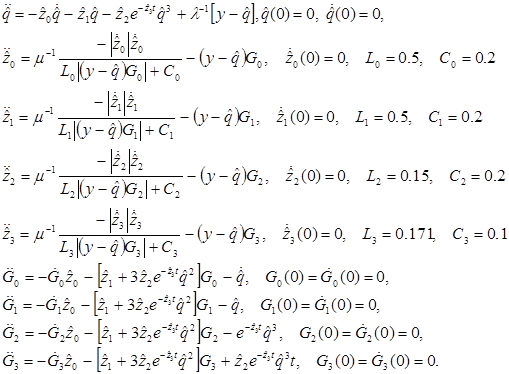                                                       (13)

Результаты численного моделирования представлены на рисунках 1 - 4.

Их анализ позволяет сделать вывод о работоспособности нового алгоритма. Относительная погрешность оценок параметров составляет соответственно , , , .

Список литературы:

1. Залесков А.С., Калиенко И.В., Костоглотов А.А., Лазаренко С.В., Пугачев И.В. Объединенный принцип максимума в задаче структурного синтеза систем с заданным состоянием на основе функций Крылова // Современные тенденции развития науки и технологий. 2015. № 7-3. С. 67-71.

2.  Лурье А. И. Аналитическая механика. –М.: Государственное издательство физико - математической литературы, 1961. – 453 c.

3. Фарина А., Студер Ф. Цифровая обработка радиолокационной информации. Сопровождение целей: Перевод с англ. – М.: Радио и связь, 1993. – 319 c.

4. Kostoglotov A., Kuzin A., Lazarenko S., Pugachev I. The combined maximum principle in the problem of synthesis of an adaptive dynamic filter under conditions of disturbances in the measurement process // В сборнике: MATEC Web of Conferences 13. Сер. "13th International Scientific-Technical Conference "Dynamic of Technical Systems", DTS 2017" 2017. С. 05009.

5. Пугачев И.В., Андрашитов Д.С., Костоглотов А.А., Лазаренко С.В., Вариационный метод идентификации адаптивных динамических систем с построением дополнительных инвариантов // Информационно-измерительные и управляющие системы. 2016. Т. 14. № 11. С. 55-63.

6. Lazarenko S.V., Pugachev I.V., Kostoglotov A.A., Deryabkin I.V. The synthesis of algorithms for parameters estimation of adaptive systems // В сборнике: 2017 International Conference on Mechanical, System and Control Engineering, ICMSC 2017 2017. С. 267-271.

7.  Lazarenko S.V., Pugachev I.V., Kostoglotov A.A., Deryabkin I.V., Andrashitov D.S. The synthesis of the algorithms for state estimation and the parameters of measurement converters based on the combined maximum principle in the problems of dynamic error correction // В сборнике: 2017 International Conference on Mechanical, System and Control Engineering, ICMSC 2017 2017. С. 292-296.

8. Костоглотов А.А., Дерябкин И.В., Пугачев И.В. Синтез модели динамического процесса с нестационарными возмущениями в квазидетерминированном приближении на основе максимума функции обобщенной мощности // Современные тенденции развития и перспективы внедрения инновационных технологий в машиностроении, образовании и экономике. 2016. Т. 2. № 1. С. 79-87.

9. Kostoglotov A., Lazarenko S., Losev V., Pugachev I. The synthesis of adaptive multi-mode regulators based on combined control of the combined maximum principle // В сборнике: MATEC Web of Conferences 13. Сер. "13th International Scientific-Technical Conference "Dynamic of Technical Systems", DTS 2017" 2017. С. 05007.

10. Павлова И.В., Болдырев А.В. Выбор пассивных компонентов в цепях управления IGВТ // Современные проблемы и пути их решения в науке, производстве и образовании. 2014. № 1 (1). С. 7-11.

11. Сейдж Э.П., Мелс Д.Л. Идентификация систем управления. М.: Наука, 1974.– 246 c.

12. Костоглотов А.А., Костоглотов А.И., Лазаренко С.В., Ценных Б.М. Метод структурно-параметрической идентификации лагранжевых динамических систем в задачах обработки измерительной информации // Измерительная техника. 2014. № 2. С. 32-36.

13.  Костоглотов А.А., Лазаренко С.В., Андрашитов Д.С., Кузин А.П. Идентификация параметров мэмс датчиков на базе вариационных принципов в задачах мониторинга железнодорожной инфраструктуры // Информатизация и связь. 2017. № 4. С. 50-55.

14. Костоглотов А.А., Лазаренко С.В., Андрашитов Д.С., Дерябкин И.В. Вариационный метод многопараметрической идентификации динамических систем на основе итерационной регуляризации // Успехи современной радиоэлектроники. 2012. № 6. С. 67-72.

15.  Андрашитов Д.С., Дерябкин И.В., Костоглотов А.А., Лазаренко С.В., Ценных Б.М. Метод коррекции динамической погрешности акселерометра с текущей идентификацией его параметров на основе объединенного принципа максимума // Радиотехника. 2014. № 12. С. 17-23.

16. Костоглотов А.А., Лазаренко С.В., Андрашитов Д.С. Регуляризированный алгоритм многопараметрической вариационной идентификации динамических систем // Сервис в России и за рубежом. 2011. № 8 (27). С. 25-36.