Решение задачи прогнозирования при помощи градиентного бустинга над решающими деревьями

Введение

Темпы развития искусственного интеллекта в настоящее время растут с каждым годом. За последние четыре десятилетия огромные успехи в области компьютерных технологий значительно повлияли на все сферы человеческой деятельности.

Более того, по мнению многих ученых и специалистов из раз­личных областей, искусственный интеллект повлияет на наше будущее сильнее, чем любое другое нововведение в этом веке. Любой компании в наше время для того, чтобы держаться на плаву, требуется эффективно использовать современные технологии по обработке и анализу накопленных данных для решения своих проблем и задач.

Весьма сложный характер многих проблем реального мира, однако, часто означает, что изобретение специализированных алгоритмов, которые будут решать их идеально каждый раз, непрактично, если не невозможно. К подобным проблемам, решаемым при помощи машинного обучения, можно отнести медицинскую диагностику и прог­нозирование оттока клиентов телекоммуникационной компании [1, c. 9].

Данные проблемы можно рассматривать как задачу классификации данных. Классификация в таком случае представляет собой ввод набора данных о человеке и определение класса или вероятность принадлеж­ности к определенному классу. Одним из наиболее эффективных методов классификации на сегодняшний день является градиентный бустинг над решающими деревьями.

Постановка задачи

Реализовать метод градиентного бустинга над решающими деревь­ями для прогнозирования оттока клиентов и диагностики эпилепсии.

Входные наборы данных:

a)   Данные телекоммуникационной компании об активности клиентов

b)   Результаты электроэнцефалографии пациентов

Выходные данные:

a)   Класс, к которому относится клиент – факт отказа, а также вероятность отказа от услуг компании.

b)   Класс, к которому относится пациент – болен эпилепсией или нет, а также вероятность наличия данного недуга.

Реализация метода градиентного бустинга

Идея метода состоит в том, чтобы последовательно строить компо­зицию решающих деревьев [4], каждое из которых ориентируется на примеры, которые предыдущие модели считали сложными и ошибочно классифицированными, стремится уменьшить значение функции потерь.

Алгоритм построения модели градиентного бустинга [2, c. 3]:

Шаг 1. Отбираем набор признаков 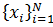 и набор целевых переменных 

Шаг 1. Построить первое решающее дерево в композиции 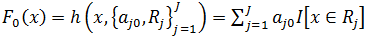 по данным  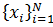и , где  число листовых вершин.

Шаг 2. Перенастраиваем параметры дерева, минимизируя функцию потерь .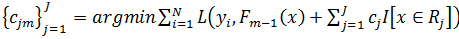

Шаг 3 Прибавляем к имеющемуся алгоритму новое решающее дерево .

Шаг 4. Повторяем шаги 2 и 3 M раз, где M – количество деревьев.

Шаг 5. При помощи композиции 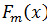 совершаем прогнозы на тестовых данных.

Шаг 6. Оцениваем точность прогнозирования.

Для определения гиперпараметров модели градиентного бустинга был использован скользящий контроль [3], в результате которого для задачи прогнозирования оттока клиентов наиболее эффективными пара­метрами являются – 200 деревьев, коэффициент скорости обучения 0.3, максимальная глубина деревьев 4, а для диагностики эпилепсии – 250 деревьев, коэффициент скорости обучения 0.1, максимальная глубина деревьев – 5.

Обучение и тестирование модели градиентного бустинга

Обучение моделей происходило на следующих наборах данных:

1) Данные телекоммуникационной компании об активности клиентов

2) Результаты электроэнцефалографии пациентов

Первый входной набор данных представляет собой 7043 вектора по 20 элементов в каждом. Так как данные содержат категориальные признаки, то перед построением модели происходит обработка приз­наков, а именно по принципу One-Hot Encoding считается количество уникальных категориальных значений в столбце и формируется взамен данного признака разреженная матрица, где каждый столбец соот­ветствует одному целочисленному возможному значению признака (бинаризация данных). Далее происходит масштабирование всех признаков, чтобы они находились на отрезке [0; 1].

Второй набор данных содержит 11500 объектов, каждый из которых состоит из 29 целочисленных признаков. Поскольку набор не содержит категориальных признаков, необходимо лишь произвести масштаби­рование всех признаков перед использованием в прогнозировании.

С помощью открытых библиотек машинного обучения sklearn и XGBoost была реализована описанная выше модель классификации и обучена на подготовленном наборе данных.

Перед обучением исходные данные были распределены по двум наборам: набор для обучения (80 % объектов) и набор для тестирования (20 % объектов). Оценка точности прогнозирования на тестовых данных производилась с использованием таких метрик качества, как доля правильных ответов и ROC-AUC [1, c. 78].

Полученные оценки точности работы алгоритма приведены в сводной таблице 1:

Таблица 1.

Результаты тестирования

Заключение

Проведённые эксперименты продемонстрировали высокую эффективность применения градиентного бустинга над решающими деревьями при решении задачи бинарной классификации. средние оценки которого для обоих наборов данных составили 82.57 и 98.44 соответственно. Это связано прежде всего с эффективным исполь­зованием решающих деревьев для классификации и практически неограниченным уменьшением частоты ошибок на независимой тестовой выборке по мере наращивания композиции деревьев.