Построение каскадного нейросетевого фильтра для решения задачи кластеризации

Введение

Быстрый рост объемов данных и совершенствование технологий их сбора и хранения повышают потребность в передовых методах анализа и инструментах для извлечения значимой информации из данных. Кластерный анализ - это метод, который может помочь понять большие данные. Его цель - разделить большие наборы данных на значимые подмножества (кластеры) элементов. Затем кластеры могут использоваться для агрегирования, упорядочения, изучения данных, прогнозирования и обнаружения аномалий исследуемых объектов. Кластеризация является действенным инструментом анализа данных [1, c. 1].

Целью работы является проектирование и программная реали­зация моделей кластеризации данных на основе последовательного использования самоорганизующихся карт Кохонена с различной степенью детализации информации (каскадный фильтр) для неодно­родных данных, а также сравнительный анализ возможностей данной модели с не нейросетевыми аналогами.

Постановка задачи

Разработать модель и программную реализацию многомерной нейросетевой кластеризации данных на основе последовательного использования SOM (самоорганизующиеся карты Кохонена).

Провести численные эксперименты по кластеризации данных:

a)    измерения уровня загрязнений воды в водоемах РТ

b)   измерения об активности здоровых пожилых людей при помощи разработанной модели.

Провести сравнительный анализ результатов экспериментов.

Реализация SOM

Модель нейронной сети Кохонена можно описать следующим алгоритмом [3]:

1)   Определение значений параметров алгоритма: используемые метрики: 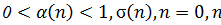 – номер итерации.

2)   Инициализация: выбор значений для начальных весовых векторов 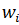 нейронов 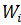. В качестве начальных значений задаются значения, случайно выбранные из обучающей выборки.

3)   Выбор произвольного входного вектора 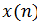 из множества входных данных.

4)   Поиск нейрона-победителя . То есть необходимо найти расстояние от наблюдения 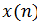 до векторов веса всех нейронов карты и определить из них ближайший по весу узел :

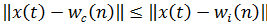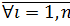,                                                                                        (1)

Если находится несколько нейронов победителей, то случайным образом выбирается один из них.

5)   С помощью функции соседства h определить “меру соседства” нейронов 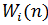 и 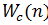 , а так же изменение их векторов веса.

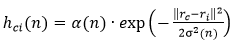                                                                                             (2)

6)   Изменить вектора веса по формуле:

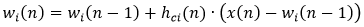                                                                               (3)

Таким образом, вектора веса всех нейронов 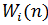, являющихся соседями нейрона-победителя 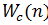, приближаются к рассматриваемому наблюдению.

7)   Вычисление ошибки карты как среднее арифметическое расстояние между наблюдениями и векторами веса соответствующих им нейронов-победителей:

                                                                                                         (4)

где -количество элементов набора входных данных.

Разработка модели каскадной кластеризации данных

Модель многомерной каскадной кластеризации основана на последовательном использовании сети Кохонена для групп данных с возрастающей степенью их детализации. На начальном этапе происходит разбиение всего исходного набора данных на кластеры – формируется первый слой нейросетевого SOM-каскада. Далее, если степень однородности данных в каком-либо кластере нас не устраивает, то кластеризация сетью Кохонена применяется конкретно к данному кластеру. В результате сформировался второй слой SOM-каскада. Процесс завершается, когда будет достигнута приемлемая степень однородности данных во всех кластерах. На рисунке 1 представлена структурная схема четырехуровневой кластеризации [2, c. 74]:

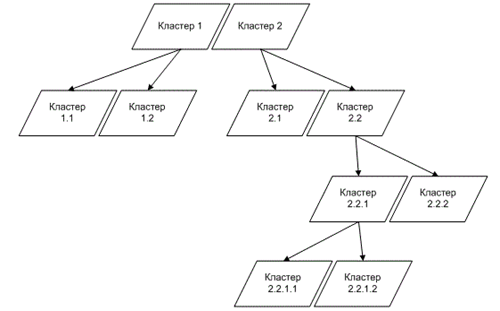
Рисунок 1. Структурная схема четырехуровневой кластеризации

Тестирование каскадной модели и сравнительный анализ

Применительно к поставленной задаче, все модели данных должны будут выполнить разбиение каждого из исходных наборов данных на 4 кластера:

1) Данные измерений уровня загрязнений воды в водоемах РТ. Входной набор данных представляет собой 210 вектора по 27 элементов в каждом. Данные разбиваются на 4 кластера на основе информации об уровне минерализации: низкий, средний, выше среднего и высокий уровень минерализации водоема.

2) Данные об активности здоровых пожилых людей, использующие датчик двигательной активности. Набор данных содержит 304 вектора, каждый из которых состоит из 7 элементов. Данные кластеризуются на 4 группы с ожидаемыми признаками вида активности: сон, отдых на кровати, отдых на стуле, прогулка.

Метод каскадной нейросетевой фильтрации сравнивался с результатами классических методов кластеризации: k-средних и агломеративным иерархическим методом. Критериями эффективности каждой модели выступали:

· точность – процент правильно классифицированных данных;

· коэффициент силуэта - чем выше значение, тем лучшая струк­тура кластеров;

· коэффициент FM - чем ниже коэффициент, тем более отличны кластеры друг от друга.

В Таблице 1 приведены результаты сравнения классических алгоритмов кластеризации с каскадным нейросетевым фильтром.

Таблица 1.

Результаты тестирования моделей

Таблица 2 отражает свойства нейросетевого фильтра в зависимости от количества каскадов.

Таблица 2.

Результаты тестирования модели каскадной кластеризации сетью Кохонена

Выводы

По полученным результатам можно сделать следующие выводы:

1) Каскадный нейросетевой фильтр на основе SOM продемонстри­ровал высокую эффективность работы для обоих наборов данных по сравнению с классическими алгоритмами (метод k-средних и агломера­тивная иерархическая кластеризация). Все три использованные в работе критерия оценки эффективности кластеризации подтверждают данный вывод.

2) Степень точности каскадного фильтра зависит от количества слоев SOM-каскада нелинейно: с ростом количества слоев точность вначале увеличивается, но затем происходит спад. Это обусловлено уменьшением кортежей данных в каждом кластере по мере роста каскада, что в конце концов приводит к их недостатку на очередном этапе.

Заключение

Проведённые эксперименты продемонстрировали высокую эффек­тивность применения каскадного нейросетевого фильтра, основанного на самоорганизующихся картах Кохонена.

Алгоритм каскадной нейросетевой фильтрации может с успехом применяться для кластеризации данных с заданной степенью детализации.