Диофантово уравнение четвёртой степени от трёх переменных
Конференция: XXVI Международная научно-практическая конференция «Научный форум: технические и физико-математические науки»
Секция: Математическая логика, алгебра и теория чисел

XXVI Международная научно-практическая конференция «Научный форум: технические и физико-математические науки»
Диофантово уравнение четвёртой степени от трёх переменных
DIOPHANTINE EQUATION OF THE FOURTH DEGREE IN THREE VARIABLES
Lydia Bokareva
Applicant for the Federal State Budgetary Educational Institution of Higher Professional Education "Novosibirsk National Research State University"
Nikita Bokarev
2-year student of the Faculty of Economics Federal State Budgetary Educational Institution of Higher Professional Education "Novosibirsk National Research State University"
Аннотация. В работе рассмотрен частный случай уравнения Ферма и некоторые уравнения четвёртой степени от трёх переменных, найдена общая формула нахождения всех решений неопределённого уравнения четвёртой степени с тремя переменными х4 + у² = z², где х, у, z ϵ N, то есть формулу, которая позволяет найти все прямоугольные треугольники, один из катетов которых является точным квадратом натурального числа. Использование арифметических функций позволило записать найденные решения в виде единой формулы.
Abstract. In this paper, a special case of the Fermat equation and some fourth-degree equations in three variables is considered. A general formula for finding all solutions of an indefinite fourth-degree equation with three variables x4 + y² = z², where x, y, z ϵ N, that is, a formula that allows finding all right-angled triangles, one of the legs of which is an exact square of a natural number, has been found. The use of arithmetic functions allowed us to write the solutions found in the form of a single formula.
Ключевые слова: диофантово уравнение, уравнения четвёртой степени от трёх переменных.
Keywords: Diophantine equation, the fourth degree equation in three variables.
Рассмотрим уравнение
х4 + у² = z² (1)
где x, y, z ϵ N.
Перепишем уравнение (1) следующим образом:
х4 = (z + у) (z – у) (2)
и пусть
х = рх1, у = ру1, z = рz1, (3)
где (х1, у1, z1) =1. Тогда уравнение (3) примет вид
р² х1 = (z1 + у1) (z1 + у1) (4)
Пусть так же
z1 + у1 = а, z1 - у1 = b, (5)
откуда
 , (6)
, (6)
где (а, b) = 1, тогда равенство (4) запишется:
р2 х14 = ав. (7)
Покажем, что (а, b) ≤ 2. Так как (х1, у1, z1,) = 1, то (у1, z1) = 1, что весьма несложно проверить. Пусть (а, b) = d, тогда
а = d а1 , b = d b1,
где а1, b1 ϵ N, (а1, b1) = 1 и, поэтому, а1 и b1 не могут быть одновременно чётными. Таким образом, из выражений (6) следует, что
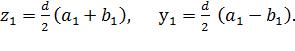
Имеем
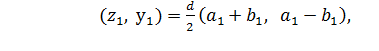
откуда
 (8)
(8)
Как видно из выражения (8), или d = 1 (а1 и b1 – оба нечётные), или d = 2 (а1 и b1 – разной чётности). Итак,
(а1, b1) ≤ 2. (9)
Рассмотрим уравнение (7) при условии (9). Очевидно, что р² | (аb), следовательно, можно записать
![]() (10)
(10)
где рi , a´, b´ ϵ N ![]() ), (a´, b´ ) ≤ 2. Подставив выражение (31) в равенство (7) получим:
), (a´, b´ ) ≤ 2. Подставив выражение (31) в равенство (7) получим:
х14 = а´· b´, (11)
где a´, b´ ϵ N, (a´, b´ ) ≤ 2. Рассмотрим отдельно два случая (a´, b´ ) = 1 и (a´, b´ ) = 2.
1) Пусть (a´, b´ ) = 1. Тогда из уравнения (11) следует, что
a´ = m4, b´= n4, (12)
где m, n ϵ N, (m, n) = 1. В этом случае, вспомнив условия (2) и (5), получим следующую формулу:

![]()
где р, m, n ϵ N, (m, n) = 1, ![]() р – свободное от квадратов число. Поскольку у, z ϵ N имеем формулу:
р – свободное от квадратов число. Поскольку у, z ϵ N имеем формулу:


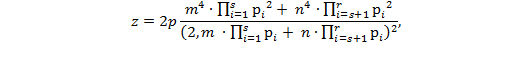
где р, m, n ϵ N, (m, n) = 1, ![]() р – свободное от квадратов число.
р – свободное от квадратов число.
В справедливости формулы (13) легко убедиться, подставив её в уравнение (1). Полагая фиксированными натуральными числами, отвечающими условиям, наложенным на них, получим частные решения уравнения (1). Например, р = 2, m = n = 1: ‹2, 3, 5›; р = 1, m = 2, n = 1: ‹4, 30, 34› и так далее.
2) Пусть теперь (a´, b´ ) = 2. Тогда
а´ = 2aʺ, b´ = 2bʺ, (14)
где (aʺ, bʺ ) = 1 и, следовательно, уравнение (7) примет вид
х14 = 4·аʺ· bʺ,
где aʺ, bʺ ϵ N, (aʺ, bʺ ) = 1. Очевидно, что х должно делиться на 2, то есть, х1 = 2х2 , а, значит, 4х24 = аʺ· bʺ,. Таким образом, или 4 | аʺ, или 4 | bʺ. В первом случае, aʺ = 4m4, bʺ = n4, то есть, х2 = mn, х1 = 2mn. Вспомнив выражения (14), (11), (6), (1), получим формулу
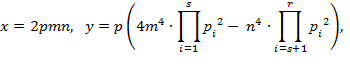
![]() (15)
(15)
где р, m, n ϵ N, (m, n) = 1, n – нечётно (так как (aʺ, bʺ ) = (4m4, n) 4= 1), 2m² ![]() > n²
> n² ![]() . Если же 4 | bʺ, то по аналогии получим:
. Если же 4 | bʺ, то по аналогии получим:
![]()
![]() (16)
(16)
где р, m, n ϵ N, (m, n) = 1, m – нечётно (так как (aʺ, bʺ ) = (m4, 4n) 4= 1), m² ![]() > 2n²
> 2n² ![]() .
.
Формулы (36) и (37) можно объединить в единую формулу

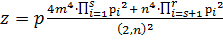 , (17)
, (17)
где р, m, n ϵ N, (m, n) = 1, р = ![]() (рi = рj тогда и только тогда, когда i = j), 2m²
(рi = рj тогда и только тогда, когда i = j), 2m² ![]() > n²
> n² ![]() .
.
Полагая в формуле (17) р, m, n конкретными натуральными числами, отвечающими условиям, наложенным на них, получим частные решения уравнения (1). Например, р = m = n = 1: ‹2, 3, 5› и так далее.
Видно, что при некоторых параметрах формулы (13) и (17) могут давать одинаковые частные решения уравнения. Можно показать, что формула (17) является частным случаем формулы (13).
Действительно, положим в формуле (13) р = 2р´, тогда в этой формуле (2, 2m![]() + n
+ n![]() и, следовательно, формула (34) примет вид
и, следовательно, формула (34) примет вид

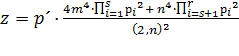 , (18)
, (18)
где р´, m, n ϵ N, (m, n) = 1, р´ = ![]() (рi = рj тогда и только тогда, когда i = j), 2m²
(рi = рj тогда и только тогда, когда i = j), 2m² ![]() > n²
> n² ![]() . Если в формуле (17) положить, что р – нечётное число, тождественность формул (17) и (18) очевидна.
. Если в формуле (17) положить, что р – нечётное число, тождественность формул (17) и (18) очевидна.

 ,
,
или
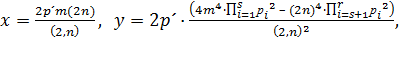
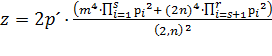 ,
,
где р, m, n ϵ N, (m, n) = 1, р=![]() (рi = рj тогда и только тогда, когда i = j). Несложно показать, что обе формулы являются частным случаем формулы (13), достаточно положить в формуле (13) р – нечётным числом и, в первом случае, m = 2m1, во втором – n = 2n. Таким образом, формула (17) является частным случаем формулы (13).
(рi = рj тогда и только тогда, когда i = j). Несложно показать, что обе формулы являются частным случаем формулы (13), достаточно положить в формуле (13) р – нечётным числом и, в первом случае, m = 2m1, во втором – n = 2n. Таким образом, формула (17) является частным случаем формулы (13).
Итак, все решения уравнения (1) можно записать в виде единой формулы:
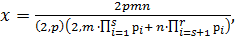
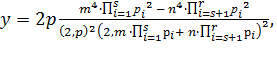 (19)
(19)
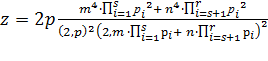 ,
,
где р, m, n ϵ N, (m, n) = 1, m² ![]() > n²
> n² ![]() , р – свободное от квадратов число.
, р – свободное от квадратов число.
При фиксированных натуральных числах m и n можно найти частные решения. Например, варьируя параметры в формуле (19) получим частные решения уравнения (1), некоторые из которых приведены в таблице ниже:
|
р |
m |
n |
х |
у |
z |
х4 + у² = z² |
|
1 |
1 |
1 |
2 |
3 |
5 |
24 + 3² = 5² |
|
1 |
3 |
1 |
3 |
40 |
41 |
34 + 40² = 41² |
|
1 |
3 |
2 |
12 |
17 |
145 |
124 + 17² = 145² |
|
2 |
1 |
1 |
4 |
30 |
34 |
44 + 30² = 34² |
|
2 |
3 |
2 |
6 |
77 |
85 |
64 + 77² = 85² |
|
3 |
1 |
1 |
3 |
12 |
15 |
34 + 12² = 15² |
|
3 |
3 |
2 |
36 |
540 |
1404 |
364 + 540² = 1404² |
|
3 |
3 |
2 |
36 |
8700 |
8700 |
364 + 8700² = 8796² |
|
5 |
1 |
1 |
10 |
495 |
505 |
104 + 495² = 505² |
|
5 |
1 |
2 |
20 |
420 |
580 |
204 + 420² = 580² |
|
6 |
1 |
1 |
12 |
192 |
240 |
124 + 192² = 240² |
|
6 |
1 |
1 |
12 |
420 |
444 |
12² + 420² = 444² |
|
|
|
|
|
|
|
|


