Динамика релятивистского пучка электронов и возбуждаемого им поля на начальной стадии процесса в задачах вакуумной СВЧ электроники

Dynamics of a relativistic electron beam and a field excited by it at initial stage of the process in problems of vacuum microwave electronics

Anatoly Kuznetsov

Cand. Phys.-Math. sciences, associate professor, Tula state university, Russia, Tula

Аннотация. Рассматривается принципиальная возможность и необходимость постановки задачи о динамике релятивистского пучка электронов и возбуждаемого им поля в присутствии однородного внешнего магнитного поля конечной величины. Формулируются основные задачи, метод и последовательность разработки линейной теории динамики релятивистского пучка и поля на начальной стадии процесса в задачах вакуумной СВЧ электроники. В общем виде, получена замкнутая система линейных интегро-дифференциальных уравнений, составляющих основу линейной теории электродинамики релятивистского пучка электронов с учётом его самовоздействия в присутствии конечного однородного внешнего магнитного поля стабилизирующего пучок.

Abstract.The fundamental possibility and necessity of formulating the problem of the dynamics of a relativistic electron beam and a field excited by it in the presence of a uniform external magnetic field of finite magnitude is considered. The main tasks, the method and the sequence of development of the linear theory of the dynamics of the relativistic beam and field at the initial stage of the process in problems of vacuum microwave electronics are formulated. In general, a closed system of linear integro-differential equations is obtained that form the basis of the linear theory of electrodynamics of a relativistic electron beam, taking into account its self-action in the presence of a finite uniform external magnetic field of the stabilizing beam.

Создание, совершенствование и оптимизация работы генераторов и усилителей электромагнитного излучения большой мощности, основанных на преобразовании кинетической энергии сильноточных релятивистских электронных пучков в энергию излучения [1,2,3,4], невозможно без строгой теории взаимодействия пучка с порождаемым им электромагнитным полем. Это означает, что электродинамика систем, в которых необходимым элементом является сильноточный релятивистский электронный пучок, должна строиться с учётом самовоздействия, поскольку генерируемое им поле сравнимо с полем, порождаемым внешними источниками, и может даже существенно превышать его [5].

В настоящее время успешно используются программы для численного моделирования электромагнитных процессов в системах различной геометрии, основанные на непосредственном интегрировании уравнений Максвелла и уравнений движения заряженных частиц [6,7,8]. Однако обилие параметров, от которых зависит динамика пучка и возбуждаемого им поля, требует сочетания численного эксперимента с аналитической теорией, позволяющей выяснить роль каждого из них и определить оптимальные условия, обеспечивающие как транспортировку пучка, так и генерацию излучения.

Примером плодотворного сочетания численного эксперимента [9] и аналитической теории [10] является факт полного подавления неустойчивости ленточного пучка в плоском резонаторе. Линейная теория, развитая в работе [10], установила, что для этого достаточно изменения лишь одного геометрического параметра резонатора. На ранней стадии количественно, а на поздней – качественно, эта теория объяснила все особенности динамики пучка и поля, выявленные в численном эксперименте [9]. В [5] так же делается вывод о том, что неустойчивости пучка препятствующие его транспортировки через резонатор, вряд ли могут быть подавлены только подбором геометрических параметров. По-видимому, для стабилизации пучка придется использовать внешнее магнитное поле, что и делается в большинстве технических устройств, обеспечивающих генерацию и усиление электромагнитного излучения. Между тем, в теоретической динамике пучка и поля, имеется, существенный пробел – рассмотрены, два предельных случая: бесконечно сильного внешнего магнитного поля, полностью подавляющего поперечное движение электронов пучка [11], и нулевого магнитного поля [10]. В связи с этим, существует обоснованный интерес к промежуточному случаю – динамике пучка и поля в присутствии однородного внешнего магнитного поля конечной величины, стабилизирующего пучок.

Приступая к анализу динамики пучка и возбуждаемого им поля в присутствии однородного внешнего магнитного поля конечной величины в рамках линейной теории, вначале сформулируем её основные задачи [5]. Эта теория должна установить спектр собственных частот резонатора с пучком, выяснить, какие условия нужны для реализации как нулевых, так и максимальных инкрементов неустойчивости. Помимо того, в её задачу входит определение пространственной структуры волнового поля, в котором движется пучок. Необходимо отметить, что термин неустойчивость в данном изложении употребляется не в классическом смысле неустойчивости какого-либо стационарного состояния, а обозначает факт превращения кинетической энергии электронного пучка в энергию электромагнитного поля, в результате которого энергия поля возрастает во времени.

Решение вопроса об устойчивости пучка должно проводиться в следующей последовательности [5]. Вначале анализируется характеристическое уравнение, связывающее временную и пространственные характеристики возбуждаемого пучком электромагнитного поля. Затем с помощью соответствующих данной частоте волновых чисел поля конструируется его пространственная структура и подставляется в граничные условия, которые в свою очередь определяются геометрией пучка и рассматриваемой электродинамической системы. В результате получаются дисперсионные уравнения, из которых можно определить спектр собственных частот ограниченной системы. Граничные условия приводят так же к соотношениям между комплексными амплитудами волн, имеющих одну и туже частоту, но различные волновые числа. С помощью этих соотношений, после решения дисперсионных уравнений можно окончательно установить пространственную структуру волнового поля, в котором движется пучок.

Для построения линейной теория, используются уравнения Максвелла и бесстолкновительное кинетическое уравнение с самосогласованным полем для функции распределения электронов релятивистского пучка (уравнение Власова) [12,13,14], учитывающее лишь коллективный эффект взаимодействия электронов пучка:

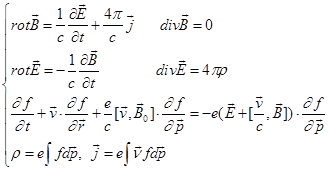
Такой способ описания считается на сегодняшний день наиболее строгим. Предполагается, что имеется однородное внешнее магнитное поле  конечной величины. Электронный пучок инжектируется в резонатор произвольной геометрии с идеально проводящей поверхностью

Линейная электродинамика имеет право не учитывать факт отражения электронов тормозящим их полем. Поэтому на входе пучка в резонатор, в плоскости инжекции электронов, можно считать заданной их функцию распределения по импульсам, аргументы которой учитывают продольное и поперечное движение пучка: . Ее пространственно-временная эволюция автоматически учитывает все дрейфовые движения электронов помимо тех, которые обусловлены неоднородностью внешнего магнитного поля. Одним из часто используемых допущений является предположение о том, что электроны пучка на входе в систему являются моноэнергетическими, что соответствует условию 

Сущность используемого в работе метода [5] заключается в следующем: вначале производится переход от переменных t, z, , , от которых зависит функция распределения электронов по импульсам, к новым переменным, совпадающим с интегралами движения электрона в однородном внешнем магнитном поле. В результате этого перехода левая часть уравнения Власова

преобразуется к виду , что позволяет произвести интегрирование по переменной  вначале в пределах , а затем в пределах . После возвращения к исходным переменным получаются две формулы, имеющие рекуррентный характер. Они позволяют осуществить стандартную процедуру разложения искомой функции распределения релятивистских электронов по степеням амплитуды электрического и магнитного полей, индуцированных пучком в электродинамической системе.

В конечном итоге, в наиболее общем виде, удаётся получить выражения для функции распределения электронов пучка, которые определяют её первые моменты, входящие в уравнения Максвелла, и для самих моментов:

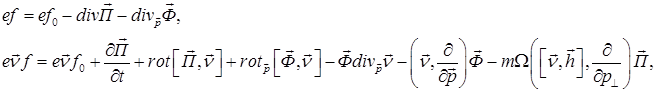
где  - функция распределения электронов по импульсам на входе пучка в резонатор, аргументы которой учитывают продольное и поперечное движение пучка; ;  - единичный вектор, задающий направление внешнего магнитного поля .

Плотности заряда и тока пучка выражаются формулами:

,  

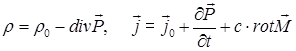где ,    .

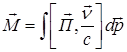Уравнения Максвелла, содержащие плотности заряда и тока пучка, приобретают вид: , .

Вместе с оставшимися уравнениями Максвелла и соответствующими начальными и граничными условиями возникает замкнутая система линейных интегро-дифференциальных уравнений, которая позволяет исследовать на начальной стадии динамику релятивистского пучка и возбуждаемого им поля.

Полученные результаты могут иметь как общетеоретическую значимость для электродинамики сильноточных релятивистских электронных пучков с учетом их самовоздействия, так и практическую, поскольку существует возможность формулировки большого числа конкретных начально-граничных задач, связанных с различной геометрией технических устройств, назначение которых – генерация и усиление электромагнитного излучения высокой мощности. Они позволят теоретически исследовать динамику преобразования в электромагнитную энергию не только кинетической энергии продольного движения электронов пучка, но и энергии их поперечного движения относительно направления стабилизирующего магнитного поля.

Несмотря на то, что исследования имеют непосредственное отношение к вакуумной СВЧ электронике, они в полной мере применимы и в плазменной электронике [14,15,16], которая, естественно, имеет дополнительные проблемы, обусловленные более широким спектром генерируемых частот и нейтрализацией пространственного заряда и тока пучка ионами плазмы. В силу линейности теории ее результаты должны быть автоматически применимы при описании пучково-плазменного взаимодействия.