Об оценках демпфированные осцилляторных интегралов

ON ESTIMATES FOR THE DAMPED OSCILLATORY INTEGRALS

Shahriddin Muranov

doctoral student Samarkand State University, Uzbekistan, Samarkand

Аннотация. В данной работе рассматриваются оценки преобразования Фурье мер, сосредоточенных на аналитических гиперповерхностях, содержащих множитель гашения. В статье рассматривается задача С.Д.Согги и И.М.Стейна об оптимальном убывании преобразования Фурье мер с множителем гашения для произвольных аналитических поверхностей трехмерного Евклидова пространства.

Abstract. In this paper we consider estimates of the Fourier transform measures, concentrated on analytic hypersurfaces containing the of damping factor. The paper presents the solution of the problem S.D.Soggi and I.M. Stein about the optimal decay of the transformation Fourier measures with a damping factor for any analytic surfaces in three-dimensional Euclidean space.

Ключевые слова: осцилляторные интегралы; преобразование Фурье; множитель гашения; максимальный оператор.

Keywords: oscillatory integrals; Fourier transform; damping factor; maximal operator.

Введение

В связи с проблемой об ограничении максимальных операторов,

ассоциированных с гиперповерхностью   С.Д. Согги и И.М.Стейном [1] введены следующие демпфированные осцилляторные интегралы:

                                                                                        (1)

где гауссова кривизна гиперповерхности в точке  - неотрицательная гладкая функция с компактным носителем,  скалярное произведение векторов  и  поверхностная мера. Они доказали, что если  то интеграл (1) убывает в порядке , т.е. убывает оптимально.

Постановка задачи.

Пусть  гладкая гиперповерхность. Найти минимальное значение  такое, что справедлива следующая оценка:

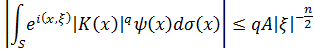
Эта задача была поставлена в работе [1] Согги и Стейна. Частичное решение аналогичной задачи приведено в работе [6] для выпуклых гиперповерхностей конечного линейного типа. Точнее, доказано, что при , преобразование Фурье соответствующей меры, т.е. интеграл (1), убывает оптимально. Решение этой задачи в одномерном случае, точнее когда   кривая, заданная полиномом, вытекает из результатов  Д. М. Оберлина [2].

В данной работе мы представим решение задачи С. Д. Согги и И. М. Стейна для частного класса аналитических поверхностей трехмерного пространства.

Будем считать, что   задается в виде графика некоторой аналитической функции , определенной в малой окрестности начала координат:

где  Если  тогда интеграл  убывает оптимально для любых  когда  Поэтому в дальнейшем будем считать, что . В (2), мы предположим что  - малая окрестность в начале координат и 

Тогда, для функции , мы получим

где 

Таким образом, интегралы (1) имееют  следующий вид

                                                               (3)

где 

Основным результатом настоящей работы является следующая:

Теорема. Пусть  тогда существует окрестность нуля  и  такая, что при любой функции  для интеграла (3) справедлива следующая оценка:

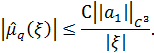
Схема доказательства основной теоремы

Если , то фаза не имеет критических точек и поэтому справедлива.

Лемма 1. Существует окрестность  начала координат, такая,

что для любого  и имеет место следующая оценка:

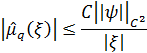
Лемма 3 является аналогом леммы  1 в роботы [3].

Пусть  Тогда, мы записываем интеграла (2) в следующем виде

где   и . Случай  подробно исследован в работе [3]. Более того в этом случае при  интеграл (1) оптимально убывает и поэтому мы предположим, что  бесконечно гладкая функция с достаточно малым носителем и . Поэтому в окрестности нуля обе главные кривизны достаточно малы.

Теперь, множество  разложено на две подмножеств, т.е:

 и 

Сначала, мы изучаем интеграл (3) на множестве .

Предложение 1. Пусть ,  тогда существует окрестность  начала координат и  такое, что для любого  для интеграла (3)

справедлива следующее оценка

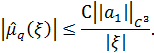
Теперь,  рассмотрим интеграл (3) на множестве .

Предложение 2. Пусть , тогда существуют  малая окрестность  начала координат и  такие, что интеграл (3) удовлетворяет следующее неравенство при всех функция :

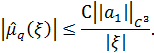
1. C.D. Sogge, E. M. Stein Averages of functions over hypersurfaces in R^n Invent. Math 82543-5561985
2. D.M. Oberlin Oscillatory integrals with polynomial phase MATH.SCAND 69. 45-56. 1991
3. И.А.Икромов, Ш.А.Муранов Об оценках осцилляторных интегралов с множителем гашения Математические заметки 104. 2. 236-251 (2018).
4. Sh.A.Muranov On estimates for oscillatory integrals with damping factor Uzbek Mathematical Journal 4. 112-125.( 2018)
5. Arkhipov G.I., Karatsuba A.A. and Chubarikov V.N., Trigonometric integrals. Izv. Akad. Nauk SSSR Ser. Mat. 43(5), 971-1003 1197 (Russian); English translation in Math. USSR-Izv., 15(1980),pp 21-239.
6. А.С. Садуллаев Критерии алгебраичности аналитических множеств Функц. анализ и его прил 6. 1. 85-86 (1972)
7. И.А. Икромов Демпфированные осцилляторные интегралы и максимальные операторы Математические заметки. 78. 833-852. (2005)
8. А.Эрдейи Асимптотические разложения . М: Физматгиз (1962)
9. М.В. Федорюк Метод перевала Наука. М: (1977)
10. I.A. Ikromov, D. Müller, M. Kempe Damped oscillatory integrals and boundedness of maximal operators associated to mixed homogeneous hypersurfaces Duke Math.J. 126 no.3, 471-490. (2005)