Уравнение Шредингера для волновых функций Блоха

Аннотация. Статья посвящена полупроводникам с низкоразмерными системами, которые активно развиваются и являются относительно новым направлением. Концепция квантовых ям, квантовых нитей и квантовых точек раскрывается в статье. Концепция квантовых состояний важна для технологии активных устройств, например, с помощью этой концепции можно объяснить поведение лазеров на квантовых ямах, фотоприемников, резонансных туннельных диодов и т.д.

Ключевые слова: уравнение Шредингера, полупроводники с низкоразмерными системами.

В реальных полупроводниковых кристаллах энергетический спектр и волновые функции стационарных состояний электронов часто имеют значительно более сложный вид, чем в «стандартной» модели с параболической зоной. Актуальные для практики полупроводниковые материалы (например, такие как полупроводниковые соединения III-V) характеризуются заметной непараболичностью зоны проводимости, сложной картиной ветвей валентной зоны и необходимостью учета спин-орбитального взаимодействия.

В одноэлектронном приближении спектр собственных значений энергии и волновые функции стационарных состояний в полупроводниковой структуре определяются уравнением Шредингера, учитывающим релятивистские поправки и спин электрона:

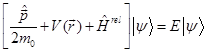                                                                                                   (1)

В этом уравнении  - оператор импульса, m0 - масса электрона в вакууме,  - потенциальная энергия электрона (в отсутствие внешнего магнитного поля) в электростатическом поле всех ионов и электронов, содержащихся в изучаемой системе,  - волновая функция в форме двухкомпонентного спинора, включающая спиновую степень свободы электрона,  - релятивистский вклад в гамильтониан электрона [12]:

                                                                                      (2) 

Здесь  - оператор спина для величины спина  (σ_x, σ_y, σ_z,- матрицы Паули), c - скорость света, × - знак векторного произведения.

Потенциал  в (1) представляет собой в каждом слое гетероструктуры периодическую функцию координат, отражающую атомное строение кристаллической решетки данного слоя. Так, в случае одиночного резкого гетероперехода с плоскостью интерфейса при z = 0, образованного материалами А и В, функция  имеет вид:

                                                                                                       (3)

где  и  - кристаллические потенциалы в слоях А и В.

Для количественного решения уравнения (1) с потенциалом (3) необходимо применять численные методы, аналогичные методам расчета зонной структуры однородных (объемных) кристаллов. Как правило, в таких расчетах потенциал  задается в модельной форме, с подгоночными параметрами, значения которых затем уточняются из сравнения теоретических результатов с экспериментальными данными об энергетическом спектре. Если это обстоятельство учесть заранее, то можно ограничиться более простым выражением для оператора . Так, второе слагаемое из (2) можно включить в потенциал  уравнения (1) и в дальнейшем не выписывать эту релятивистскую поправку явно. Несущественным оказывается также первое слагаемое в (2) - оно приводит к непараболичности энергетического спектра, которая, как мы далее увидим, возникает и без такого слагаемого в гамильтониане. В результате, включение  в гамильтониан уравнения (1) фактически сводится к учету только третьего слагаемого из (2), которое называют спин-орбитальным взаимодействием:

                                                                                                      (4)

В присутствии оператора  собственные состояния  гамильтониана (1) в общем случае уже не имеют вида произведения  не зависящих друг от друга орбитальной  и спиновой функций , а представляют собой линейные комбинации этих произведений, причем, как мы увидим ниже, вырожденные (без учета  уровни энергии E испытывают так называемое спин-орбитальное расщепление. В ряде полупроводниковых материалов спин-орбитальное расщепление зон сравнимо по масштабу с шириной запрещенной зоны, так что член  в уравнении Шредингера оказывается актуальным.

Состояния частиц в гетероструктурах с учетом поля кристаллической решетки естественно искать в форме линейных комбинаций волн Блоха - частных решений уравнения (1) с потенциалом , обладающим полной симметрией однородного кристалла. Вспомним, как определяются эти частные решения.

При наличии трансляционной симметрии кристаллического потенциала  искомые частные решения могут быть выбраны как состояния , собственные для операторов трансляций  на векторы  решетки Браве .

Действие оператора трансляции заключается в замене аргумента волновой функции  на . Такое решение имеет вид

                                                                                                            (5)

где функция  не изменяется при замене  на , то есть она

является периодической функцией координат  с периодами . В этом случае выражение (5) называют волной Блоха или Блоховской волновой функцией, а присутствующий в нем множитель  - Блоховской амплитудой.

С учетом спина электрона Блоховскую амплитуду  следует рассматривать как двухкомпонентный спинор, который может быть представлен линейной комбинацией двух базисных спиноров . Если в качестве базисных спиноров  взять спиновые состояния электрона с определенными значениями проекции спина на ось z,  то Блоховская амплитуда в общем случае запишется в виде

                                                                                                      (6)

где  и  - обычные (однокомпонентные) периодические функции координат.

Действуя оператором импульса на функцию, Блоха (5), получим

Учтем эти равенства, выполняя подстановку выражения (5) в уравнение Шредингера (1) с оператором  в качестве . Разделив левую и правую стороны получившегося равенства на , имеем следующее уравнение для блоховской амплитуды

                                                                                                          (7)

где

                                                                       (8)

Обозначим для краткости:

                                                                                                    (9)

                                                                                             (10, a)

Тогда гамильтониан (8) запишется в виде:

                                                                                   (10, б)

При любом заданном волновом векторе  уравнение (7) представляет собой задачу на собственные значения  и собственные векторы  оператора  (10). Пронумеруем индексом n линейно независимые решения  и соответствующие им собственные значения энергии . Таким образом, приходим к хорошо известному в физике твердого тела результату: энергетический спектр электрона в периодическом поле решетки складывается из множества зон , где n имеет смысл номера зоны.