Алгоритмы многокритериальной оптимизации в задачах выбора параметров системы управления мехатронными модулями.

Мехатронные модули в настоящее время широко используются в различных областях науки и техники. Они представляют собой сложные структурные системы и являются многосвязными. Задача выбора оптимальных параметров системы управления для мехатронных модулей всегда актуальна. Обычно их рассматривают как односвязные структуры и выбирают параметры систем управления исходя из одного критерия. Однако, при таком подходе, упускаются из внимания другие важные критерии, что может привести к их ухудшению и, следовательно, к ухудшению качества всей системы.

К примеру, мы оптимизируем по какому-то критерию время регулирования для двух различных систем. Предположим, что в обоих случаях оно получилось одинаковым. Однако в одном случае переходной процесс получился апериодическим, а в другом – синусоидальным. Можно ли сказать, что параметры второй системы оптимальны, если можно подобрать другое время регулирования, при котором процесс будет апериодическим? И можно ли улучшить качество первой системы? Это наводит на мысль о необходимости применения методов многокритериальной оптимизации для решения данной задачи.

При решении многокритериальных задач оптимизации важнейшую роль играют парето-оптимальные решения (эффективные решения). Решение является оптимальным по Парето, если при замене его любым другим допустимым решением нельзя добиться улучшения значения хотя бы одного из критериев, не ухудшив при этом значения какого-то другого. Только среди таких вариантов и следует выбирать наиболее предпочтительный.

Совокупность таких вариантов решений и называется множеством парето-оптимальных решений. Каждое из парето-оптимальных решений порождает вектор значений критериев, который обладает простым геометрическим свойством: он лежит на границе множества критериальных векторов, которые могут быть получены при использовании всех допустимых вариантов решений.

Совокупность парето-оптимальных решений порождает часть границы множества достижимых критериальных векторов, которую принято называть паретовой границей. Ее анализ имеет огромное прикладное значение, поскольку аппроксимация паретовой границы является основой современных методов многокритериальной оптимизации.

Одной из первых публикаций, посвященных многокритериальному синтезу параметров систем управления, была работа А.М. Летова [1], в которой были выделены критерии, по которым необходимо выбирать параметры систем управления. Можно отметить также попытку постановки задачи многокритериального выбора параметров систем управления [2]. К сожалению, несмотря на большое число публикаций, посвященных задачам синтеза, практически отсутствуют работы, в которых решалась бы задача обоснованного выбора состава группы критериев качества в задачах синтеза регуляторов для систем управления. С одной стороны, необходимо стремиться увеличить число критериев для адекватного учета свойств исследуемой системы; но, с другой стороны, с ростом размерности критериального пространства становятся более сложными алгоритмы выделения компромиссного решения.

Рассмотрим на примере два метода нахождения паретовой границы при решении задач МК-оптимизации настроек параметров регулятора для случая двух критериев (k1 и k2). Один из них называется метод прямоугольников. В качестве критериев качества системы могут быть взяты, например, колебательность и величина, обратная степени устойчивости. Оба данных критерия желательно минимизировать.

Пусть множество строго допустимых точек М_сд задано в виде таблицы (табл. 1). На рисунке 1 показано наглядное изображение данного множества.

Рисунок 1. Множество Мсд

Таблица.1.

Множество М_сд

Нахождение точек паретовой границы состоит из следующих этапов:

1-й этап. Находим точки (точку) с минимальным значением показателя k2. Из табл.1 следует, что минимальное значение k2 имеют две точки: А1(13;2) и А6(16;2). Выбираем из них точку с минимальным k2, в данном случае А1. Очевидно, эта точка является крайней левой точкой левой нижней границы. Снабжаем эту точку знаком +. Отмечаем, что значение показателя k1 в этой точке равно 13.

2-й этап. Исключаем из дальнейшего рассмотрения как худшие (снабжением знака минус или зачёркиванием) все точки, у которых k1>13, а именно точки А6, А8, А9, А10, А11, А12, А13

3-й этап. Находим точки (точку) с минимальным значением показателя k1 (при этом, очевидно, будем рассматривать только те точки, которые до этого не были снабжены знаком), а именно – А2, А15 и А16. Из них выбираем точку с минимальным значением показателя k2 – точку А2. Очевидно, эта точка является крайней правой точкой левой нижней границы и её также отмечаем знаком «+». Отмечаем, что этой точке соответствует k2=9.

4-й этап. Исключаем из дальнейшего рассмотрения все точки, у которых k2>9, а именно точки А14, А15, А15 Далее тем же способом просматриваем все оставшиеся точки (т.е. не отмеченные знаком «+» или «-» или зачеркнутые), применяя к ним последовательно процедуры 1, 2, 3, и 4-го этапов, вплоть до того, пока не останется ни одной точки, не снабжённой знаком «+» или «-» или зачеркнутой. Результат применения метода прямоугольников показан на рисунке 2б.

Помимо вышеуказанного метода существует ещё один способ нахождения точек Парето, именуемый методом рабочих характеристик. В случае двух показателей качества он сводится к нахождению любой из следующих двух рабочих характеристик:

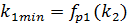                                          (1),

или

                                          (2).

Рассмотрим рабочую характеристику (1). Она получается минимизацией показателя k1 при фиксированном значении показателя k2; при этом минимизация осуществляется для всех допустимых значений показателя k2. Далее, из рабочей характеристики исключаются некоторые точки таким образом, чтобы полученная кривая представляла собой убывающую функцию. Для случая рабочей характеристики (2) решение аналогично, но там минимизируется k2 при фиксированном k1.

Нетрудно убедиться, что для множества Мсд, изображенного на рис.1 рабочая характеристика (1) имеет вид, приведённый на рис. 2,а. она включает в себя все нехудшие точки (A1-A5), а также ряд худших точек (A7, A9, A10, A12, A14, A15, A16).

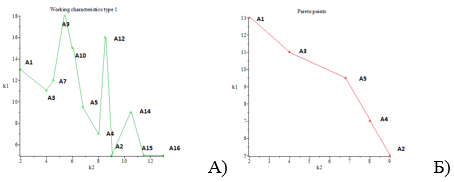
Рисунок 2. а) – рабочая характеристика (1), б) – Паретова граница

Рассмотренные выше алгоритмы имеют большие перспективы применения. Методы многокритериальной оптимизации постоянно модифицируются и совершенствуются. На основе их может быть создан целый ряд программных продуктов, в частности:

·     Программный комплекс для решения задач устойчивости и качества систем управления;

·     Программный комплекс для моделирования оптимальных систем автоматического управления;

·     Интеллектуальная система для выбора и настройки системы управления автономными роботами.

Также следует обратить внимание на варианты усовершенствования самих алгоритмов. В данной работе методы оптимизации рассматриваются лишь для случая двух критериев качества систем управления (т.е. на критериальной плоскости). Однако критериев качества может быть гораздо больше. Следовательно, необходимо разработать методы нахождения точек Парето в пространстве. Решение этой проблемы может быть одним из вариантов путей развития результатов данной работы.