Исследование системы программного управления печью обжига методом Акульшина

Аннотация. В настоящее время уровень автоматизации на существующих печах обжига не удовлетворяет полностью положению развития современной техники автоматизации. Следовательно, необходимо использовать современные способы, средства и технологии.

Целью является улучшение эффективности производства и повышение качества ферритовых изделий путём использования способов, алгоритмов и средств совершенствования технологического процесса.

Методы использования: изучение, моделирование.

В работе представлена разработка системы программного управления методом Акульшина, реализованная в программной среде Visual Studio. 

Ключевые слова: Автоматизация, система программного управления, обжиг в печи, обжиг ферритов.

За последние годы на предприятиях керамической промышленности были созданы условия для ускорения технического прогресса и решения многих важных задач совершенствования техники и технологии. Технический прогресс осуществлялся путем оснащения предприятий современным оборудованием, новыми средствами механизации и автоматизации, внедрения передовой технологии, интенсификации производственных процессов, рациональной организации труда, выпуска продукции, отличающейся наибольшей эффективностью и высоким качеством.

Ферриты – соединения оксида железа Fe₂O₃ с более основными оксидами других металлов, которые являются ферримагнетиками. Обширно используются в качестве магнитных материалов в радиотехнике, радиоэлектронике и вычислительной технике.

Производство ферритов является почти полностью керамическим, только очень малую часть ферритов получают выращиванием монокристаллов. Наиболее сложным в ходе производства ферритовых изделий является процесс их обжига. Именно в процессе обжига образуются главные свойства и физические характеристики ферритов, которые определяют качество выпускаемого товара. Обжиг ферритовых сердечников является важным процессом, так как он воздействует на недостатки феррита (пережог, трещины), а также на механические характеристики (твёрдость, надёжность). Следовательно, необходимо соблюдать тепловой режим, который является главным условием высококачественной тепловой обработки феррита. То есть следует сохранять установленные в печи параметры температуры и давления внутри печи, расхода электроэнергии.

Процесс обжига включает 3 стадии:

- нагревание;

- выдержка при определённой температуре;

- охлаждение изделий.

Параметры режима обжига:

- температура спекания;

- скорость нагрева и охлаждения;

- время выдержки при установленной температуре.

Несмотря на то, что имеется большое число алгоритмов управления процессом обжига в печи, оптимальные алгоритмы исследованы не полностью.

Самым распространённым алгоритмом является ПИД-регулятор. Нахождение параметров настройки для ПИД-регулятора иногда может являться непростой задачей. В этом случае большую значимость имеет информация о разных условиях работы системы, а также её свойствах. Большинство исследуемых систем не допускает наличие перерегулирования процесса переменной от установленной величины. Необходимое требование качества работы системы – постоянство. Процесс ни при каких обстоятельствах не должен меняться, а должен быть стабильным несмотря на внешние воздействия. Помимо этого, имеются конкретные требования к определённым системам, что устойчивость системы должна сформироваться на протяжении определённого промежутка времени. Применение ПИД-регулятора не всегда считается подходящим решением, в особенности учитывая сложность в его настройке. В связи с этим можно применять и другие способы управления технологическими процессами.

Предложенный вариант алгоритма - система программного управления, при котором система обеспечивает изменение регулируемого параметра по заранее заданному закону (во времени). В такой системе (рисунок 1) можно выделить две основные части: программное устройство ПУ, которое формирует сигнал x_п , и систему воспроизведения СВ, которая состоит из управляющего устройства (регулятора) УУ заданного в ПУ изменения выходной координаты y объекта управления y.

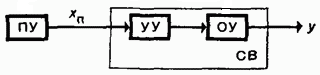
Рисунок 1. Структурная схема программного управления

В системах, содержащих запаздывание для расчета переходных процессов в замкнутых АСР целесообразно применять частотные методы, не требующие вычисления корней характеристического полинома (квазиполинома).

Одним из таких методов является метод Акульшина.

Суть метода Акульшина заключается в следующем. Вместо скачкообразного воздействия амплитуды , рисунок 2, на вход системы подается сигнал в виде прямоугольной волны с периодом Т₀, рисунок 3.

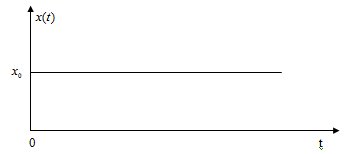
Рисунок 2. Скачкообразное воздействие

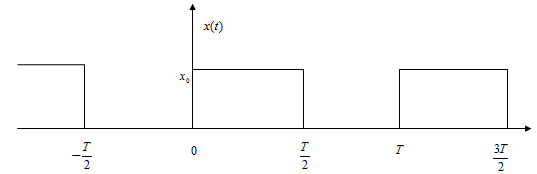
Рисунок 3. Последовательность прямоугольных импульсов

Ниже представлено разложение прямоугольной волны в ряд Фурье. В результате получим ряд, содержащий нечетные гармоники:

,                                                                  (1)

где

 – частота колебаний входных прямоугольных импульсов,

 – постоянная составляющая.

Так как система линейна, то для нее справедлив принцип суперпозиции – реакция на сумму воздействий равна сумме реакций на каждое воздействие в отдельности:

                                                                                                         (2)

Каждая гармоника входного сигнала частоты   и амплитуды 

                                                                                                  (3)

проходя через линейное звено усиливается по амплитуде в  раз и получает фазовый сдвиг . Для входного сигнала, определяемого формулой (1) можно записать:

,

,                                                                             (4)

.

Постоянная составляющая выходного сигнала определяется по формуле

,                                                                                          (5)

где  – коэффициент усиления, значение передаточной функции системы, амплитудно- частотной  и вещественно-частотной  характеристик, соответственно, при нулевом значении аргумента.

Подставляя в формулу (2) выражения (4) и (5) получим выражение для выходного сигнала

 =                                                                        (6)

Формула (6) является основной для расчета переходного процесса.

В некоторых случаях удобнее использовать другую форму записи уравнения (6). Для этого преобразуем следующим образом выражение под знаком суммы

                                                                                (7)

Переходя теперь в (7) к вещественной и мнимой частотным характеристикам

=

,                                                                                                     (8)

получим

                                                                              (9)

Подставляя теперь последнее выражение в формулу (6) получим другое выражение для переходной кривой:

                                                                             (10)

При практических расчетах в формулах (6) и (10) ограничиваются конечным числом гармоник. В результате формулы принимают вид:

                                                                                    (11)

и

,                                                                            (12)

соответственно.

Практика показала, что во многих случаях достаточно пятидесяти гармоник

                                                                                                                (13)

Для построения переходного процесса, как правило, достаточно 24 точек, поэтому при расчетах шаг по времени выбирается по формуле

                                                                                                               (14)

Количество точек, естественно, может быть и увеличено.

Предложенный алгоритм определения состояния системы реализован в интегрированной среде разработки программного обеспечения Visual Studio.

Сконструированная программа обеспечивает:

- ввод текущих значений датчиков;

- мониторинг показаний датчиков;

- предупреждение системы, если температура в печи достигла допустимого уровня;

- отключение системы, если температура в печи достигла предельного уровня.

Для запуска программы необходимо выбрать ярлык программы и дважды щелкнуть на нем левой кнопкой мыши. После запуска программы открывается окно, представленное на рисунке 4. В начале работы задаются необходимые параметры: начальное значение X мощности нагревательных элементов (Вт) в печи. После ввода параметров нажимаем кнопку «Настройка».

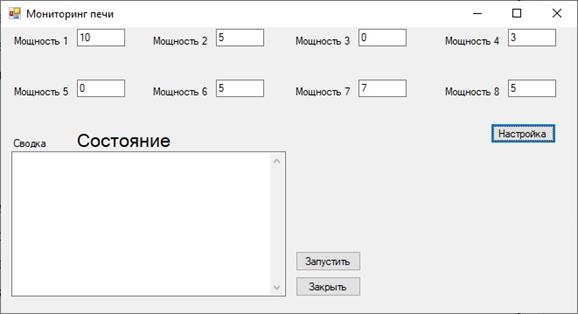
Рисунок 4. Настройка системы

После нажатия кнопки «Настройка» нажимаем на кнопку «Запустить». На рисунке 5 видно, что состояние системы стабильное. Во время работы системы происходит опрос датчиков. Значения датчиков постоянно меняются из-за изменения температуры нагрева в печи.

Рисунок 5. Опрос датчиков

В случае если мощность нагревательных элементов превысит 700 Вт, то система покажет допустимую температуру в печи («Состояние удовлетворительное») и продолжит совершать опрос датчиков, как показано на рисунке 6.

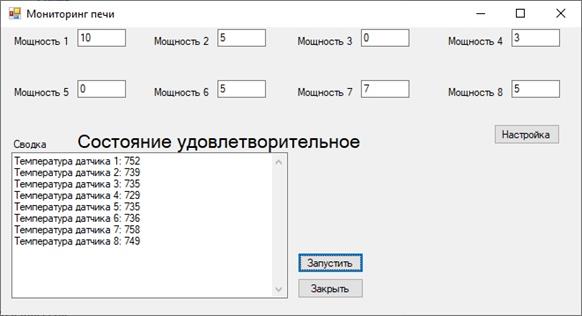
Рисунок 6. Состояние удовлетворительное

Далее, если мощность нагревательных стержней превысила 900 Вт, то состояние системы покажет предельную температуру («Состояние критическое»). Выполняется полная остановка работы печи, следовательно, завершается работа системы (рисунок 7).

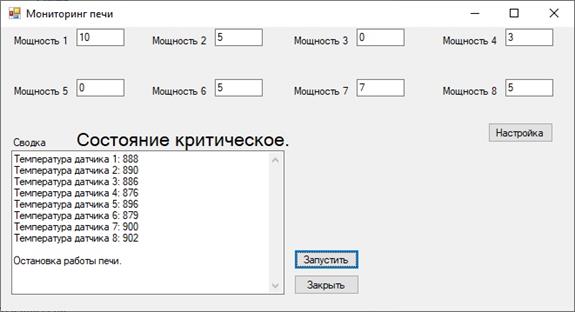
Рисунок 7. Остановка системы