Логарифмы в жизни человека

ВВЕДЕНИЕ

Что такое логарифм? Для чего вообще нужны логарифмы? Какая от них практическая польза? Пожалуй, лучше всего ответил на эти вопросы знаменитый математик, физик и астроном Пьер-Симон Лаплас (1749-1827). По его мнению, изобретение такого показателя, как логарифм, словно удваивает жизнь астрономов, сокращая вычисления нескольких месяцев в труд нескольких дней.

Гениальное изобретение логарифмов, упрощая арифметические операции, облегчает все применения вычисления к реальным предметам и, таким образом, расширяет сферу всех наук, в которых эти численные применения, частные случаи искомой истины являют с одним из способов сравнения с фактами результатов гипотезы или теории и путём этого сравнения позволяют дойти до открытия законов природы. В самом деле, в математике протяженность и усложнение чисто практических вычислений имеют предел, который ни время, ни даже силы не позволяют переходить, и без помощи этих удачных сокращений время отметило бы границы самой науки и предел, который усилия гения не могли бы преодолеть.

ЛОГАРИФМИЧЕСКАЯ СПИРАЛЬ

Самолёт, вылетевший из какой – ни будь точки земного шара на север, через некоторое время окажется над Северным полюсом. Если же он полетит на восток, то, облетев параллель, вернётся в тот же пункт, из которого вылетел. Предположим теперь, что самолёт будет лететь, пересекая все меридианы под одним и тем же углом, отличным от прямого, т. е. держась, всё время одного и того же курса. Когда он облетит земной шар, то попадёт в точку, имеющую ту же долготу, что и точка вылета, но расположенную ближе к Северному полюсу. После следующего облёта он окажется ещё ближе к полюсу и, продолжая лететь указанным образом, будет описывать вокруг полюса сужающуюся спираль.

Так как уравнение этой спирали связано с логарифмической функцией, то вычисленную по этой формуле спираль называют логарифмической.

В математике особо распространены три вида спирали:

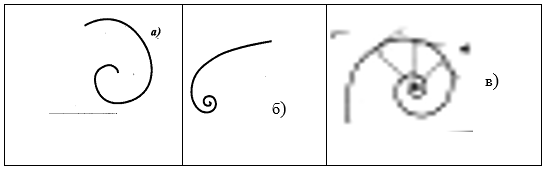
Рисунок 1. Виды спиралей

а) архимедова спираль, б) гиперболическая спираль, в) логарифмическая спираль.

Рассмотрю более подробно логарифмическую спираль. Логарифмическую спираль является траекторией точки, которая движется вдоль равномерно вращающейся прямой, удаляясь от полюса со скоростью, пропорциональной пройденному расстоянию. Если выражаться точнее, то в логарифмической спирали углу поворота пропорционально не само расстояние от полюса до точки кривой, а логарифм этого расстояния. Эта спираль пересекает все прямые, проходящие через полюс, под одним и тем же углом.

Первым учёным, открывшим эту удивительную кривую, был Р. Декарт (1596 – 1650г.). Уже в конце XVII в. многие свойства «изумительной спирали» были исследованы Якобом Бернулли.

Золотой прямоугольник (то есть прямоугольник, стороны которого находятся в «золотом отношении») обладает многими необычайными свойствами. Отрезав от золотого прямоугольника квадрат, сторона которого равна меньшей стороне прямоугольника, снова получим золотой прямоугольник меньших размеров. Продолжая отрезать квадраты, будем получать всё меньшие и меньшие золотые прямоугольники.

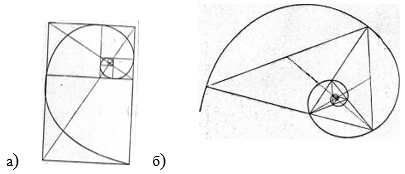
Рисунок 2. Способы вычерчивания логарифмической спирали

(а), делящие стороны прямоугольников в среднем и крайнем отношении, лежат на логарифмической спирали, закручивающейся внутрь. Полюс спирали лежит на пересечении пунктирных диагоналей.

Логарифмическая спираль возникает и во многих других геометрических построениях, связанных с числом «золотое сечение». Один из изящных способов вычерчивания логарифмической спирали основан на использовании равнобедренного треугольника, стороны которого находятся в золотом отношении к основанию (б). Полюс этой спирали лежит на пересечении двух медиан, проведённых пунктиром.

Особенности логарифмической спирали поражали не только математиков. Её геометрические свойства, в частности инвариантность (сохранение угла), удивляет и биологов, которые считают именно эту спираль своего рода стандартом биологических объектов самой разной природы.

ЛОГАРИФМ И БИОЛОГИЯ

Логарифмическая спираль – единственный тип спирали, не меняющей своей формы при увеличении размеров. Это свойство объясняет, почему логарифмическая спираль так часто встречается в природе.

Живые существа обычно растут, сохраняя общее очертание своей формы. При этом они растут чаще всего во всех направлениях – взрослое существо и выше и толще детёныша. Но раковины морских животных могут расти лишь в одном направлении. Чтобы не слишком вытягиваться в длину, им приходиться скручиваться, причём каждый следующий виток подобен предыдущему. Например, по мере роста моллюска Nautilus раковина его, разделённая внутренними перегородками, увеличивается в своих размерах, закручиваясь по логарифмической спирали. При этом домик его не меняет формы: если центральную часть раковины посмотрим под микроскопом, увидим в точности такую же спираль, какая получилась бы, если бы раковина выросла до размеров галактики, и мы разглядывали бы её с большого расстояния. Очертания, выраженные логарифмической спиралью, имеют не только раковины многих моллюсков, улиток, а также рога таких млекопитающих, как архары, в подсолнухе семечки расположены по дугам, также близким к логарифмической спирали, и т. д. По логарифмической спирали формируется и тело циклона. Можно сказать, что спираль является математическим символом соотношения форм роста. Великий немецкий поэт Иоганн Вольфганг Гёте считал её даже математическим символом жизни и духовного развития.

ЛОГАРИФМ «НА СЛУХУ»

Одно из наиболее важных понятий акустики – тон, представляющий собой непосредственное восприятие колебаний, возникающих при звучании струны, человеческого голоса или других источников звука.

Сила звука – это количество звуковой энергии, проходящей через единицу поверхности в единицу времени. Это физическая величина не выражает величины нашего звукового ощущения – громкости. Если будем слушать звуки различных частот, но одинаковой силы, то они покажутся нам отличающимися по громкости. Такое явление объясняется разной чувствительностью нашего уха к звукам различной частоты.

Проведу эксперимент: буду увеличивать силу, какого – ни будь звука в 2, 3, 4 раза и вижу, что моё звуковое ощущение не увеличивается во столько же раз. Оказывается, в 1846 году физиолог Вебер установил зависимость между ощущением и раздражением, вызывающим это ощущение. Им было доказано отношение прироста раздражения к его первоначальной величине всегда остаётся постоянным. Названное отношение можно выразить в процентах. В дальнейшем (в 1860г.) уже другой учёный – Фехнер подверг закон Вебера математической обработке.

По результатам исследования был сформулирован общий психофизический закон Вебера – Фехнера, согласно которому ощущение изменяется пропорционально логарифму раздражения:

Единица измерения децибел используется в звуковой технике.

Связано это с тем, что мы реагируем не на абсолютные, а на относительные изменения уровня какого-либо воздействия, в том числе и звукового.

Если сила звука (интенсивность, I, Вт/м2) изменится в 10 раз, то субъективное ощущение громкости — всего лишь на одну ступеньку, при 100-кратном увеличении силы звука — на две (lg100 = 2), при 1000-кратном — на три (lg1000 = 3). Поэтому увеличение или уменьшение силы звука принято измерять в логарифмических единицах и каждое десятикратное изменение силы звука оценивается единицей, называемой Бел (Б). На практике используется в основном единица, равная десятой части Бела - децибел.

Значение в децибелах равно десяти десятичным логарифмам отношения интенсивностей двух сигналов.

ЛОГАРИФМ И ПСИХОЛОГИЯ.

Ощущения, воспринимаемые органами чувств человека, могут вызываться раздражениями, отличающимися друг от друга во много миллионов и даже миллиардов раз. Удары молота о скользкую плиту в сто раз громче, чем тихий шелест листьев, а яркость вольтовой дуги в триллионы, раз превосходит яркость какой – ни будь слабой звезды, едва видимой на ночном небе. Но никакие физиологические процессы не позволяют дать такого диапазона ощущений. Опыты показали, что организм как бы «логарифмирует» полученные им раздражения, т. е. величина ощущений приблизительно пропорциональна десятичному логарифму величины раздражения. Как видим, логарифмы вторгаются и в область психологии.

ВЫВОД:

Область применения логарифмов весьма разнообразна: математика, литература, биология, психология, сельское хозяйство, музыка, астрономия, физика и т. д. Неспроста великий немецкий поэт Иоганн Вольфганг Гёте считал логарифмическую спираль даже математическим символом жизни и духовного развития. Математика не только формулы, графики, но и логическое объяснение многих явлений, происходящих вокруг нас.

Работая над темой, я раскрыла для себя много интересного, полезного и этим поделилась с Вами.