Определение резонансных частот комплексных колебаний при термосиловой обработке
Журнал: Научный журнал «Студенческий форум» выпуск №23(116)
Рубрика: Технические науки
Научный журнал «Студенческий форум» выпуск №23(116)
Определение резонансных частот комплексных колебаний при термосиловой обработке
DETERMINATION OF RESONANT FREQUENCIES OF A COMPLEX OSCILLATION WITH TERMOLOVO PROCESSING
Eugene Didyk
Student, Togliatti state University, Russia, Togliatti
Voronov Dmitriyv
Candidate of Science, associate Professor, Togliatti state University, Russia, Togliatti
Аннотация. В данной статье представлена математическая модель определения резонансных частот комплексных колебаний при термосиловой обработке маложестких валов. Использование комплексных продольных и крутильных колебаний совместно с термосиловой обработкой позволяет существенно снизить уровень внутренних напряжений в материале маложесткого вала.
Abstract. This article presents a mathematical model for determining the resonant frequencies of complex vibrations in thermosilic processing of low-rigid shafts. The use of complex longitudinal and torsional vibrations in conjunction with thermosilic treatment can significantly reduce the level of internal stresses in the material of a low-rigid shaft.
Ключевые слова: математическое моделирование, термосиловая обработка, комплексные колебания, внутренние напряжения, резонанс, маложесткие валы.
Keywords: mathematical modeling, thermosilic processing, complex vibrations, internal stresses, resonance, low-rigidity shafts.
В работах авторов [1-11] приведены основы автоматизации процесса термосиловой обработки, обоснована необходимость применения комплексных колебаний в сочетании с термосиловой обработкой.
При разработке системы автоматического управления термосиловой обработки (ТСО) с комплексными колебаниями воспользуемся механической моделью процесса ТСО с комплексными колебаниями. Механическая модель комплексных колебаний представляет собой одномассовую модель с двумя степенями свободы. Первая степень свободы – движения вдоль оси х – (∆ х) – обусловлены воздействием на деталь продольной составляющей комплексных колебаний. Вторая степень свободы – движение вокруг оси х на угол – Θ, обусловлено воздействием на деталь крутильной составляющей комплексных колебаний. Математически данная модель описывается системой двух дифференциальных уравнений второго порядка, которые имеют следующий вид (1):
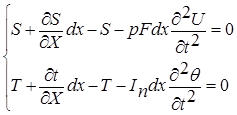(1)
Первое уравнение описывает свободные колебания, второе крутильное. В первом уравнении величина и есть относительное перемещение по оси х: u= ∆х.
Во втором уравнении величина Θ угол поворота вокруг оси х. Данные величины будут иметь наибольшее значение в момент резонанса, т.е. u и ∆х → мах при резонансе по продольным колебаниям, а Θ → мах при резонансе по крутильным колебаниям. Так как при комплексных колебаниях имеет место два резонанса, то условие резонанса напишется как:
Для продольных колебаний частота в условиях резонанса (2):
ωпрi = i×π×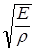 
/L, (2)
Для крутильных колебаний частота в условиях резонанса (3):
ωкрi = i×π×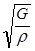 
/L, (3)
Термосиловую обработку с применением комплексных колебаний целесообразно проводить попеременно на резонансных режимах продольных и крутильных колебаний.
На режиме остывания при ТСО проводит уменьшение температуры под воздействием растягивающего усилия. Все это приводит к изменению частот собственных колебаний, и следовательно резонансные частоты смещаются. Это связано со свойствами материала, при повышении температуры значение модулей упругости Е и сдвига – G существенно снижаются, а так же с измерением геометрических параметров изделия, что обусловлено воздействием осевого растягивающего усилия L1= L+∆L. Величины ∆L складывается из комплексного воздействия различных факторов, возникающих при ТСО. Ниже, в формуле (4) показана взаимосвязь данных факторов:
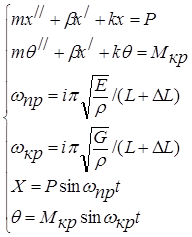, (4)
Из выше сказанного ясно, что для управления данным процессом необходима система автоматического управления. Управляемыми параметрами служат: перемещение по оси х и угол поворота в системе координат х-θ. В момент резонанса значения управляемых параметров будут иметь максимальные значения. Управляющими параметрами служат параметры вынужденных колебаний: амплитуды и частоты продольной и крутильной составляющих комплексных колебаний.
