Диффузион типіндегі бір параметрлі адсорбция мәселесін шешу

РЕШЕНИЕ ОДНОПАРАМЕТРИЧЕСКОЙ ЗАДАЧИ АДСОРБЦИИ ДИФФУЗИОННОГО ТИПА

Кыргызбай Назгуль Сабитовна

Казахский национальный аграрный Университет, Республика Казахстан, г. Алматы

Пирниязова Периуза Мамбетовна

PhD, Казахский национальный аграрный Университет, Республика Казахстан, г. Алматы

Аннотация. Қаралып отырған мақалада бір параметрлі адосрбция мәселесінің диффузион теңдеуінің шешу әдісі қарастырылған, яғни адсорбция мәселесіндегі кинетика бөлігі нөльге теңдеп диффузион теңдеуі шек айрымдылық әдісі мен қарастырылды. Мақалада мәселенің қойылыуы берілген, шек айырымдылық әдісі мен сұлбасы дүзіліп, алынған шек айырымдылық сұлба айдау әдісі мен шешілді.

Мәселенің қойылуы. Мелассаның түйіршікті қабатының ерітіндісінен лимон қышқылын алудың адсорбция процессін қарастырайық.

Сонымен, жылжымалы фаза үшін адсорбцияның бір параметрлі математикалық моделін қарастыратын болсақ, бойлық араластыруды ескере отырып, диффузиялық модельді қолданатын боламыз және осы кезде фазалар арасында жаппай алмасу жүреді. Сонда адсорбция процессінің бір фазалық математикалық моделін келесідей ұсына аламыз, яғни жылжымалы фаза үшін материалдық тепе-теңдік теңдеуі [1]:

                     (1)

Жылжымайтын(қозғалмайтын) фазаның материалдық балансының теңдеуі немесе сорғытылу кинетикасы [1]:

                               (2)

Бастапқы шарттар: .

Шекаралық шарттар:  .

Мұндағы   жылжымалы және қозғалмайтын фазалардағы компоненттердің концентрациясы, г/см³

- сорбаттың тепе-теңдік концентрациясы

координатная ось, длина диффузорного бака, где производится адсорбция, м

t – уақыт, с

D- диффузия коэффициенті, 

v – адсорбцияланатын ағынның көлемдік шығыны, м³/с;

β- пропорционалдылық коэффициенті, кинетикалық коэффициент деп, те аталады, .

Мәселенің шешу әдісі. Шекті айырымдылық әдісінің негізі түсінігі –бұл

теңдеулерді шешуде қолданылатын дискреттеу үздіксіз аймақты оқшауланған нүктелер жиынтығымен (тормен) ауыстыру болып табылады, сонымен қатар, теңдеулерді шешу тек осы нүктелерде (тор түйіндерінде) қарастырылады. Туындыларды шекті айырымдылықтар мен алмастырып, шекті айырымдылық теңдеулерінің шешімі бастапқы есепті шешуге дейін жақындайтын болады. Ол үшін жуықтау қателігі, айырымдылық схемаларының тұрақтылығы мен дәйектілігін талдаймыз. Туындыларды шекті айырымдылық әдісімен жуықтау идеясын жақсы түсіну үшін функциясының  нүктедегі туындысының анықтамасын айтып өтейік [2 ]

Егер функциясы үздіксіз, ал  - жеткілікті аз болса, онда  [ айырымдылық мәні  туындысының мәніне жақын болады.

Айырымдықтың дұрыстығын ресми түрде  - функциясын Тейлор қатары бойынша  ( нүктесіне қойып, туындыларды жуықтау арқылы тексеруге болады.

       (3)

Мұнда x  х х. (3)- формулада «Оң жақтағы айырымдық“ формуласы берілген:

               (4)

туынды жуықтаулар арқылы шексіз көптеген шекті айырымдылықты құруға болады.

        (5)

(5) формулада «Сол жақтағы айырымдық» формуласы берілген:

              (6)

Мысалы, - «оң жақтағы айырымдық“ формуласы мен  «сол жақтағы айырымдық» формулаларының Тейлор қатары бойынша  нүктесінде жайылмасын (4) және (6) қосып, орталық айырмдылық формуласын аламыз[2]:

        (7)

(7) теңдеудегі   – бұл айырымдық сұлбасы, ал қалған  - «туындыны жуықтау қателігі» деп аталады.

Шекті айырымдылық әдісін жартылай дифференциалдық теңдеуді шешуге қолданудағы алғашқы қадамдардың бірі - үздіксіз шекті айырымдылық торына ауысу болып табылады.

  дербес дифференциалдық теңдеуін шешу үшін  аймағын еңгіземіз, Бұл жерде нүктелер жиынтығын торға еңгіземіз (1-сурет)[2], мұндағы  бүтін сандар.  

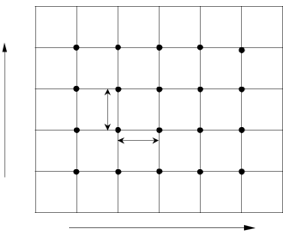
Сурет 1. Шекті айырымдылқтың торда берілу

Шекті айырымдылықтың торда берілу мысалы және шамаларының мәндері арқылы тор ішіндегі нүктелердің орналасуы анықталады, сондықтан да айырымдылық теңдеулері әдетте еркін түйін үшін жазылады ).

 емес,  () –ді қарастыратын боламыз (қысқартылған түрде -). Осы жазбаға сәйкес (3), (4) және (5) өрнектер келесідей түрде жазылады[3-5]:

                     (8)

Жақындау қателігін  -формада көрсету, абсолюттік шамадағы жуықтау қателігі -   ге ұмтылатуғын білдіреді. Мұндағы  – тұрақты сан.

Дәл осындай етіп, - айнымалысы бойынша туындыны келесі түрде жазуға болады:

                 (9)

Әрбір дербес дифференциалдық теңдеу үшін оның көптеген айырымдық сұлбалары бар, олардың ішінен әдетте барлық көзқарастар бойынша ең жақсысын таңдау қиынға соғады. Біріншіден, шекті айырмдылықтар әдісін қолданғанда, қойылған есеп теңдеулерін дұрыс жақындатуға ұмтылу керек, екіншіден, «ең жақсы» схеманы таңдап алу керек, яғни оның дәлдігін, тиімділігін ескере отырып оңтайландыру керек және бағдарламалық қамтамасыздандыруды компьютерде жүзеге асырудың ыңғайлылығын қарастырған жөн. Жоғарыда қарап өткендей берілген теңдеудің сұлбасын төмендегіше аламыз, біртекті мәселесін қарастыралық, яғни   . Онда біз диффузия теңдеуін аламыз

белгілерді еңгіземіз , а    , және жоғарыда алынған сұлбаларды орнына (1) теңдеуіне қойып келесі түрге келтіреміз[2,4,7]:

      (10)

Бастапқы шарт : 

Шекаралық шарттар: 

(10) теңдеуге белгілеулер кірітіп, яғни   төмендегі түрге келеміз

      (11)

(11)теңдеуді шешу ұшін сандық әдістердің «Айдау әдісін» қолданамыз. Бұл жерде (11) теңдеуді түрлендіріп төмендегі түрге келтіреміз

      (12)

Белгілеулер кірітеміз

;   (13)

Белгілеулер кірітеміз, яғни   

 ;  ;  ;

Сонымен қатар (13) теңдеудің және (1) тендеудің жалпы шешімі төмендегі көріністе болады

   (14)

Жоғарыда койылған мәселенің (1.2) аналитикалық шешімі n=5 дейінгі қабатында, ал торларды m= 5 торына дейін қарастырылды.