Расчеты задач по физике с помощи МС Exsel

Введение

В статье рассматривается способ повышения качества образовательного процесса в морском ВУЗе, который предусматривает использование новейших компьютерных технологий при решении задач по физике. На примере данной работы представим способ решения задачи с помощью MS Excel , она производит расчеты, позволяет строить графики и анализировать данную задачу.

Пример практической задачи: Парашютист при падении на землю испытывает действие силы тяжести (mg) и силы сопротивления воздух (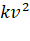 ),где k- это коэффициент сопротивления. Необходимо определить коэффициент сопротивления k, чтобы парашютист приземлялся со скоростью не более 8 м/сек, не представляющей опасности для жизни и здоровья

Таблица

Данные

Ход работы:

В рассматриваемых ниже физических задачах фундаментальную роль играет второй закон Ньютона. Он гласит, что ускорение, с которым движется тело, прямо пропорционально действующей на него силе (если их несколько, то равнодействующей, т.е. векторной сумме сил) и обратно пропорционально его массе:

mа = mg — kV²                                                                                                                     (1)

Рисунок 1. Иллюстрация к задаче

Из уравнения (1) выразим ускорение:

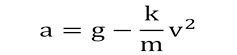                                                                                     (2)

Будем также считать, что на каждом промежутке ускорение постоянно и равно а_i. Формула для вычисления ускорения имеет вид:

                                                                                      (3)

Но для MS Excel такой вид формулы будет не понятен. Для MS Excel формула будет иметь вид:

$A9-(($B9/$C9)*($D9^2))

Где А9, В9, С9, D9 – название ячейки

$ - закрепление столбца или строчки ( зависит от того, где стоит знак : перед буквой – столбца, перед цифрой – строчки)

Таблица 2

Расчёты

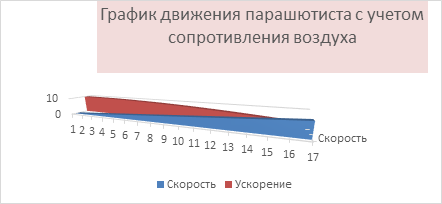
Рисунок 2. График

Скорость в конце промежутка (и, соответственно, в начале следующего) вычисляется по формуле равноускоренного движения:

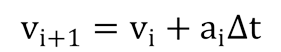                                                                                       (4)

Расстояние, которое пролетел парашютист, равно сумме расстояния, пройденного к началу очередного промежутка времени (S_i), и расстояния, пройденного на этом промежутке:

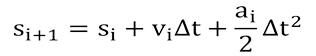                                                                                 (5)

Соответственно для MS Excel формула имеет вид :

($G7*$I7)+($H7/2*($I7^2))

Таблица 3

Данные

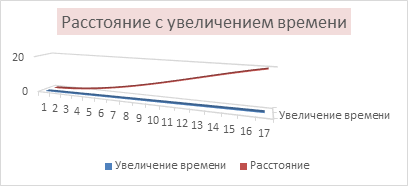
Рисунок 3. Расстояние с увеличением времени

Вывод:

Таким образом, с помощью программы MS Excel мы смогли определить такой коэффициент сопротивления k, чтобы парашютист приземлялся со скоростью не более 8 м/сек которая в свою очередь не представляющей опасности для жизни и здоровья.

Так же мы проанализировали зависимость коэффициента сопротивления воздуха от скорости движения парашютиста.  

Приведенный способ способен значительно повысить уровень знаний по физике с помощи применения компьютерный программ.