Обоснование угла наклона ударной поверхности била

JUSTIFICATION OF THE ANGLE OF INCLINATION OF THE IMPACT SURFACE OF THE BILL

Ferzulla Ferzullaev

Student, Saratov State Technical University them Gagarina Yu.A., Russia, Saratov

Ivan Pavlov

dr. tech. sciences, professor, Saratov State Technical University them Gagarina Yu.A., Russia, Saratov

Аннотация. Проведены расчеты по определению кинематических показателей молотковой мельницы. Выполнено обоснование угла наклона ударной поверхности била.

Abstract. Calculations are carried out to determine the kinematic parameters of the hammer mill. Justification of the angle of inclination of the impact surface of the bill is performed.

Ключевые слова: Молотковая мельница, било, угол наклона била.

Keywords: Hammer mill, bilo, the angle of inclination of the bilo.

В молотковых мельницах рабочий орган – било – относится к быстро изнашивающимся элементам конструкции. Низкий срок их службы снижает эффективность мельниц, ведет к увеличению количества технических обслуживаний, повышению расхода оборотных средств на обслуживание оборудования. Повышение эффективности использования мельниц возможно увеличением срока службы молотков до их предельного состояния и межремонтного периода.

В процессе работы в результате периодических ударов об измельчающий материал, например, каменный уголь, било отклоняется от своего радиально-равновесного состояния на некоторый угол. Сила удара угля о молоток раскладывается на две составляющие: нормальную, в основном дробящую уголь, и касательную, способствующую проскальзыванию угля по молотку, что приводит к износу. Для исключения проскальзывания материала по молотку необходимо исключить или компенсировать угол его отклонения.  

Проведем динамическое исследование частицы материала, перемещающейся по участкам загрузочной камеры, с помощью задачи динамики. Для определения абсолютной скорости частицы при взаимодействии с билом определим скорость ее перемещения в загрузочной камере и окружную скорость била.

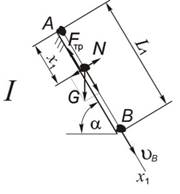
Кусок угля (примем за материальное тело) движется из точки A по участку I длиной L₁ (рисунок 1) по наклонной плоскости загрузочной камеры, составляющей угол α с горизонтом. Начальная скорость тела υ₀. Коэффициент трения скольжения тела по плоскости − f. В точке В тело покидает плоскость со скоростью υ_В.

Рассмотрим движение тела на прямолинейном участке АВ. Тело примем за материальную точку.

Изобразим материальную точку в трех положениях: начальном – в точке А (см. рисунок 1, а), промежуточном и конечном – в точке В. В начальном и конечном положениях покажем векторы скорости, а в промежуточном – все активные силы и реакции связи. На точку действует одна активная сила – сила тяжести G  Под действием активной нагрузки в месте контакта материальной точки с опорной поверхностью возникает реакция опоры – N, направленная перпендикулярно опорной поверхности в направлении, противоположном тому, в котором связь препятствует перемещению тела в пространстве. Так как присутствует коэффициент трения , то на материальную точку также действует и сила сопротивления движению F_тр, которая направлена противоположно вектору скорости тела.

Выберем систему координат. На участке АВ материальная точка движется по прямолинейной траектории, поэтому для решения задачи необходимо и достаточно одной координатной оси – Ах₁, начало которой совпадает с точкой начала движения − А, а направление − с вектором начальной скорости – υ₀.

Выбрав начальные и конечные условия (; ; ; ; ; ), скорость точки записываем в проекции на выбранную систему координат.

Составим дифференциальные уравнения движения материальной точки на участке АВ. Запишем основное уравнение динамики для рассматриваемых условий

.                                            (1)

Спроецируем данное выражение на координатную ось − 

                                            (2)

где , , а .

Подставив, получим

                              (3)

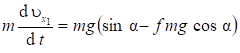.                                    (4)

Сократим на массу m.

Разделив переменные и проинтегрировав, получим

.                                  (5)

Из кинематики известно, что , тогда выражение (5) примет вид

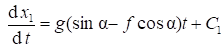.                                    (6)

Разделим переменные и проинтегрируем

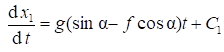|                            (7)

.                                   (8)

Используя начальные условия, определим постоянные интегрирования

;  .

Подставив полученные значения  и  в выражения (5) и (8), получим

.                                       (8)

.                                       (9)

Используя конечные условия, определим искомые величины

Из выражения (9)

                                       (10)

Время движения тела на участке АВ

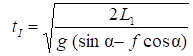                                       (11)

,                                              (12)

где  – скорость точки в любой момент времени, м/c.

,                                              (13)

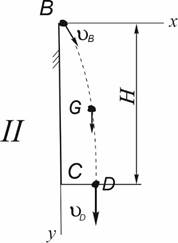
Рассмотрим движение тела на криволинейном участке траектории ВD. Тело движется в вертикальном направлении в течение t₂ с под действием силы тяжести G. Начальная скорость тела υ₀ = υ_В =.

Изобразим материальное тело в трех положениях: начальном – в точке В, промежуточном – в точке С и конечном – в точке D (рисунок 1, б). В начальном и конечном положениях покажем векторы скорости, а в промежуточном – все активные силы. Сопротивлением воздуха пренебрегаем. На точку действует одна активная сила – сила тяжести G.

Так как на участке ВD материальная точка движется по криволинейной траектории, то для решения задачи необходимы две координатные оси. Выберем систему координат − , начало которой совпадает с точкой − В, а направление осей выбираем таким образом, чтобы проекция на них вектора  была положительной величиной.

Запишем начальные и конечные условия (начальные условия: ; ; ; ; конечные условия: ), причем скорость точки записываем в проекциях на выбранную систему координат − .

Составим дифференциальные уравнения движения материальной точки на участке ВD. Запишем основное уравнение динамики

.

Спроецируем данное выражение на координатную ось − :

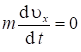, так как , то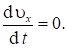 

Разделим переменные

|   ,                             (14)

и проинтегрируем

.                                                     (15)

Из кинематики известно, что , тогда выражение (15) примет вид

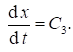
Разделим переменные и интегрируем

|

.                                                (16)

Спроецируем выражение движения материальной точки на участке ВD на координатную ось :

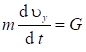, так как , то 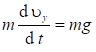, на массу можно сократить.

Разделим переменные и интегрируем

|   

.                                                (17)

Из кинематики 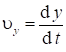. Тогда выражение (17) примет вид

Разделим переменные и интегрируем

|

.                                             (18)

Используя начальные условия, определим постоянные интегрирования

;  ;  ;  .

Подставим полученные значения – в выражения (15) – (18), получим

,                                       (19)

,                                        (20)

,                                      (21)

.                                   (22)

Используя конечные условия, определим время перемещения тела.

Из выражения (19)

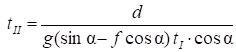,                                    (23)

где 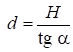 следует из схемы;− из выражения (22).

Тогда

.

Подставив время перемещения тела в выражение (21), получим выражение его скорости при соударении с билом 

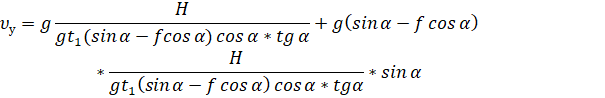
Угловая скорость ротора определяется по выражению

где R – радиус ротора мельницы, м; – частота вращения ротора, .

Окружная скорость торца била

.

Результирующая скорость взаимодействия частицы материала с билом определяется выражением

,

Угол наклона β результирующей скорости υ_р

.

Вывод. Величина угла β определяет потребный наклон ударной поверхности била, который сводит трение тела по поверхности била к минимуму и повысит его ресурс.