МЕТОД МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ

METHOD OF MATHEMATICAL INDUCTION

Djamilya Evloeva

Student Ingush State University, Russia, Magas

Fatima Tsurova

Research Supervisor, Associate Professor of the Department of Mathematical Analysis, Ingush State University, Russia, Magas

Аннотация.  Ппредметом исследования является эффективное использование метода математической индукции, математического доказательства, который используется, чтобы доказать истинность некоторого утверждения для всех натуральных чисел. Универсальным методом доказательства является метод математической индукции. Можно сравнить метод математической индукции с прогрессом, в котором мы начинаем с низшего, в результате логического мышления приходим к более высшему.

Abstract. the subject of the study is the effective use of the method of mathematical induction, a mathematical proof that is used to prove the truth of some statement for all natural numbers. The universal method of proof is the method of mathematical induction. We can compare the method of mathematical induction with progress, in which we start from the lowest, as a result of logical thinking we come to a higher one

Ключевые слова: индукция, полная индукция, неполная индукция,  математическая индукция, метод доказательства ,дедукция, дедуктивный метод, анализ ,аксиома, тождество, сравнение, повторение, рассуждение.

Keywords: induction, full induction, incomplete induction, mathematical induction, proof method ,deduction, deductive method, analysis,axiom, identity, comparison, repetition, reasoning.

В процессе было выяснено, что все утверждения можно разделить на общие и частные. Примером общего утверждения является, например, утверждение: «В любом треугольнике сумма двух сторон больше третьей стороны». Частным является, к примеру, утверждение: «Число 136 делится на 2».

Переход от общих утверждений к частным называется дедукцией. В математике дедуктивный метод мы применяем, например, в рассуждениях такого типа: данная фигура – прямоугольник; у каждого прямоугольника диагонали равны, следовательно, и у данного прямоугольника диагонали равны.

Но наряду с этим математике часто приходится от частных утверждений переходить к общим, т.е. использовать метод, противоположный дедуктивному, который называется индукцией.

В математике роль индукции в значительной степени состоит в том, что она лежит в основе выбираемой аксиоматики. После того как длительная практика показала, что прямой путь всегда короче кривого или ломанного, естественно было сформулировать аксиому: для любых трех точек А, В и С выполняется неравенство.

Принцип математической индукции.

Утверждение Р(п), зависящее от натурального п, справедливо при всех натуральных п, если

1) доказана справедливость утверждения при п=1;

2) из предположения справедливости утверждения Р(п) при п=к следует

справедливость Р(п) при п=к+1.

В математике принцип математической индукции выбирается, как правило, в качестве одной из аксиом, определяющих натуральный ряд чисел, и, следовательно, принимается без доказательства. Метод доказательства по принципу математической индукции обычно называется методом математической индукции. Заметим, что этот метод широко применяется при доказательстве теорем, тождеств, неравенств при решении задач на делимость и многих других задач.

Полная и неполная индукция.

В случае, когда математическое утверждение касается конечного числа объектов, его можно доказать, проверяя для каждого объекта, например, утверждение «Каждое двузначное четное число является суммой двух простых чисел». Метод доказательства, при котором мы проверяем утверждение для конечного числа случаев, называется полной математической индукцией. Этот метод применим сравнительно редко, так как утверждения чаще всего рассматриваются на бесконечных множествах. Например, теорема «Любое четное число равно сумме двух простых чисел» до сих пор ни доказана, ни опровергнута. Если бы мы даже проверили эту теорему для первого миллиарда, это бы ни на шаг не приблизило бы нас к её доказательству.

В естественных науках применяют неполную индукцию, проверяя эксперимент несколько раз, переносят результат на все случаи.

Пример № 1.

Угадаем с помощью неполной индукции формулу для суммы кубов натуральных чисел.

Решение.

1³=1; 1³+2³=(1+2)²; 1³+2³+3³=(1+2+3)²; 1³+2³+3³+4³=(1+2+3+4)²;

1³+2³+3³+4³+5³=(1+2+3+4+5)²; …; 1³+2³+…+n³=(1+2+…+n)².

Доказательство.

Пусть верно для п=к. 

Докажем, что верно для п=к+1.

Вывод: формула для суммы кубов натуральных чисел верна для любого натурального п.

Пример № 2.

Запишите в виде суммы следующие выражения:

1)  2)  3); 4) .

греческая буква «сигма».

Пример № 4.

Запишите следующие суммы с помощью знака :

1)

2) 

Доказательство тождеств методом математической индукции.

Метод математической индукции позволяет доказывать различные тождества.

Пример № 5. Докажем, что для всех п выполняется тождество

Решение.

Положим

Нам надо доказать, что 

Докажем, что  Тогда из истинности тождества следует истинность тождества 

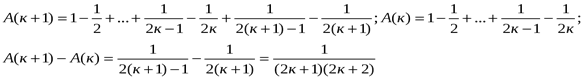
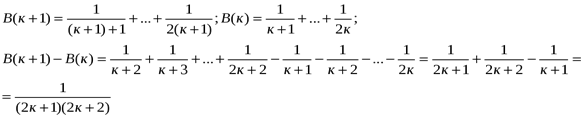
По принципу математической индукции доказана истинность тождества при всех п.

Вывод: В ходе работы я узнала, чтобы решать задачи методом математической индукции нужно знать и понимать основной принцип математической индукции.

Достоинством метода математической индукции является его универсальность, так как с помощью этого метода можно решить многие задачи. Недостатком неполной индукции является то, что порой она приводит к ошибочным выводам.

Так же в ходе работы приобрела навыки решения задач по использованию метода математической индукции. Считаю, что эти навыки помогут мне в будущем.