Теория бесконечных определителей

Идея введения определителей восходит к известному немецкому математику Готфриду Вильгельму Лейбницу (1646–1716). Лейбниц пришел к определителям при решении систем линейных уравнений в 1678 году. К сожалению, Лейбницем в 1700 году был опубликован лишь метод обозначения коэффициентов без каких-либо практических приложений и выводов, поэтому открытие определителей прошло практически незамеченным.

В 1750 году определители были вновь изобретены женевским математиком Крамером. Метод Крамера был замечен и очень скоро стал основной частью школьной программы.

Первые полные изложения теории принадлежат Бине и французскому математику Огюстену Коши(1789–1857). Бине и Коши одновременно занялись теорией определителей, и получили некоторые общие результаты. Коши посвятил теории определителей еще 14 мемуаров. Именно он совсем близко подошел к современному обозначению элементов определителя, употребляя запись .

Бесконечной системой линейных алгебраических уравнений с бесконечным множеством неизвестных называется система уравнений:

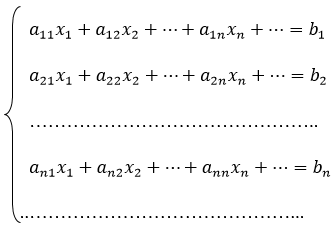                                                                                     (1)

где   – известные коэффициенты,   – свободные члены и     –неизвестные из поля F.

Совокупность численных значений величин    называется решением системы (1), если после подстановки этих значений в левую часть равенств (1),  мы получим сходящиеся ряды,  и все эти равенства будут удовлетворены, в противном случае система не имеет решений.

В случае разрешимости бесконечная система называется совместной, в противном случае – несовместной.

Под бесконечной матрицей А понимаем таблицу коэффициентов бесконечной системы (1):

которая называется матрицей системы (1). Кроме того, рассматривается расширенная матрица А:

Выделив элементы, содержащиеся в первых  n  столбцах и первых n строках матрицы,  образуем из них определитель  n-го  порядка . Его называют главным определителем  n-го  порядка, порождаемого матрицей  А.

Если при неограниченном возрастании порядка n главного определителя  матрицы  А  его значение стремится к определённому пределу  , то существует бесконечный определитель, образуемый матрицей А, и  что  есть значение этого определителя.

Пусть вместо бесконечной системы (1) задана общая конечная система m линейных алгебраических уравнений с n неизвестными, тогда основная матрица А будет размера n на m , а расширенная прямоугольная матрица  с размерами   .

Приведём теорему Кронекера-Капелли для конечных систем в расширенном варианте в терминах ранга матрицы.

Теорема 1 (Кронекера-Капелли). Для того, чтобы конечная система уравнений имела решение, необходимо и достаточно, чтобы ранг расширенной матрицы был равен рангу основной матрицы этой системы. Если ранги основной и расширенной матриц совпадают с числом неизвестных, то система имеет единственное решение. Если ранг r основной и расширенной матриц меньше числа n неизвестных, то конечная система имеет более одного решения. Размерность подпространства решений однородной конечной системы линейных уравнений с n неизвестными равна   матрицы,   декремент  основной матрицы системы.

Из бесконечной матрицы A выделим k строк и k столбцов соответственно с номерами  .  Из элементов, стоящих на пересечении этих строк и столбцов, не меняя их порядка, составим определитель. Это определитель k-го порядка, порождаемый исходной матрицей, т. е. является минором k-го порядка бесконечного определителя |A| в случае  его существования. Такого рода минор будем обозначать символом  . Элементы  мы можем рассматривать как миноры первого порядка бесконечного определителя |A|.

Бесконечная матрица A вида (2) может иметь определенный ранг.  Именно   если из определителей k-го порядка, порождаемых матрицей, хотя бы один отличен от нуля, а определители k+1-го порядка все равны нулю, то эта матрица имеет k-ый  ранг. Если эта матрица порождает бесконечный определитель |A|, то тот же ранг присваивается и определителю |A|. Таким образом, можно сказать, что бесконечный определитель имеет k-ый ранг, если среди его миноров  k-го порядка есть хотя бы один, отличный от нуля, а  его миноры k+1-го порядка все равны нулю.

Совершенно  ясно, что в определителе k-го ранга всякий минор, порядок которого выше k-го, равен нулю.

Теорема 2. Если бесконечная матрица A вида (2) имеет k-ый ранг, то существует порожденный ею бесконечный определитель, и значение его равно нулю.

Доказательство. При  все главные определители  равны нулю, а потому и   .

Теорему 2 можно переписать  следующим образом:

Теорема 2’. Всякий бесконечный определитель конечного ранга равен нулю.

Отсюда следует, что бесконечный определитель, имеющий значение, отличное от нуля, не имеет конечного ранга. Этому  выводу, который легко получить   непосредственно, можно дать следующую  формулировку.

Теорема 3. Если бесконечный определитель имеет значение, отличное от нуля, то среди его миноров k-го порядка есть хотя бы один, отличный от нуля, каково бы ни было целое число k.

Таким  образом, бесконечная матрица в основном не имеет конечного ранга, она  может иметь конечный ранг только тогда, когда её определитель равен нулю, и то не  всегда. Следовательно, использование понятия ранга матрицы для получения результатов, подобных теореме Кронекера-Капелли для бесконечных систем, теряет смысл. Поэтому  как и в теореме 1’ необходимо ввести другое понятие – понятие декремента бесконечной матрицы.

Понятие декремента минора бесконечного определителя |A| и понятие декремента самого определителя |A| (или матрицы A) – это разные  понятия.

В матрице бесконечного определителя |A| опустим столбцы с номерами   и строки с номерами . Остающаяся бесконечная матрица может дать бесконечный определитель,  а может его и не дать. 

Если матрица, которая получается из матрицы бесконечного определителя |A| путем устранения столбцов  и  строк , порождает бесконечный определитель, то последний называется бесконечным минором определителя |A|, а число k называется декрементом этого минора. Этот минор обозначается через . Произведение этого минора на , где  ,   называется алгебраическим дополнением минора k-го порядка   и обозначается через, так что

О минорах бесконечного определителя

Пусть  есть главный определитель n-го порядка бесконечного определителя Δ. Если составим минор k-го порядка определителя , взяв для этого  столбцов   и   строк,  то он совпадет с минором   определителя. Но их алгебраические дополнения будут  различны: в определителе это алгебраическое дополнение представляет собой  определитель -го порядка, в определителе Δ это алгебраическое дополнение может и  вовсе не существовать, а если оно существует, то представляет собой бесконечный определитель.  Алгебраическое       дополнение минора  в определителе обозначим через 

Теорема 4. Если в бесконечном определителе Δ существует алгебраическое дополнение минора , то оно представляет собой предел, к которому  стремится алгебраическое дополнение того же минора в определителе , когда n неограниченно возрастает, т. е.

 .

Теорема 5.  Если в бесконечном определителе Δ все элементы столбцов  равны нулю, кроме тех, которые принадлежат минору k-го порядка    (или если равны нулю все элементы строк, кроме тех, которые принадлежат тому же минору), а сам минор  отличен от нуля, то существует дополнительный минор

  и .

Теорема 6. Если в бесконечном определителе Δ существует алгебраическое дополнение    минора k-го порядка   то оно равно значению, которое примет определитель Δ, если в нем в столбцах  (или в строках заменить нулями все элементы, кроме тех, которые занимают диагональные места в миноре  а диагональные элементы этого минора заменить единицами).

Пусть матрица A системы (1) имеет декремент, равный нулю, т. е. матрица (2) порождает бесконечный определитель, отличный от нуля. Следовательно, на

основании теорем 2 и 2’ матрица (2) имеет бесконечный ранг. Тогда справедливо преобразование Гаусса: A=BC, где B – треугольная, C – гауссова матрицы [15]. Таким образом, вместо общей системы (1) мы можем рассмотреть бесконечную гауссову систему:

где  – коэффициенты соответствующей гауссовой матрицы C,  –    вектор-столбец матрицы ,  – вектор-столбец свободных членов системы (1), – обратная матрица треугольной матрицы B. Частное решение системы (5), которое можно получить методом редукции в узком смысле [1-2] (методом простой редукции), названо строго частным решением системы (5) [3-4]. Оказалось, что строго частное решение играет огромную роль в теории бесконечных систем линейных алгебраических уравнений, в частности, получена основная теорема [3-4]:

Теорема 7. Неоднородная гауссова система (5) совместна тогда и только тогда, когда существует ее строго частное решение.

Теорема 8. Пусть бесконечная неоднородная система (1) является совместной, кроме того, декремент основной матрицы A равен нулю. Тогда неоднородная система (1) имеет строго частное решение, которое имеет вид:

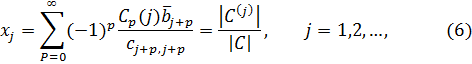
где   определители порядка p, рекуррентно определяемые соотношением:

Здесь определитель гауссовой матрицы С, в которой    столбец заменён столбцом свободных членов  системы (5).

Теорема 9. Пусть выполняются условия теоремы 8.Тогда справедливы соотношения:

где    – определитель матрицы A общей системы (1), в которой j-й столбец заменен столбцом свободных членов системы (1), – определитель гауссовой матрицы C, в которой j-й столбец заменен столбцом свободных членов  системы (5), т. е. столбцом матрицы  – вектор-столбец свободных членов системы (1).

Теорема 10. Пусть выполняются условия теоремы (8). Тогда неоднородная система (1) имеет единственное частное решение, которое определяется формулой Крамера – это строго частное решение системы (1):

где – определитель  , в котором j-й столбец заменен столбцом свободных членов системы (1).

Лемма. Необходимым условием существования решения неоднородной бесконечной системы (1) является выполнение для матриц  системы (1) следующих условий:

1) существуют бесконечные определители  и , порождаемые соответственно матрицей A и расширенной матрицей ;

2) существуют бесконечные миноры  и    соответственно определителей ;

3) над матрицами  осуществляются только допустимые действия.

Теорема 11. Тривиальное решение однородной гауссовой системы (5) является ее строго частным решением.

Теорема 12. Пусть декремент матрицы A равен нулю и если этот декремент повышается с присоединением столбца свободных членов неоднородной системы (1), то бесконечная система (1) несовместна.

Теорема 13. Пусть декремент матрицы A системы (1) равен нулю. Если в выражении (6) ряд не сходится при некотором , тогда система (5) несовместна.