Анализ методов оптимизации транспортной задачи

Введение

На протяжении  всей второй половины двадцатого века появляется обширный  ряд областей математики, в наименование которых входит слово программирование: линейное программирование, нелинейное программирование, динамическое программирование, дискретное программирование, стохастическое программирование и т.д. Комплекс данных дисциплин нередко принято объединять единым термином математическое программирование. Именно задачи линейного программирования были первыми основательно изученными задачами оптимизации при существовании ограничений типа неравенств. Общая задача линейного программирования – это необходимость поиска максимума или минимума функции, называемой функцией цели, при ограничениях, заданных системой уравнений или линейных неравенств.

Задачи линейного программирования очень глубоко и основательно вошли в нашу повседневную жизнь. Одна из разновидностей задач линейного программирования – транспортная задача. Её можно рассматривать как задачу об оптимальном плане перевозок грузов из пунктов отправления в пункты назначения, с минимальной суммарной стоимостью перевозки.

Существует ряд методов построения опорного плана при решении такого рода задач: метод Минимального элемента, метод Северно-Западного угла, метод Аппроксимации Фогеля, метод Двойного предпочтения. Также имеются два метода оптимизации опорного плана: метод потенциалов и распределительный метод.

Общий алгоритм решения классической транспортной задачи

Первым делом при решении транспортной задачи необходимо определить, какой тип имеет задача. Она может быть как открытая, так и закрытая. Если сумма объёма продукта равна сумме объёма потребности, то задача является задачей закрытого типа. В противном случае -  открытого типа.

Далее, на втором этапе, используя один из методов нахождения опорного плана, получаем допустимое решение задачи, которое не всегда оптимальное. Затем находим опорное решение транспортной задачи.

Опорным решением транспортной задачи будем называть любое допустимое решение, для которого векторы условий, соответствующие положительным координатам, являются линейно независимыми.

Для проверки линейной независимости векторов условий, соответствующих положительным координатам для допустимого решения, применяются циклы. Циклом называется ряд клеток таблицы задачи, в которой две рядом стоящие клетки находятся в одном столбце или строке, причем первая и последняя также находятся в одном столбце или же строке. Система векторов условий является линейно независима только в том случае, когда из соответствующих им клеток таблицы невозможно создать ни одного цикла.

Последний этап решения транспортной задачи состоит в усовершенствовании найденного опорного плана. На данном этапе используют распределительный метод или метод потенциалов. На этом этапе точность решения можно соблюдать через функцию стоимости. Если она уменьшается (при условии, что затраты уменьшаются), то ход решения задачи является верным.

Цель работы

Цель работы – программная реализация и сравнение распределительного метода и метода потенциалов при решении транспортной задачи, выявление достоинств и недостатков каждого из методов.

Распределительный метод состоит в поиске оценок циклов пересчета для каждой незанятой клетки таблицы. В случае если оценка цикла не положительна, то решение задачи можно усовершенствовать благодаря переносу перевозки x_ij по циклу. В случае если все оценки циклов положительны, решение – оптимально. Стоимость транспортировки единицы груза из каждого пункта отправления в необходимые пункты назначения задаётся матрицей тарифов. Первоначально отыскивается какое-то решение задачи - начальный опорный план. Затем с использованием специальных показателей опорный план тестируется на оптимальность.

В случае не оптимальности плана, переходят к следующему плану.

Притом последующие планы должны быть лучше предыдущих.

Таким образом за несколько постепенных переходов от не оптимального плана приходят к оптимальному.

Метод потенциалов – это усовершенствованный вид распределительного метода. Он более практичен для решения транспортных задач.

Сущность данного метода заключается в том, что для каждого столбца и каждой строки таблицы определяются потенциалы, при помощи которых устанавливается необходимость наполнения пустых клеток. Потенциалы определяются по заполненным клеткам. Элемент таблицы равен сумме потенциалов столбца и строки, на пересечении которых эта клетка находится: С_ij = U_i + V_j

Изначально первый потенциал для строки U_i или столбца V_j берётся равным нулю, остальные же вычисляются с помощью элементов непустых клеток:

• потенциал строки U_i = C_ij - V_j,
• столбца V_j = C_ij - U_i.

Для решения задачи методом потенциалов изначальный план должен иметь число заполненных клеток m+n-1, расположенных в порядке вычеркиваемой комбинации.

Программная реализация

Для анализа временных затрат на исследуемые методы оптимизации нами была разработана программа на С# с применением Windows Forms. Наша программа сначала считывает данные из файла и заполняет таблицы. Таблица А содержит данные по запасам груза на складах, таблица MatrB содержит данные по потребностям заказчиков и таблица A_i x B_i содержит данные по стоимостям перевозок продукции одной машиной от складов к заказчикам (см. рисунок 1).

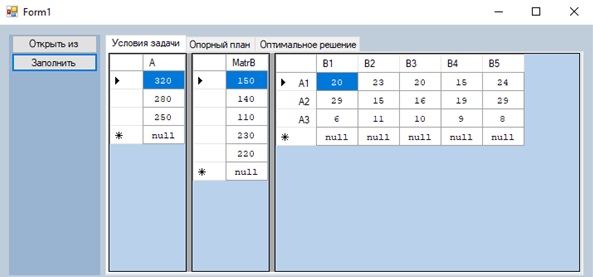
Рисунок 1. Ввод данных

После этого мы строим опорный план методом Северо-Западного угла (см. рисунок 2).

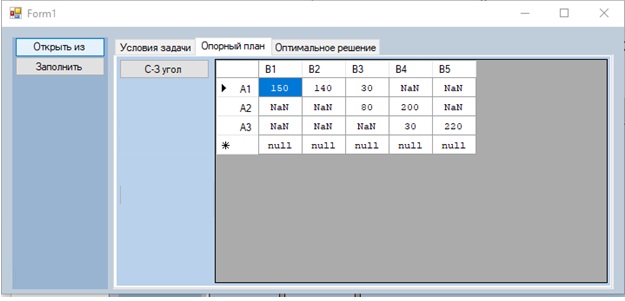
Рисунок 2. Нахождение опорного плана

И затем находим оптимальное решение одним из методов оптимизации и рассчитываем минимальную стоимость (см. рисунок 3).

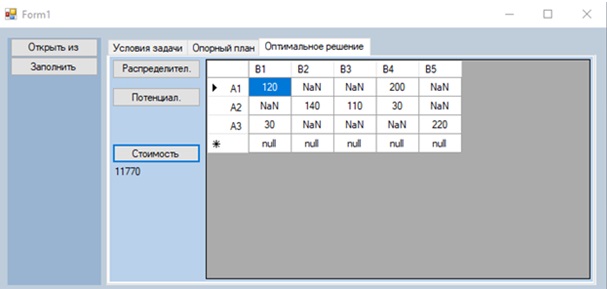
Рисунок 3. Минимальный план перевозок

Для анализа временных затрат рассматриваемых методов оптимизации мы взяли различные размеры таблиц при постановке транспортной задачи и проанализировали полученные данные. Результаты нашей работы можно увидеть в Таблице 1 и на Рисунке 4.

Таблица 1.

Время работы распределительного метода и метода потенциалов

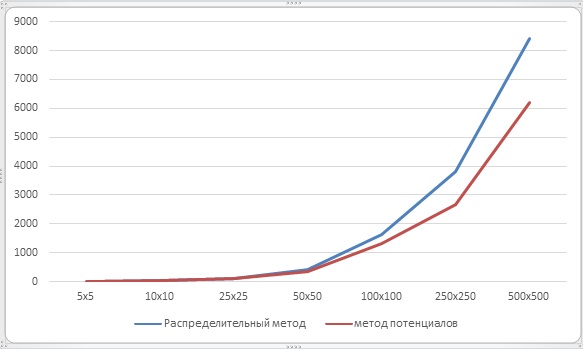
Рисунок 4. Время работы распределительного метода и метода потенциалов

Заключение

Метод потенциалов - широко применяемый метод для решения транспортных задач. Он позволяет облегчить наиболее сложный фрагмент вычислений, а именно нахождение оценок свободных клеток. В ходе анализа были выявлены достоинства и недостатки данного метода оптимизации. Достоинства: искать циклы с отрицательной ценой не нужно, довольно быстро определяет оптимальный план.

Недостатки: при использовании метода нужно иметь допустимый опорный план, полученный каким-то способом. Систему потенциалов можно построить только для случая невырожденного опорного плана. Такой план содержит m + n -1 непустых клеток, поэтому для него можно составить систему из m+n-1 линейно независимых уравнений вида с m + n неизвестными. Уравнений на одно меньше, чем неизвестных, поэтому система является неопределенной и одному из неизвестных присваивают нулевое значение.

Далее остальные потенциалы определяются однозначно.

Распределительный метод состоит в постепенном усовершенствовании опорного плана перевозок путем нахождения на каждом этапе выгодных циклов переноса грузов.

Достоинством метода безусловно является простота алгоритма. Недостатком является то, что нужно отыскивать циклы для всех пустых клеток и находить их цены.

В результате нашего исследования мы выяснили, что метод потенциалов занимает меньше времени, чем распределительный. Это объясняется тем, что метод потенциалов был основан на распределительном методе и учитывает некоторые его недостатки.