Решение задачи краевой раскраски графа

Введение

Теория графов — раздел дискретной математики, изучающий свойства графов.

Основателем теории графов считается Леонард Эйлер. Он в 1736 сформулировал и предложил решение задачи, впоследствии ставшей классической задачей теории графов. Это была задача о 7 кёнигсберских мостах. В этой математической задаче спрашивалось, как можно пройти по всем 7-ми мостам немецкого города Кёнигсберг, не проходя ни по одному из них дважды. Это оказалось невозможно, таким образом были изобретены эйлеровы циклы.

Термин «граф» впервые был введен Джеймсом Джозефом Сильвестром в 1878 году в своей статье в журнале Nature.

В общем смысле граф представляет собой множество вершин, так же называемых узлами, соединённых рёбрами. Но также существует строгое определение понятия граф. Итак, граф – это  такая пара множеств G=(V,E), где V – это подмножество любого счетного множества, а E – подмножество декартового произведения V×V [1].

Теория графов на сегодняшний день находит применение во многих сферах жизни: в информатике и программировании (автоматы, граф-схемы), в химии (описание структур, путей сложных реакций, правило фаз также может быть интерпретировано как задача теории графов), в коммуникационных и транспортных системах (маршрутизация данных в Интернете), в компьютерной химии (точное определение числа теоретически возможных изомеров углеводородов и других органических соединений), в экономике, в логистике, в схемотехнике (топология межсоединений элементов на печатной плате или микросхеме представляет собой граф или гиперграф), в геоинформационных системах (дома, сооружения и т. п. рассматриваются как вершины, а соединяющие их дороги, инженерные сети и т. п. — как рёбра. Применение различных вычислений, производимых на таком графе, позволяет спланировать оптимальный маршрут)

Теория графов содержит большое количество нерешенных проблем и пока не доказанных гипотез. Одной из таких проблем является проблема краевой раскраски графа – это назначение «цветов» рёбрам графа таким образом, что никакие два смежных ребра не имеют один и тот же цвет. Рёберная раскраска — это один из видов различных типов раскраски графов [1].

Постановка проблемы

Целью данной исследовательской работы является разработка автоматизированной системы краевой раскраски графа с применением различных алгоритмов обхода графа.

В теории графов раскраска ребер — это присвоение «цветов» ребрам графа, так что никакие два соседних ребра не имеют одного цвета. Это должно достигаться оптимальным (минимальным) количеством цветов.

Хроматическое число - наименьшее количество цветов, необходимое для окраски графа G [1]. Например, граф на рисунке 1 может быть окрашен минимум в 3 цвета.

Рисунок 1. Граф, раскрашенный тремя цветами

Два ребра называются смежными, если они связаны одной и той же вершиной [4]. Нет известного алгоритма полиномиального времени для окраски ребер каждого графа с оптимальным количеством цветов. Тем не менее, был разработан ряд алгоритмов, которые ослабляют один или несколько из этих критериев, они работают только на подмножестве графов, или они не всегда используют оптимальное количество цветов, или они не всегда работают в полиномиальное время.

Краевая раскраска графа является одним из нескольких различных типов задач раскраски графов. На приведенном ниже рисунке 2 показана раскраска ребер графика двумя цветами, в которых ни одно соседнее ребро не имеет одинакового цвета.

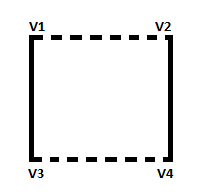
Рисунок 2. Граф, раскрашенный двумя цветами

Ниже приведен алгоритм решения задачи краевой раскраски графа. Данный алгоритм может отработать двумя способами. В первом способе для обхода графа используется алгоритм BFS (обход в ширину). Обход в ширину работает путём последовательного просмотра отдельных уровней графа, начиная с узла-источника U. Рассматриваются все ребра (U,V), выходящие из узла U. Если очередной узел V является целевым узлом, то поиск завершается; в противном случае узел V добавляется в очередь. После того, как будут проверены все рёбра, выходящие из узла U, из очереди извлекается следующий узел U, и процесс повторяется [3]. Во втором способе для обхода графа используется алгоритм DFS (обход в глубину). DFS описывается рекурсивно: перебираются все исходящие из рассматриваемой вершины рёбра. Если ребро ведёт в вершину, которая не была рассмотрена ранее, то запускается алгоритм от этой нерассмотренной вершины, а после происходит возврат и продолжение перебора рёбер. Возврат происходит в том случае, если в рассматриваемой вершине не осталось рёбер, которые ведут в нерассмотренную вершину. Если после завершения алгоритма не все вершины были рассмотрены, то необходимо запустить алгоритм от одной из нерассмотренных вершин [2].

Алгоритм:

1. Выбираем любую вершину и присваиваем разные цвета всем ребрам, связанным с ней, используя при этом уже имеющиеся цвета, если цветов не хватает добавляем новые. Отмечаем эти ребра как раскрашенные.

2. Переходим по одному из этих ребер.

3. Повторяем шаги с новым вершинами, пока все ребра не будут раскрашены.

         На рисунке 3 представлены входные данные, которые вводит пользователь.

Рисунок 3. Входные данные

На рисунке 4 показан исходный граф.

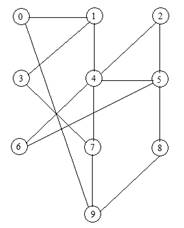
Рисунок 4. Исходный граф

На рисунке 5 представлены выходные данные, полученные в результате отработки алгоритма.

Рисунок 5. Выходные данные

На основе выходных данных можно построить графическое представление графа. Оно представлено на рисунке 6.

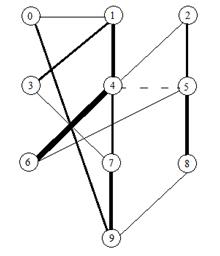
Рисунок 6. Раскрашенный граф

Пример реализации функции с использованием обхода в ширину.

// Функция для определения цвета ребра

Сравнение времени работы алгоритмов.

В таблице 1 показаны результаты сравнительного анализа зависимости времени работы алгоритмов от количества ребер.

Таблица 1.

Зависимость времени работы алгоритма от количества ребер

Заключение

В ходе проделанной работы был разработан алгоритм и реализована программа краевой раскраски графа, представлено графическое представление полученного графа, а также проведен анализ использованных алгоритмов. Анализируя результаты, можно сделать вывод, что алгоритм, использующий обход в ширину, работает быстрее алгоритма, использующего обход в глубину.