Использование алгоритмов теории графов для контроля территории

Введение В настоящий момент большое значение имеет обеспечение безопасности в местах большого скопления людей, а именно в метро, торговых центрах, школах, парках, местах культурного отдыха. Частично эту проблему можно решить, установив системы видеонаблюдения. Но как разместить камеры видеонаблюдения? Необходимо учесть множество факторов (географическое положение, количество проходящих людей, ценность расположенных в близи объектов, освещенность и т.д.) и при этом минимизировать затраты. Таким образом данную задачу можно рассматривать как задачу управления информационными и людскими потоками. Для ее решения необходимо найти минимальное число точек, в которых эффективно будет устанавливать камеры, то есть нужно найти минимальное число точек, связанных со всеми оставшимися, подобные вопросы в теории графов решают задачи о покрытии.

Но задача для например парка отдыха и многоуровнево здания будет различаться по сложности, поэтому интересно рассмотреть плоские и трехмерные модели территорий. Как учащийся школы я заинтересована в охране общеобразовательных учреждений, они относятся к трехмерным обьектам.   

Таким образом, цель работы:

Нахождение оптимального размещения средств визуального контроля территорий, представляемых в виде плоских и трехмерных моделей, с использованием алгоритмов теории графов.

Для достижения цели сформулируем ряд задач:

1. Изучить понятия доминирующих и независимых множеств вершин в графах;
2. Изучить алгоритмы нахождения доминирующих и независимых множеств вершин в графах и решения задачи о покрытии;
3. Изучить понятие планарности графа;
4. Разработать алгоритм для ее решения с использованием независимых и доминирующих множеств;
5. Подвести итоги

1. Основные понятия теории графов

Граф – абстрактная математическая модель, состоящая из множества вершин V, соединённых множеством рёбер E.

Пусть задан граф .

Если вершина V является концом ребра E, то говорят, что они инцидентны.

Если вершина v и ребро е инцидентны, то будем говорить, что вершина v покрывает ребро е, а ребро е покрывает вершину v.

Множество вершин, покрывающих все ребра графа, называется вершинным покрытием.

Независимое множество вершин – множество вершин графа, в котором никакие две вершины несмежны.

Доминирующее множество вершин   – множество вершин графа, в котором   каждая вершина  смежна с вершиной из .

Для нахождения максимальных независимых и минимальных доминирующих множеств вершин в графе можно использовать метод Магу.

Алгоритм Магу для нахождения независимых множеств

В ходе алгоритмы используются понятия математической логики: булева переменная, конъюктивная и дизъюнктивная нормальные формы, основные равносильности алгебры высказываний, которые известны из курса информатики.

Пусть задан граф ,  – его матрица смежности и S – максимальное независимое множество вершин.

С каждой вершиной графа  свяжем булеву переменную

Заметим, что если , то либо , либо , либо одновременно . А значит для всех , таких что  истинно высказывание . Учитывая конечность графа

Преобразуем правую часть выражения к дизъюнктивной нормальной форме с помощью основных равносильностей алгебры высказываний:

 - коммутативность;

 - идемпотентность;

 - дистрибутивность;

 – поглощение.

Получим

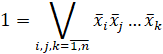
Данное высказывание истинно и позволяет сделать выводы о наборах вершин графа, не входящих одновременно в максимальные независимые множества вершин. Следовательно, получаем информацию о вершинах, образующих максимальные независимые множества.

Алгоритм Магу для нахождения доминирующих множеств Пусть теперь задан граф ,  – его матрица смежности и Т – минимальное доминирующее множество вершин. Тогда для произвольной вершины   должно выполняться одно из двух условий (или оба одновременно):

1) вершина  принадлежит множеству Т;

2) существует некоторая вершина , что  

Если с каждой вершиной связать булеву переменную

,

то будет справедливо высказывание

1=

Учитывая конечность графа

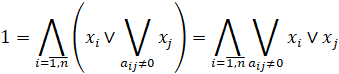
Преобразовывая правую часть к дизъюнктивной нормальной форме, получим информацию о минимальных доминирующих множествах графа.

2. Алгоритм нахождения покрывающих множеств

Исходя из последнего примера можно предложить следующий алгоритм для нахождения покрывающих множеств.

1. Найдем минимальные доминирующие множества;
2. Найдем минимальные независимые множества;
3. Если среди найденных доминирующих есть независимые, то задача решена;
4. Иначе, задача решается полным перебором всех возможных вариантов.

3. Понятие планарности графа

Плоский граф – это граф, который нарисован на плоскости так, что никакие два его ребра не пересекаются (рис.4). Планарный граф— граф, который может быть изображён на плоскости без пересечения рёбер. Иначе говоря, граф планарен, если он изоморфен некоторому плоскому графу, то есть графу, изображённому на плоскости так, что его вершины — это точки плоскости, а рёбра — непересекающиеся кривые на ней (рис. 3).

              

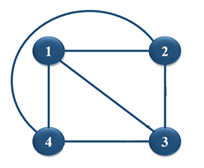
Рисунок 3. Планарный граф         Рисунок 4. Плоский граф

Непланарный граф не укладывается на плоскость. К непланарным относится полный граф с пятью вершинами (К₅ ) и граф «Домики и колодцы»()

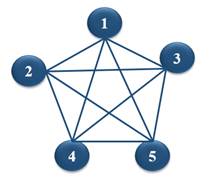
Рисунок 5. Полный граф с пятью вершинами      Рисунок 6. Граф «Домики и колодцы»

Теорема Понтрягина — Куратовского

Граф планарен тогда и только тогда, когда не содержит подграфов, стягивающихся в К₅ или  .

Заключение В ходе работы были проиллюстрированы базовые понятия и алгоритмы теории графов для нахождения независимых и доминирующих множеств вершин. Изучено понятие планарности графа, приведены примеры планарных и непланарных графов. А также примеры нахождения покрывающих множеств на графах, содержащих небольшое количество вершин.